【中1数学】中央値の求め方はこれでバッチリ！偶数・奇数の場合をそれぞれ解説！

今回は中１で学習する『資料の活用』という単元から

中央値の求め方について解説していきます。

高校生で学習するデータの分析という単元でもすっごく活躍する中央値、今のうちにしっかりとマスターしておきましょう！

中央値とは？？

データを大きい順に並べたとき、真ん中にある値を中央値といいます。

具体的にどういうことか説明していきますね。

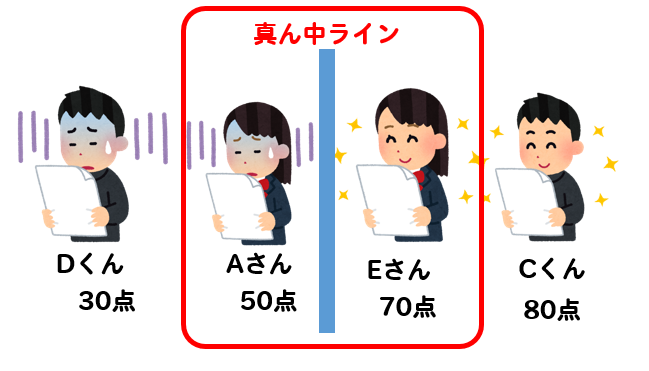
5人の生徒がテストを行った結果、以下のようになりました。

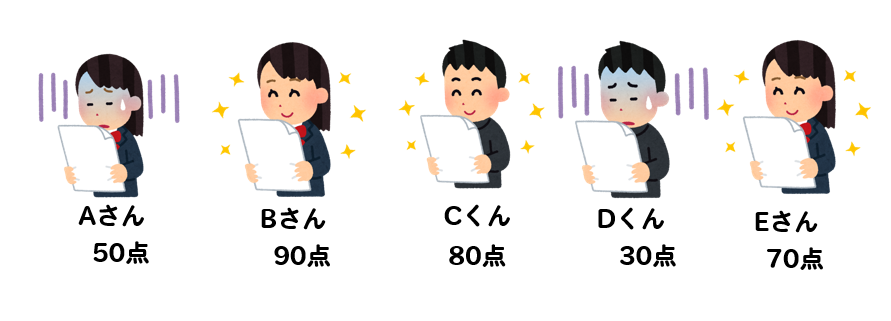
これを、点数の大きさ順に並びかえたところ

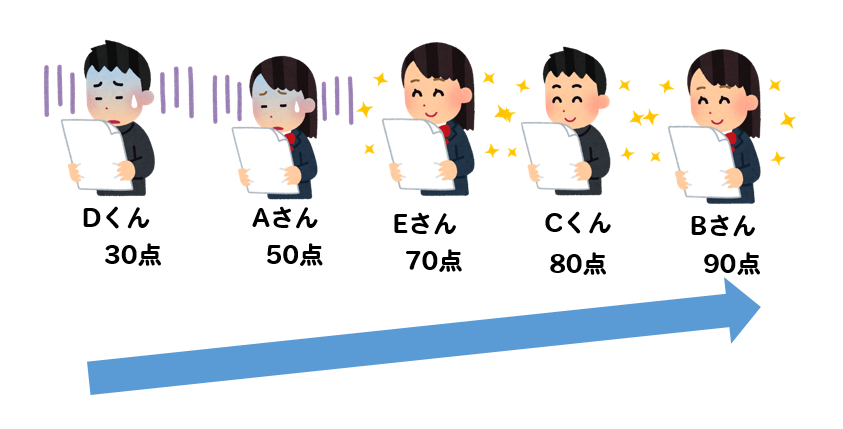
ちょうど真ん中に位置しているのは

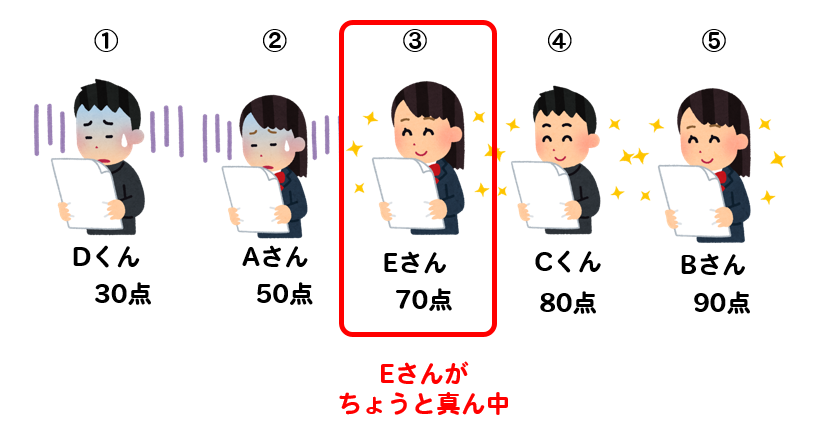
Eさんがちょうど真ん中に位置していることがわかりますね。

よって、Eさんの点数である70点が中央値となります。

このように、データを並び替えて

真ん中に位置する値のことを中央値といいます。

なるほど

とにかく真ん中にある値を見つければいいんだね！

簡単じゃーん！

たしかに簡単ですね！

だけど、この場合にはどうですか？

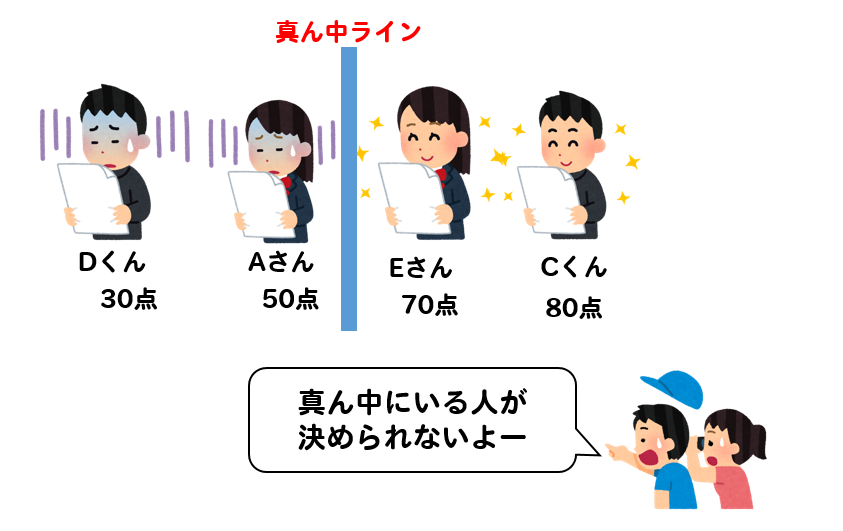
人数が偶数のときには、真ん中の値を決められないですよね！？

こういう場合には、どうやって中央値を求めれば良いのでしょうか。

人数が偶数のとき、奇数のとき

それぞれの場合においての中央値の求め方を解説していきます。

中央値の求め方（偶数）

データが偶数個あるときには、ちょうど真ん中に位置する値を見つけることができません。

この場合には、真ん中ラインを挟んでいる2つのデータを見て

それらの平均の値を中央値とします。

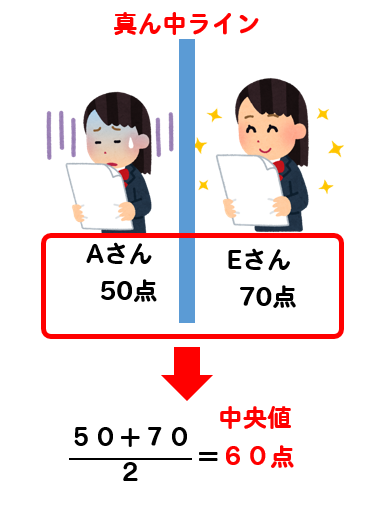
データの値が偶数個で、真ん中に位置する値を見つけれない場合には、

このように真ん中ラインを挟む2つのデータを見ることで中央値を求めていきましょう。

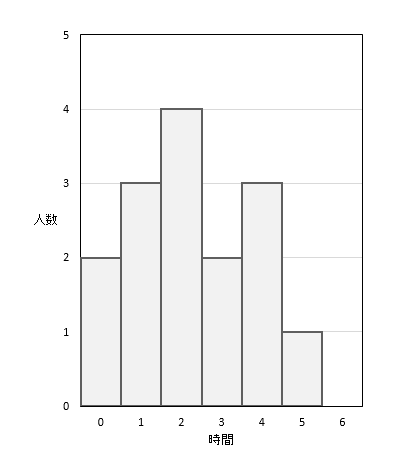
中央値は何番目？（偶数）

今回のようにデータが4個ある場合には、

2番目と3番目の平均を取れば良いということでしたが、

もしも、データが100個ある場合には、

何番目と何番目を見ていけば良いかわかりますか？？

正解は、50番目と51番目です！

どのように考えていけば良いかというと

データの数を2で割った数と

それに1を加えた数を見ていけば良いです。

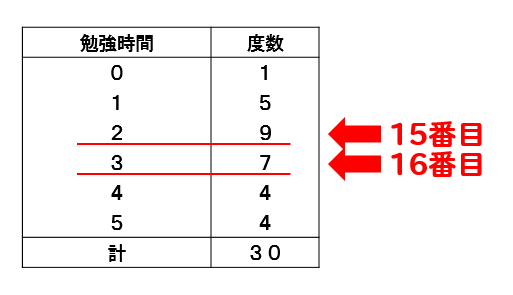
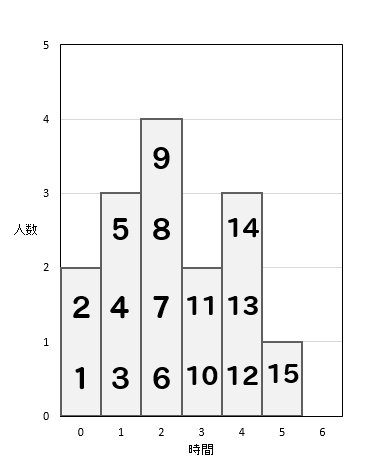
では、何番目のデータが中央値になるか調べる練習をしておきましょう。

このように、何番目のデータを見れば良いのかを理解しておけると、問題を解いていく上でとても役に立ちます(^^)

中央値の求め方（奇数）

データの数が奇数個の場合には、ちょうど真ん中に位置する値を見つけることができます。

そのため、真ん中に位置する値が何番目になっているのかを求めることができれば、すぐに中央値が分かりますね！

中央値は何番目？（奇数）

データが奇数個の場合には、

データの数を2で割った数を繰り上げた数を見ていけば良いです。

例えば、99個あるデータの中央値を求めたいときには

このように計算して、50番目のデータを見ていけば良いということになります。

では、何番目のデータが中央値になるか調べる練習をしておきましょう。

それでは、中央値の求め方が分かったところで実践問題に挑戦してみましょう。

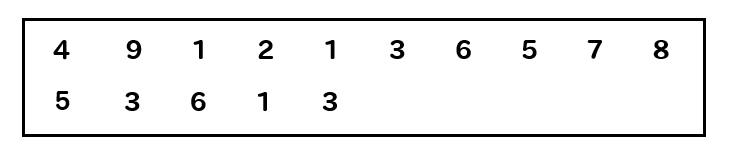
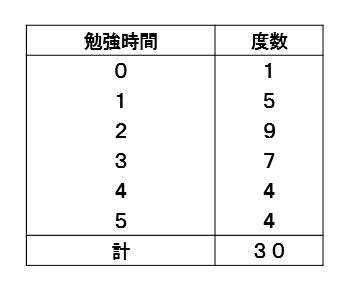
中央値を求める練習問題

下の資料は、生徒15人がテストを行ったときの点数を示したものである。この資料の中央値を求めなさい。

解説＆答えはこちら

答え

4点

 

全部で15のデータの中から中央値を求めるので

$$15\div 2=7.5$$

よって、データを大きさの順に並びかえたときの8番目の値が中央値となります。

下の表は、あるクラスの生徒全員について、自宅での勉強時間を表したものである。この資料の中央値を求めなさい。

解説＆答えはこちら

答え

2.5時間

全部で30のデータの中から中央値を求めるので

$$30\div 2=15$$

よって、データを大きさの順に並びかえたときの15と16番目の平均が中央値となります。

 

15番目の値は2時間

16番目の値は3時間であることがわかるので

$$\frac{2+3}{2}=2.5$$

よって、中央値は2.5時間となります。

下のヒストグラムは、あるクラスのある日の家庭学習を示したものである。この資料の中央値を求めなさい。

解説＆答えはこちら

答え

2時間

 

ヒストグラムの目盛りを読むと

全体で15のデータであることがわかります。

よって、中央値は8番目の値を見れば良いので

中央値は2時間となります。

中央値の求め方　まとめ

お疲れ様でした！

中央値を求めるときには

まず、何番目の値を見れば良いのかを判断しましょう。

データの総数が偶数の場合には

データの数を2で割った数と

それに1を加えた数を見ていきましょう。

データの総数が奇数の場合には

データの数を2で割って

繰り上げた数を見ていきましょう。

これで、たくさんのデータの中からでも

簡単に中央値を求めることができるようになりますね(^^)