高校数学Aで学習する平面図形の単元から
「三角形の内角、外角の二等分線と比」
について解説しておきます。
角の二等分線と比とは次のような性質のことをいいます。
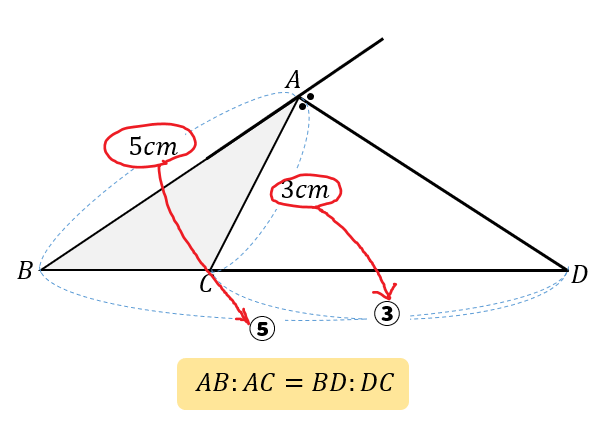
この性質をどのように利用するのか。
また、なぜこのような性質が成り立つのか。
サクッと確認しておきましょう(/・ω・)/
三角形の内角の二等分線と比
\(△ABC\)の\(∠A\)の二等分線は辺\(BC\)を\(AB:AC\)に内分する。
という性質があります。
イメージとしては屋根にあたる\(AB\)と\(AC\)の大きさの比は
床にあたる\(BD\)と\(DC\)の比と同じなんだよって感じだね。
屋根の比と床の比が同じ！
と覚えておきましょう(^^)
【問題】
次の図において、線分\(BD\)の大きさを求めなさい。
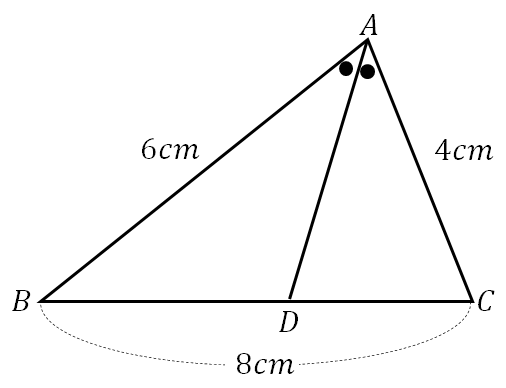
内角の二等分線の性質から
\(BD:DC=5:3\) であることが分かります。
すると、\(BC\)は\(5+3=⑧\)になると読み取れますね。
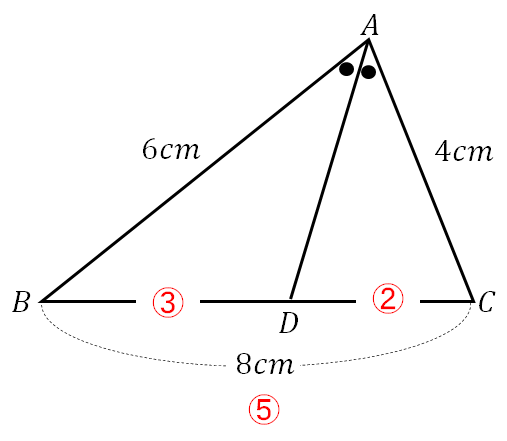
となると、\(BD\)というのは全体(\(BC\))を8個にわけた5個分であることが比から読み取れました。
よって
$$\begin{eqnarray}BD&=&BC \times \frac{5}{8}\\[5pt]&=&8\times \frac{5}{8}\\[5pt]&=&5\cdots(解) \end{eqnarray}$$
となりました。
証明は？
では、なぜ内角の二等分線と比にはこのような性質があるのか証明してみましょう。
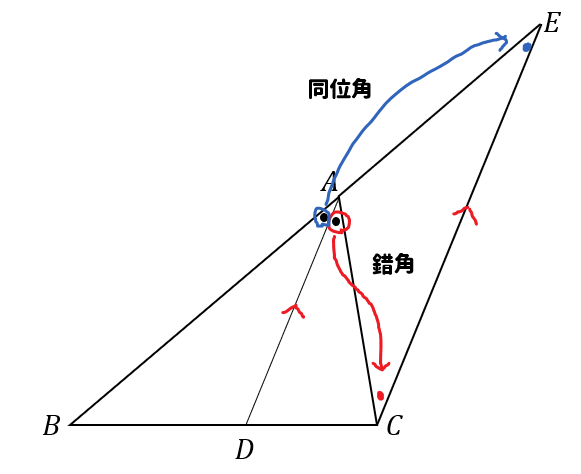
まず、辺\(AD\)と平行な線を点\(C\)を通るように引きます。
すると、図のように同位角、錯角により\(△ACE\)が二等辺三角形になることが分かります、
つまり、\(AC=AE\)となります。
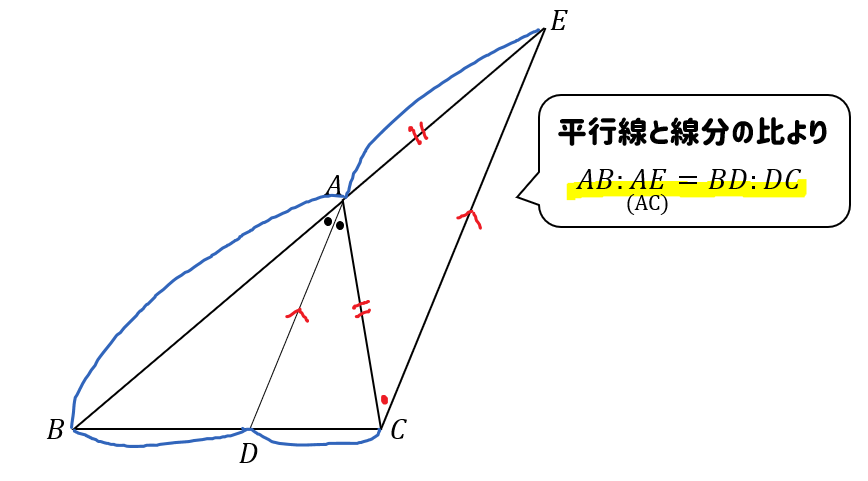
最後に、平行線と線分の比から
$$\begin{eqnarray}AB:AE(AC)=BD:DC \end{eqnarray}$$
となります。
平行線と線分の比とはこんなやつだね。
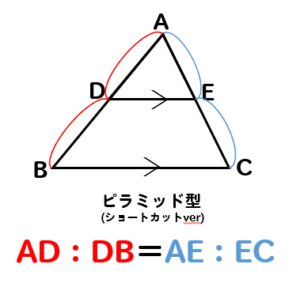
⇒ 【相似】平行線と比の利用、辺の長さを求める方法をまとめて問題解説！
三角形の外角の二等分線と比
\(△ABC\)の\(∠A\)の外角の二等分線と辺\(BC\)の延長との交点は辺\(BC\)を\(AB:AC\)に外分する。
という性質があります。
【問題】
次の図において、線分\(BD\)の大きさを求めなさい。
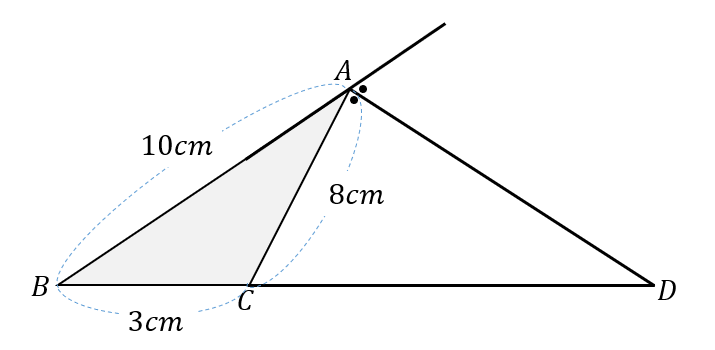
まず、外角の二等分線の性質から
\(BD:DC=10:8=5:4\) であることが分かります。
すると、\(BC\)は\(5-4=①\)になると読み取れますね。
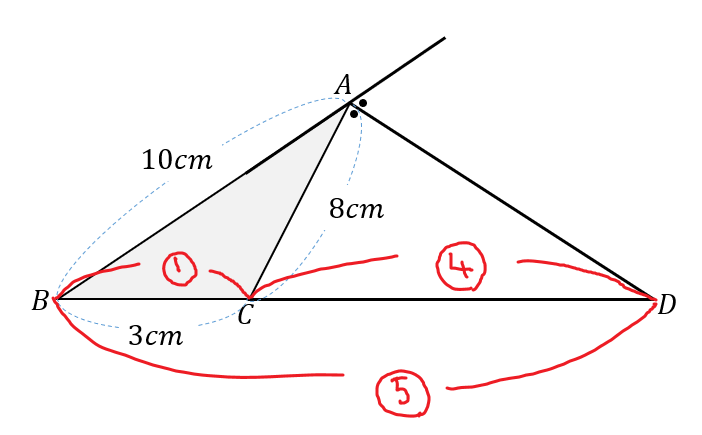
これによって、\(BC:BD=1:5\)であることが分かったので、\(BD=5BC\)。
$$BD=5BC=5\times 3=15\cdots(解)$$
となりました。
証明は？
では、外角の二等分線と比の証明を確認しておきましょう！
\(AB>AC\)の場合で考えてみましょう。
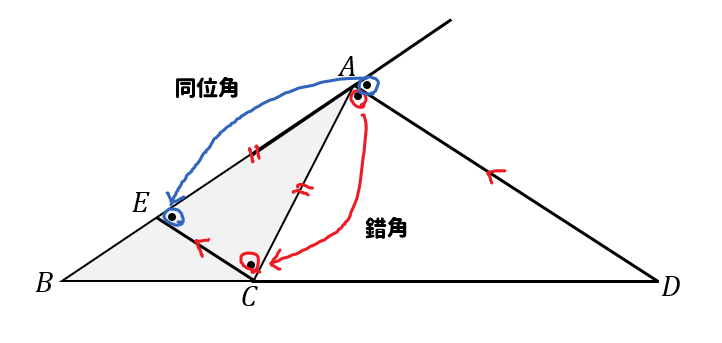
辺\(AD\)と平行な線を点\(C\)を通るように引き、辺\(EC\)とします。
すると、錯角、同位角が等しくなるので\(△AEC\)は二等辺三角形。
そして、\(AE=EC\)であることがわかります。
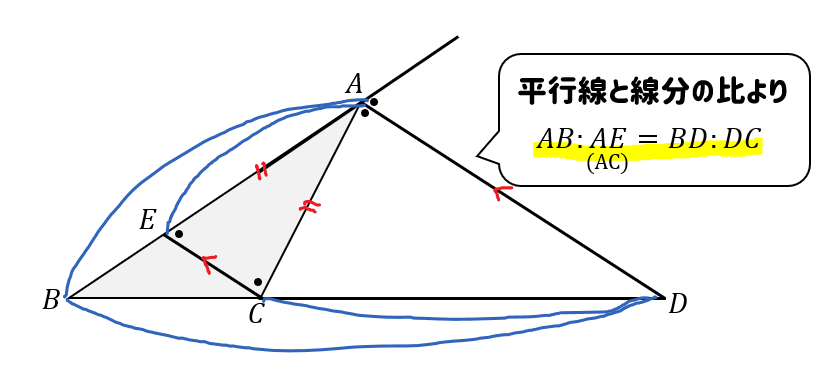
最後に、平行線と線分の比から
$$\begin{eqnarray}AB:AE(AC)=BD:DC \end{eqnarray}$$
となります。
まとめ！
お疲れ様でした！
内角の二等分線と比の性質は入試でもよく出題されます。
なので、絶対に覚えておきたいですね。
最後にそれぞれの特徴をもう1度確認しておきましょう(/・ω・)/
数スタの公式LINEを開設しました！