【一次関数】x軸上で交わる直線の式の求め方を解説！

一次関数の単元の中で

「\(x\)軸上で交わる直線の式を求めなさい」

という問題の解き方について解説します。

学校教科書の問いとして出題されていることもあって質問が多い1問です。

この記事を通してサクッと3分で理解しちゃいましょう！

x軸上で交わる直線の式は座標を求めることが大事！

解き方の手順は次の通り

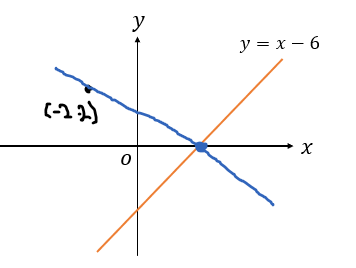
こんな感じです。

なので、まずは\(y=x-6\)と\(x\)軸との交点を求めましょう。

交点の求め方を忘れちゃった方はこちらで復習を！

⇒ 【一次関数】座標の求め方は？いろんな座標を求める問題について解説！

\(x\)軸との交点は、\(y=0\)を代入することで求めれましたね。

なので、\(y=x-6\)に\(y=0\)を代入すると…

$$\begin{eqnarray}0&=&x-6\\[5pt]6&=&x \end{eqnarray}$$

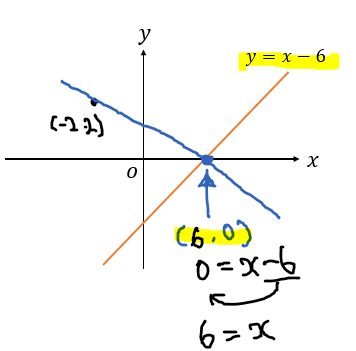
\(x\)軸との交点の座標は、\((6,0)\)となります。

これによって、求めたい直線の式は

\((-2,2)\)と\(6,0\)を通るってことが分かったので、あとは2点を通る直線の式の求め方をやればOKです。

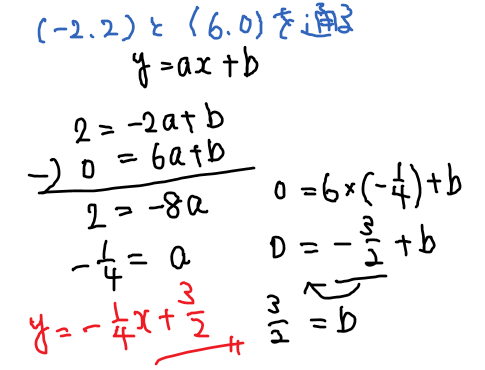
よって、答えは\(\color{red}{y=-\frac{1}{4}x+\frac{3}{2}}\)となります。

ちなみに今回の問題は、こちらの動画でも解説しています(/・ω・)/

まとめ！

「\(x\)軸上で交わる直線」という問題は

まず、\(y=0\)を代入して\(x\)軸との交点を求める。

そして、その座標を用いて2点を通る直線の式を求めるやり方でやっていけばOK！

難しそうに見えた問題だけど

実際には楽勝だね！

これでテストも得点アップ間違いなし！

ファイトだ(/・ω・)/