【1次関数】みんなニガテな動点の問題のコツを伝授！

今回は中2で学習する一次関数の単元から

「一次関数の利用（動点）」

についてイチから解説していきます。

取り上げる問題はこちら！

【動点の問題】

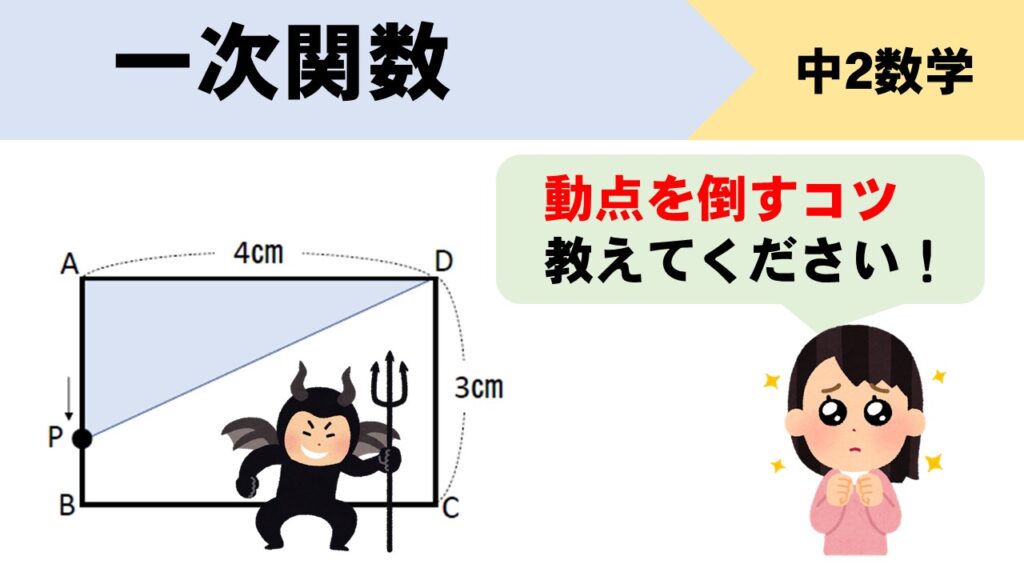
下の図のような長方形ABCDで、点PはAを出発して秒速1㎝で辺AB、BC、CD上をDまで動く。点PがAを出発してから\(x\)秒後の△APDの面積を\(y\)㎠とする。次の問いに答えなさい。

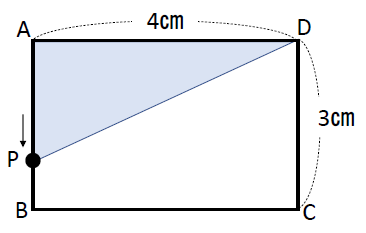
（1）点Pが次の場合、\(y\)を\(x\)の式で表しなさい。また、\(x\)の変域も求めなさい。

① AB上にある　　② BC上にある　　③ CD上にある

（2）\(x,y\) の関係をグラフに表しなさい。

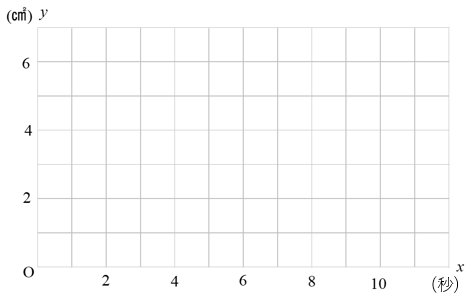
（3）△APDの面積が4㎠になるのは、点PがAを出発してから何秒後か求めなさい。

動点を苦手にしている人は多いんだけど、ちゃんとコツを身につければ簡単に解けるようになるよ＾＾

今回は理解を深めるための動画講義もつけているので、あわせてご活用ください！

動点の解き方のポイント！

まず最初に動点のポイントをお伝えしておきます。

ポイント①　点がある場所をイメージ図でかく！

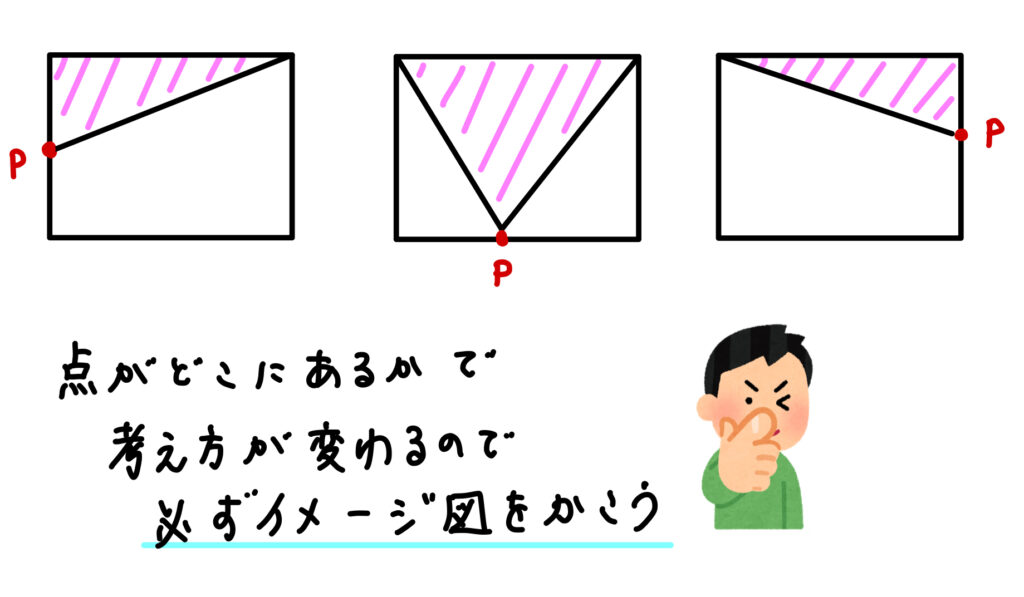
このように、点がどの場所にいるのかをわかりやすくするためイメージ図をかくようにしてください。

頭の中だけでやろうとすると難しくなってしまうので、イメージ図を見ながら考えるようにしましょう＾＾

ポイント② 出発地点から動点が今いるところまでの長さを\(x\)で表す。

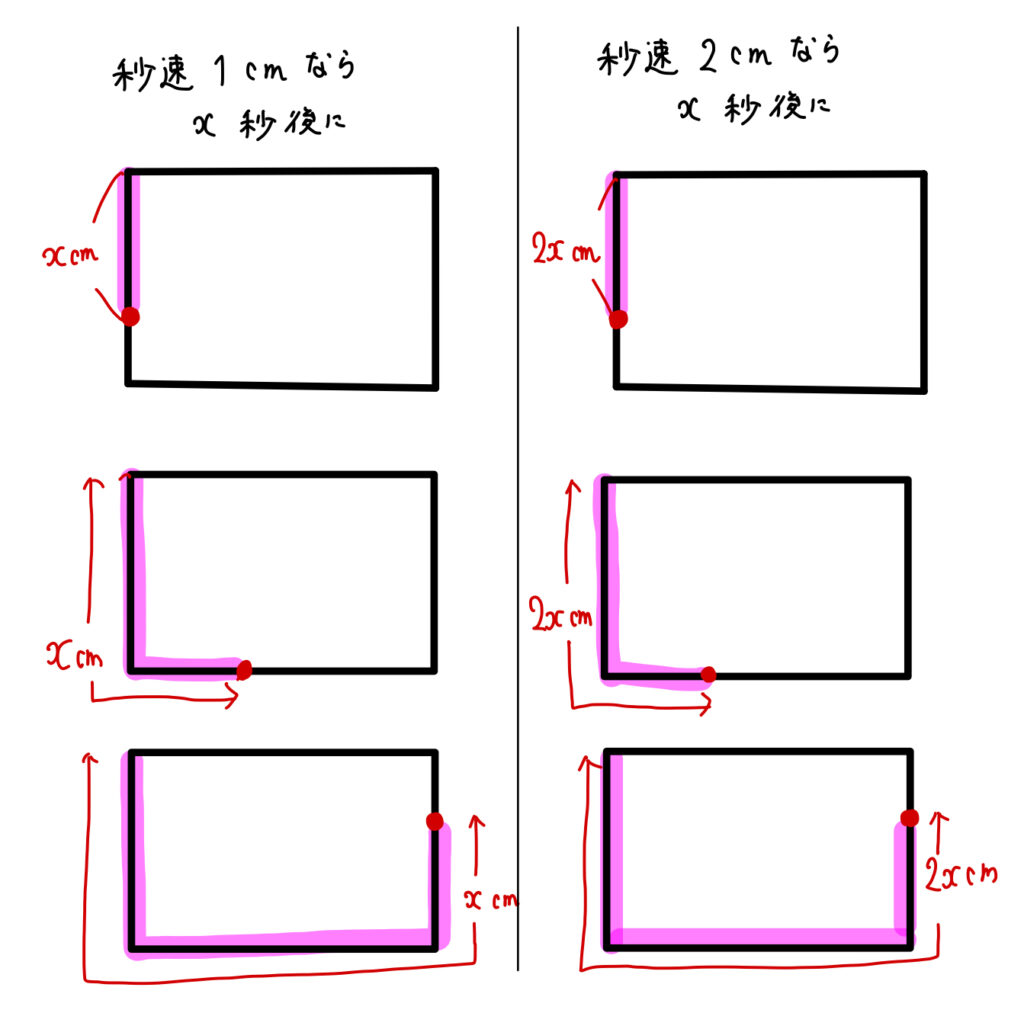
この2点をおさえておけば動点の問題は楽勝だよ＾＾

（1）式のつくり方の解説

まずは①AB上にあるときのイメージ図を書いて、出発地点のAからPまでの長さを\(x\)で表しましょう。

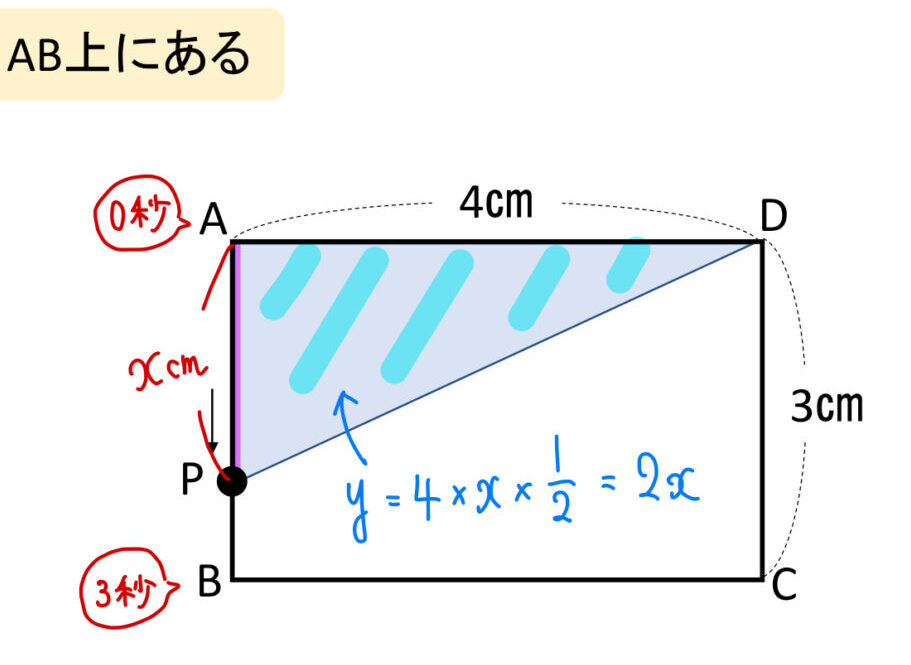
すると、△APDの面積は \(（底辺）\times（高さ）\times \frac{1}{2}\) で求めることができるので

$$y=2x$$

と式を作ることができますね！

変域については出発地点（A）からゴール地点（B）までにかかる時間を考えればOKです。

1秒に1㎝ずつ進むのだから、点Bに到達するには \(3\div 1=3 \)秒だとわかります。

よって、AB上を動くときは0秒から3秒なので \(0≦x≦3\)となります。

次にBC上にある場合を考えましょう。ここでもイメージ図を活用して長さを書き込むのですが

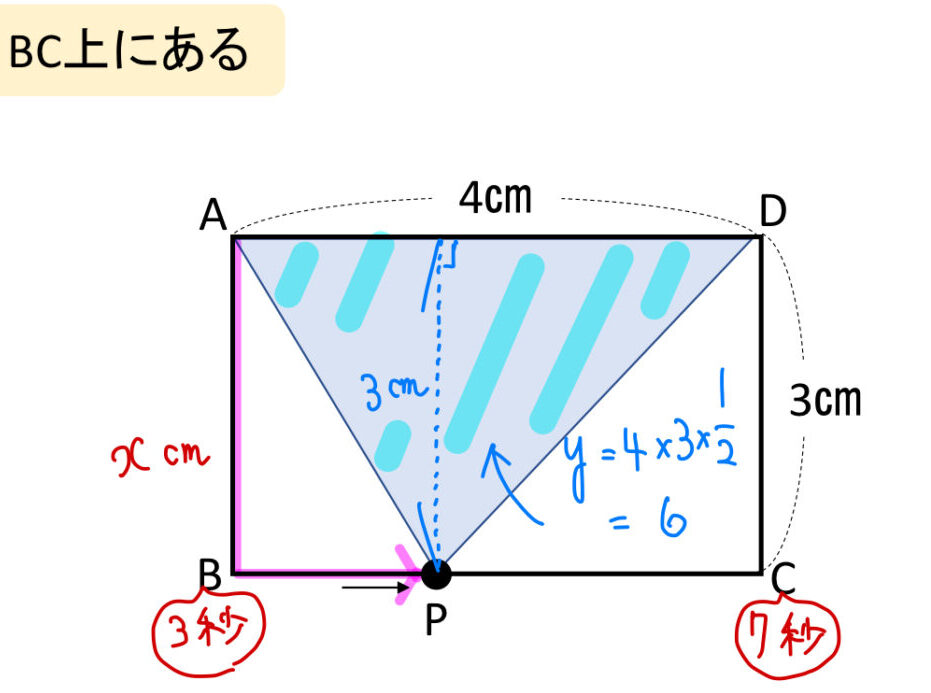
この図においては、△APDの面積を求めるのに\(x\)の長さは不要です。

常に「底辺4㎝、高さ3㎝」となっているので、面積は \(y=6 \)となります。

また、点Bの地点では3秒でしたが、Cに到達するまでに4秒かかるのでC地点では7秒となります。

よって、変域は\(3≦x≦7\)となりますね！

最後にCD上にある場合を考えていきましょう。

ここがちょっとやっかいです(^^;)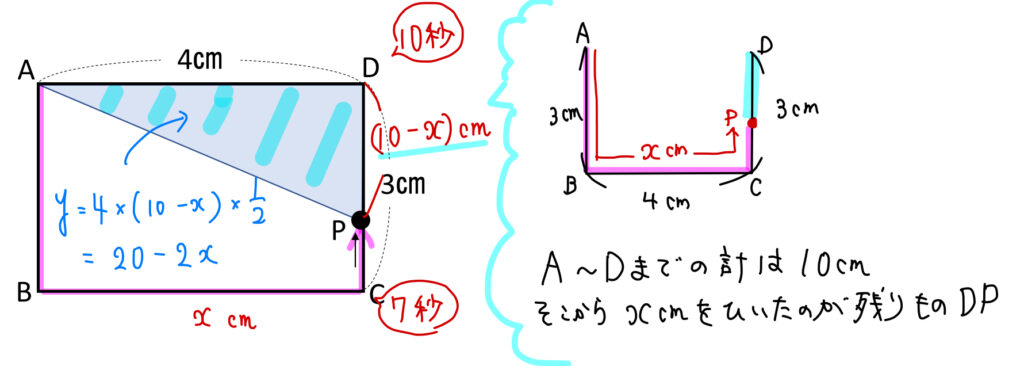△APDの面積を表すためには、辺DPの長さが必要になります。

この部分は、図で説明している通りA～Dまでの長さの合計からA～Pまでの長さ\(x\)cmを取り除くことで表せます。よって、\(DP=10-x \)となりますね。

ここが乗り越えられるかどうかが動点最大のポイントかもしれません(._.)

そうすれば面積は、\(y=4\times (10-x)\times \frac{1}{2}=20-2x\) となります。

また、変域についてはC地点で7秒、そこからDに到達するまでに3秒かかるのでD地点では10秒ですね。

よって変域は、変域は\(7≦x≦10\)となります。

③が理解しにくい…という方は解説動画で考え方をインプットしてください！

（2）グラフのかき方の解説

（1）で作った式と変域をもとに次のようにグラフを完成させます。

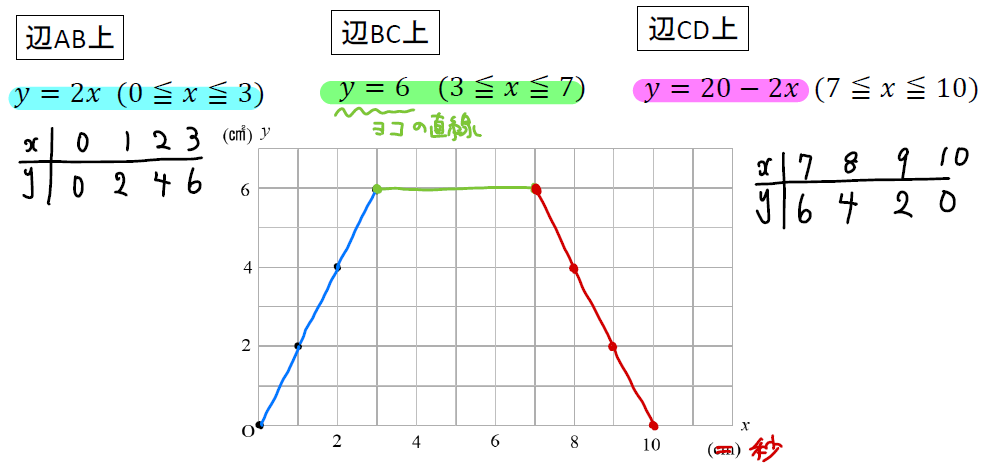
最初は\(y=2x\)のグラフを\(x\)が0～3の範囲でかきます。

切片0、傾き2のグラフなので原点から出発して2ずつ増えていくようにかけばOKですね。

もしくは、図にあるように対応表をつくって1つずつ点をとっていくやり方でもOK！この方がシンプルでかきやすいかもです＾＾

次は\(y=6\)のグラフですが、これは真横の直線になります。

\(y\)座標が6のところに、\(x\)が3～7までの範囲で横線を入れていきましょう。

最後に\(y=20-2x\)のグラフです。

これは図のように対応表をつくって、1つずつ点をとってみるとグラフがかきやすいです！

3つのグラフをかき終えたら完成ですね(‘◇’)ゞ

基本的にすべてのグラフはつながった形になります。

もしも、グラフがつながらずにバラバラになってしまったら（1）の式が間違っている可能性があるので見直してみてください！

（3）何秒後か？の解説

（2）でつくったグラフを利用すれば楽勝です！

面積が4㎠になる。つまり、\(y=4\)になる点をチェックしていきましょう。

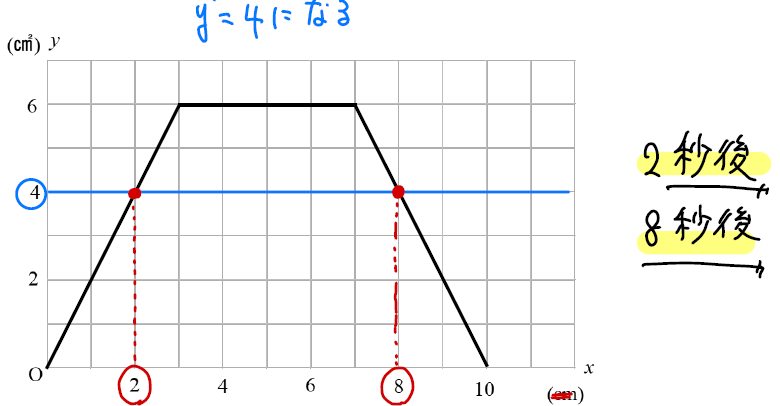
すると、このように2秒後、8秒後というのが読み取れますね！

ちょっと難易度が高い問題では、\(x\)の目盛りがぴったり読み取れない場合もあります。

そのときは、（1）で作った式に\(y=4\)を代入して、方程式を解いて\(x\)の値を求めるようにしてください。

まとめ！

お疲れ様でした！

動点の問題は理解できましたか？？

最初に説明した2つのポイントがありましたね。

ポイント①　点がある場所をイメージ図でかく！

ポイント② 出発地点から動点が今いるところまでの長さを\(x\)で表す。

この2つはものすごく重要なので、動点を解くときには必ず思い出すようにしてくださいね＾＾