高校数学Ⅰで学習する内容から
「絶対値記号の外し方」
について解説していきます。
絶対値の外し方のポイントは単純です。
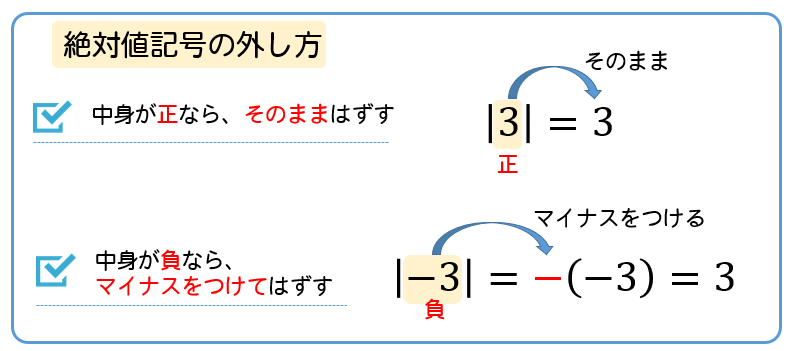
中身が正なら、そのまま。
中身が負なら、マイナスをつけてはずす。
もしも絶対値の中身の正負が判断できない場合

このように2パターンに場合分けをしていくことになります。
では、問題を見ながら絶対値の外し方について確認していきましょう!
今回の記事はこちらの動画でも解説しています(/・ω・)/
【基本編】
【応用編】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
絶対値記号の外し方【基本】
【問題】
次の値をそれぞれ求めよ。
(1)\(|-6|\)
(2)\(|3-\pi|\)
(3)\(|\sqrt{2}-1|\)
絶対値の中身が正ならそのまま。
絶対値の中身が負ならマイナスつける。
この基本に沿って考えていけばOKです。
(1)

これは簡単ですね!
絶対値の中身\(-6\)は負の数なので、マイナスをつけて外していきましょう。
(2)

\(3-\pi\)って、パッと見では正に見えませんか??
だけど、\(\pi=3.14\cdots\) であることを思い出してもらえると、
\(3-\pi=3-3.14\cdots =-0.14\cdots\)
となり、負の数であることが分かりますね。
絶対値では、\(\pi\)を使った問題がよく出題されるので覚えておきましょう。
(3)
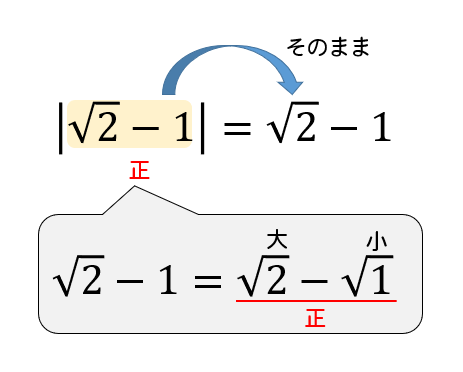
ルートが付いていると正負の判断がつきにくいですね。
この場合には、整数をルートの形にすることで正負の判断がつきやすくなります。
また、ルートの近似値を覚えておくというやり方もあります。
\(\sqrt{2}=1.4142\cdots\) 、\(\sqrt{3}=1.732\cdots\)
練習問題
【問題】
次の値をそれぞれ求めよ。
(1)\(|6-4\sqrt{2}|\)
(2)\(|3\pi-10|\)
絶対値記号の外し方【場合分け】
【問題】
次の式の絶対値記号を\(x\)の値によって場合分けしてはずせ。
(1)\(|x-2|\)
(2)\(|2x+4|\)
絶対値の中身に文字が入っていて、
符号が決められないときには、場合分けをしていきましょう。
(1)
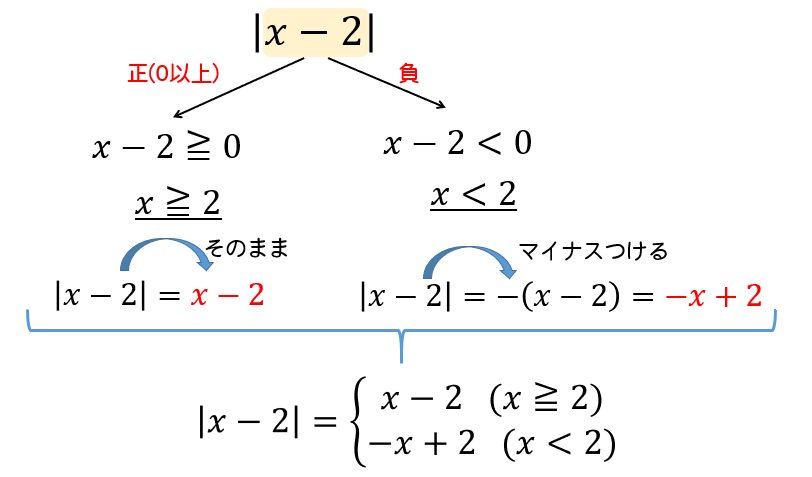
絶対値の中身 \(x-2\) に注目。
\(x-2\) が正(0以上)になるとき
\(x-2≧0\) ⇒ \(x≧2\) のときには、絶対値はそのままはずせるので
\(|x-2|=x-2\) となります。
\(x-2\) が負になるとき
\(x-2<0\) ⇒ \(x<2\) のときには、絶対値はマイナスをつけてはずすので
\(|x-2|=-(x-2)=-x+2\) となります。
これらをまとめると次のように表せます。
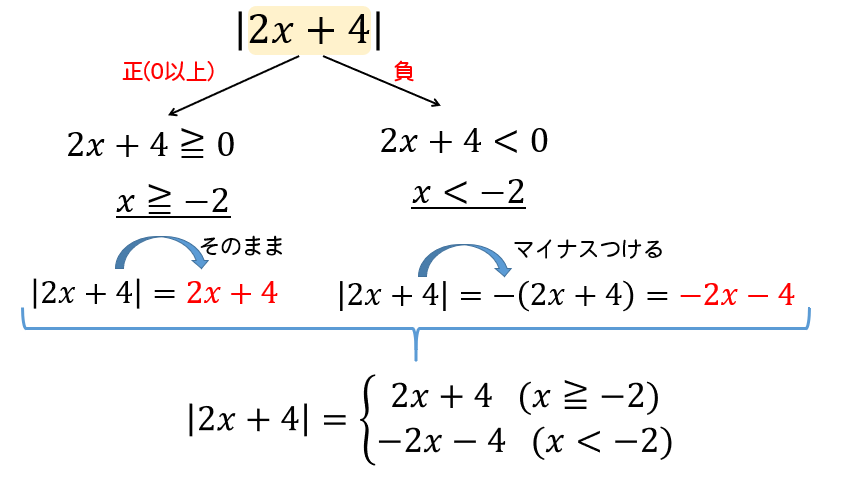
(2)
こちらも(1)と同じように考えていけばOKです。
練習問題
【問題】
次の式の絶対値記号を\(x\)の値によって場合分けしてはずせ。
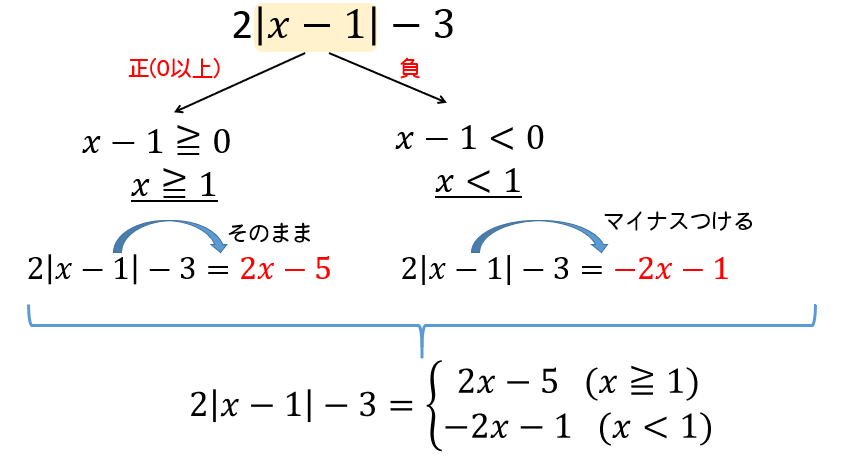
$$2|x-1|-3$$
絶対値記号の外し方【2つ】
【問題】
次の式の絶対値記号をはずして表せ。
$$|x+2|+|x-1|$$
絶対値が2つ以上になってきたときには、ちょっとだけ場合分けが複雑になります。
ですが、考え方は単純!
それぞれの絶対値での場合分けを組み合わせて考えていけばOKです。
まず、\(|x+2|\)の場合分けを考えると、
$$\begin{eqnarray}|x+2|=\begin{cases}x+2 & ( x ≧ -2 ) \\-x-2 & ( x < 2 )\end{cases}\end{eqnarray}$$
となります。
次に、\(|x-1|\)の場合分けを考えると、
$$\begin{eqnarray}|x-1|=\begin{cases}x-1 & ( x ≧ 1 ) \\-x+1 & ( x < 1 )\end{cases}\end{eqnarray}$$
となります。
これらの場合分けを1つの数直線上にまとめてみると、
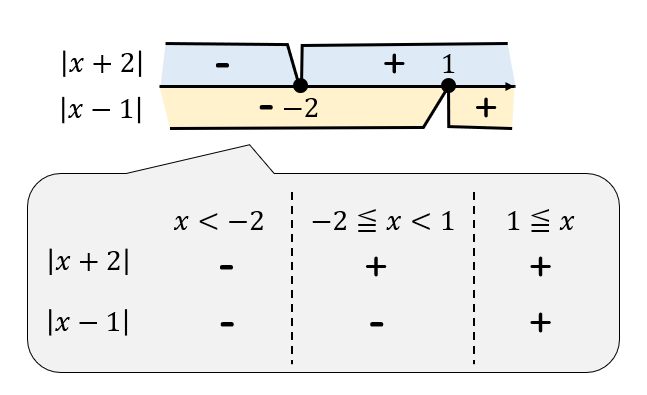
このように、3つのパターンがあると分かりますね。
今までは絶対値が1つだったので、それが正or負の2パターンでしたが、
絶対値が複数になると、負と負、正と負、正と正など
様々なパターンが考えられるようになります。
では、この3つのパターンにわけて絶対値をはずしていきましょう。
\(x<-2\) のとき
\(|x+2|=-x-2\)、\(|x-1|=-x+1\) だから
$$\begin{eqnarray}|x+2|+|x-1|&=&-x-2-x+1\\[5pt]&=&-2x-1 \end{eqnarray}$$
\(-2≦x<1\) のとき
\(|x+2|=x+2\)、\(|x-1|=-x+1\) だから
$$\begin{eqnarray}|x+2|+|x-1|&=&x+2-x+1\\[5pt]&=&3 \end{eqnarray}$$
\(1≦x\) のとき
\(|x+2|=x+2\)、\(|x-1|=x-1\) だから
$$\begin{eqnarray}|x+2|+|x-1|&=&x+2+x-1\\[5pt]&=&2x+1 \end{eqnarray}$$
以上のことをまとめると
$$\begin{eqnarray}|x+2|+|x-1|=\begin{cases}-2x-1 & ( x < -2 ) \\3 & ( -2≦x <1 )\\2x+1&(x≧1)\end{cases}\end{eqnarray}$$
となります。
絶対値が複数ある場合には、それぞれの場合分けをして、
1つの数直線上にまとめて考えるというのがポイントですね!
練習問題
【問題】
次の式の絶対値記号をはずして表せ。
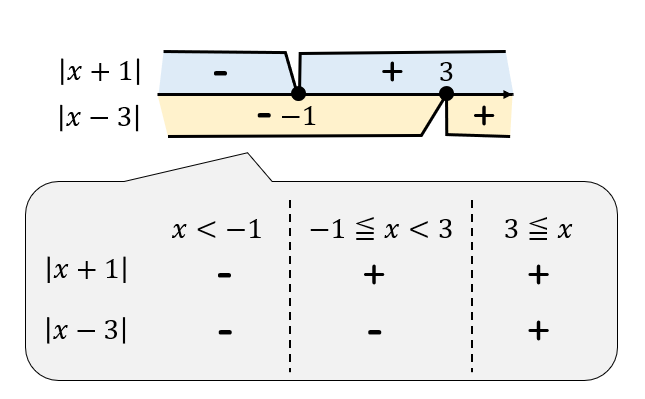
$$|x+1|+|x-3|$$
まとめ!
お疲れ様でした!
絶対値の外し方について基礎から応用まで紹介しました。
ですが、考え方は1つ。
絶対値の中身が正なら、そのまま。
絶対値の中身が負なら、マイナスつける。
これをおさえておけば大丈夫でしょう(^^)
絶対値の外し方を理解したら、
次は絶対値の方程式、不等式ですね!
ぜひ、こちらの問題にも挑戦してみてくださいね(/・ω・)/


















何見て分からなかったのに一発で理解できました!!
なぜ3つで場合分けなのかずっと疑問に思ってましたが、図での解説がとても分かりやすかったです。
本当にありがとうございます。
お役に立てて嬉しいです^^
ちょっと面倒だけど、図をかいて考えると理解しやすいよね!