今回は、小学生の算数で学習する
『つるかめ算』の計算方法から
中学入試に出題されるような応用問題の解説をおこなっていくよ！
つるかめ算の基本問題と解き方については
こちらの記事を参考にしてみてくださいね(^^)
＞＞＞つるかめ算の基本問題と解き方を１からていねいにやってみよう！
３つのつるかめ算、考え方は？
今回取り上げるのは、３つの数量がでてくる問題だ！
問題
ツルとカメとカブトムシが合わせて33匹います。
足の数の合計は148本でした。
ツルの数はカメの数の2倍のとき、それぞれの数が何匹ずつになるか求めなさい。
※めんどうだから、すべて匹で数えさせてねｗ
ツル、カメ、カブトムシ
登場キャラクターが３つもいる！
こうなってくると
ちょっと厄介だ！
３つもキャラクターが登場するときには、ちょっとしたコツが必要になる。
手順は以下の通りだ。
- 全部が〇〇だとしたら…
- 残り2つを1セットにする
- 取り替えていく
手順① 全部が〇〇だとしたら
これは、つるかめ算の基本問題と同じ
全部がカブトムシだとしたら！
これで話を進めていきましょう。
全部がカブトムシ
つまり、カブトムシが33匹いた場合を考えると
足の数は198本となり
148本を50本もオーバーしたことになります。
ここから50本分を取り換えて減らしていきましょう。
手順② 残り２つを1セットにする
ツルの数は、カメの数の2倍ということだから
カメが１匹いれば、ツルは二倍の2匹いるということになりますね。
カメが2匹いれば、ツルは4匹
カメが3匹いれば、ツルは6匹…
このように増えていくはずです。
だから、カメ1匹とツル2匹を1セットにして考えていきましょう。
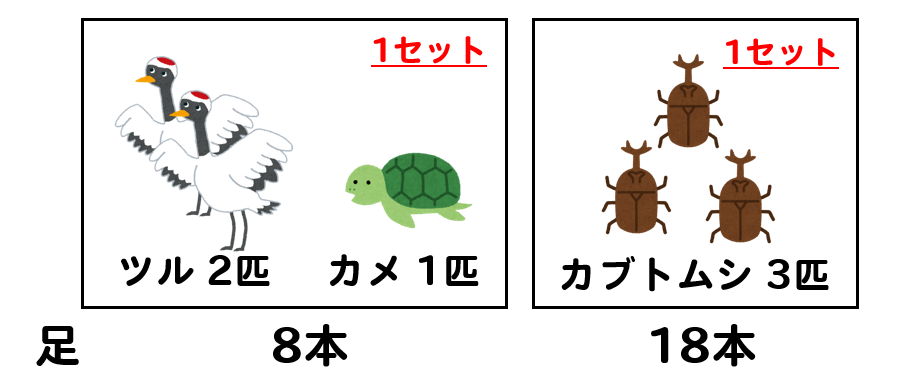
同様にカブトムシも3匹で1セットを作ります。
すると、それぞれの足の本数は
ツルカメセットが8本
カブトムシセットが18本となります。
手順③ 取り替えていく
手順②で作ったセットを取り替えていきます。
カブトムシ1セットを減らして
ツルカメ1セットを増やすと
$$18-8=10本$$
足の数は、10本減ったことになります。
全体で50本分の足を減らしたいので
$$50\div 10=5$$
5セット分を取り換えればOKだということがわかりますね！
つまり
ツルは、\(2\times 5=10匹\)
カメは、\(1\times 5=5匹\)
カブトムシは、\(3\times 5=15匹\)減らしているから\(33-15=18匹\)となります。
答え
ツル…10匹
カメ…5匹
カブトムシ…18匹
3つのキャラクターが登場したときには
こんな感じで問題の条件に合わせて
セットを作ってあげることが大事なポイントだね！
それでは、この手順を用いて
3つのつるかめ算を練習してみよう！
練習問題で理解を深めよう！
2本足のイスと3歩足のイスと4本足のイスが、合わせて43個あります。足の数は合わせて122本です。
2本足のイスと3本足のイスの数の比を\(9:7\)にしました。このとき、4本足のイスはいくつか求めなさい。
まとめ
お疲れ様でした！
3つのつるかめ算は、かなり応用が利いていて難しいです(^^;
だけど、今回紹介したような手順を
キチンとたどることができれば答えを出すことはできますね！
手順が身についたら、あとは練習あるのみ！
問題集や入試過去問を使ってどんどん練習していこう(/・ω・)/
とても解説がわかりやすいです