【三角形の面積公式】小学生はどうやって解く？問題を使って解説！

小学生で学習する単元

「三角形の面積」

について解説していくよ！

 

三角形の面積公式とは？

なんでこうやって求めるんだっけ？

実際に問題を解いてみよう！

という流れでお話を進めていきますね(^^)

 

三角形の面積公式

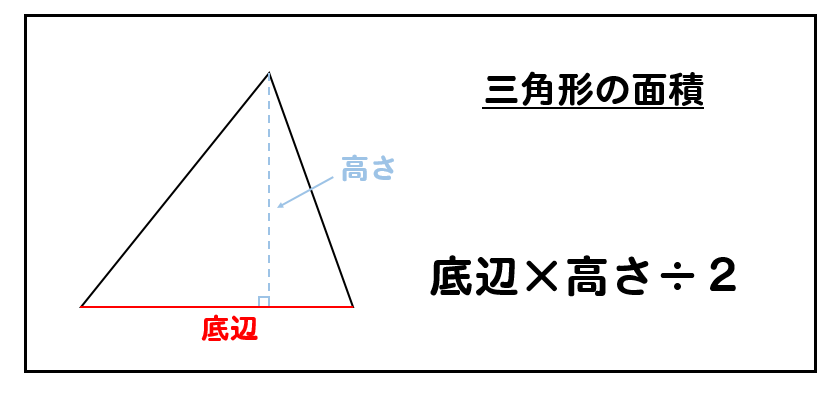
三角形の面積は、このように求めることができます(^^)

公式自体はとっても簡単ですね。

 

だけど、注意しておきたいのは…

底辺と高さの場所になります。

 

底辺となる辺は自由に選ぶことができます。

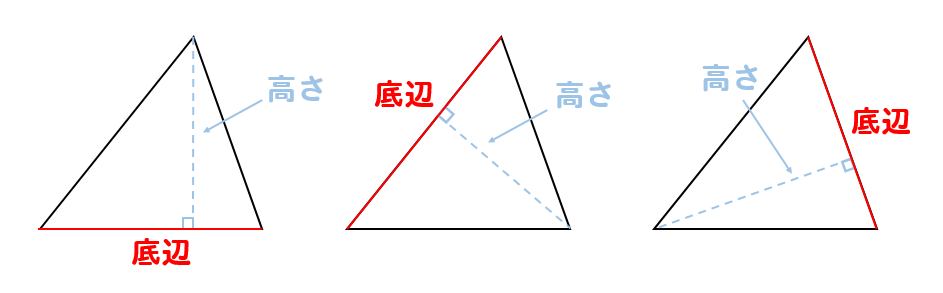
このように、どの辺を選んでもOK！

ただし、どこを底辺に選ぶかによって高さの位置も変わってくるので注意ですね。

 

 

高さとは、底辺の向かいにある頂点からまっすぐに下した辺のことです。

 

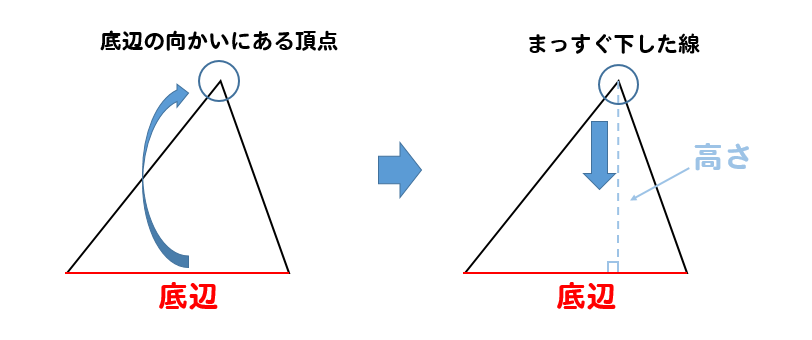
なので、こういった変わった形のとき

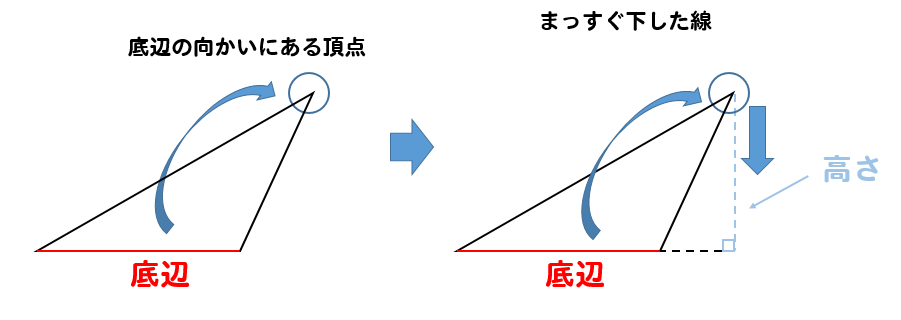
このように、三角形からはみ出した場所になってしまうので気を付けておきましょう。

 

なぜ２で割るの？

さて、三角形の面積公式はシンプルなモノでしたね。

だけど、ここで疑問に感じちゃうことが…

なんで２で割るの！？

 

実際に、多くの子どもたちが三角形の面積を求めるとき

この÷２を忘れてしまいます…

 

なぜ２で割る必要があるのか？

このことを理解しておけば、÷２を忘れてしまうことはないでしょう！

 

三角形ってね

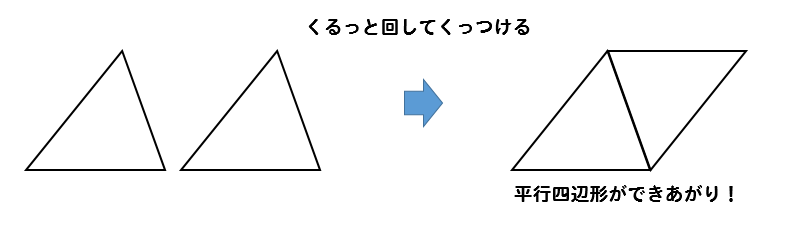
こうやって２つ重ねると、平行四辺形を作ることができるんだよね！

 

だから、三角形の面積を求めたければ

２つくっつけて平行四辺形の面積を求める。

そして、それを半分にする！

という考え方を用いているのです。

 

 

平行四辺形の面積が

（底辺）×（高さ）

で求めれることを思い出してもらうと

三角形の面積公式は、このように考えることができますね。

 

 

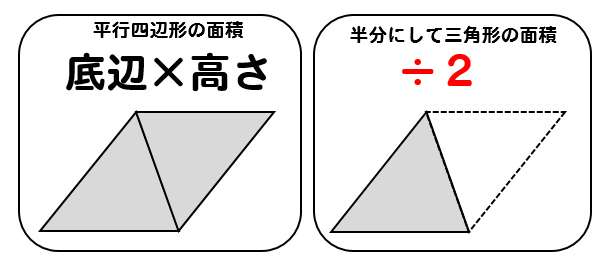
三角形の面積を求めるためには

一旦、平行四辺形の面積を求め

それを半分にしている。

だから、２で割る必要があるんですね！

 

忘れないように覚えておきましょう(^^)

三角形の面積を求める問題

それでは、三角形の面積公式を使って問題を解いていきましょう。

三角形の面積基本問題

 

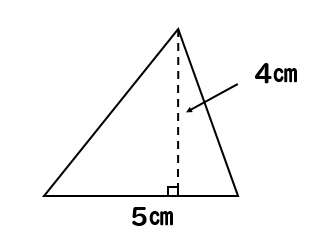
この三角形では、底辺が5㎝、高さを4㎝と見ることができますね。

よって

$$\Large{5\times 4\div2=10(cm^2)}$$

となりました。

 

公式を覚えていれば簡単な問題ですね！

どこを見ればいい！？

次は、どこを底辺と高さにすればいいのか悩んでしまう問題です。

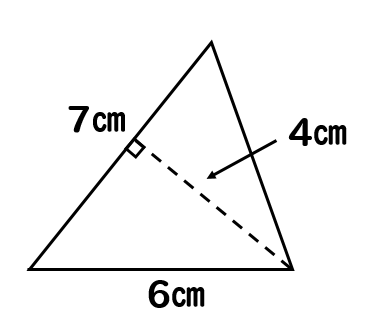
この問題では、どこを底辺、高さとして見ていけばよいでしょうか？

 

6㎝の部分を底辺と考えた場合

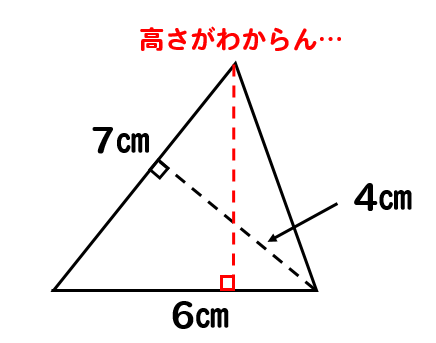
高さに当たる部分の長さが分かりません…

これでは公式に当てはめることができませんね。

 

というわけで、今回の問題では

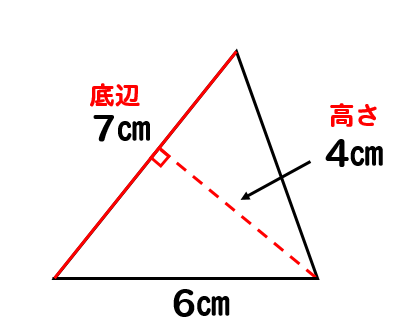
底辺を7㎝、高さを4㎝として考えていきましょう。

6㎝という辺の長さは面積を求めるためには不要な情報です。

引っかからないよう気を付けてくださいね(^^;

 

以上より、三角形の面積は

$$\Large{7\times 4\div2=14(cm^2)}$$

となりました。

 

どこが高さ！？

どこを高さに選べばいいの！？という問題を見ておきましょう。

 

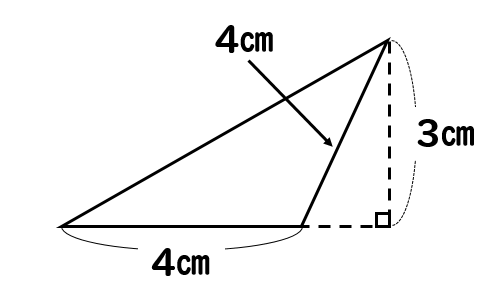
今回のような三角形では、図形からはみ出した部分になってしまいますが

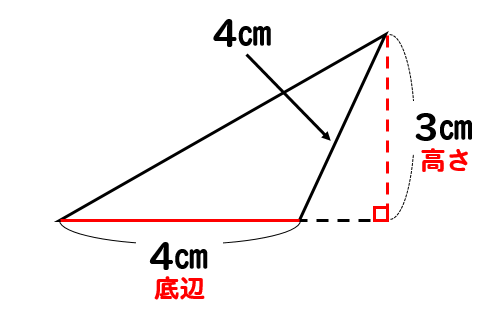
ここの部分が底辺と高さになりますね。

 

よって、三角形の面積は

$$\Large{4\times 3\div2=6(cm^2)}$$

となりました。

 

三角形が２つくっついている！？

次の図形は四角形になるんだけど、三角形の面積を利用して解いていきます。

 

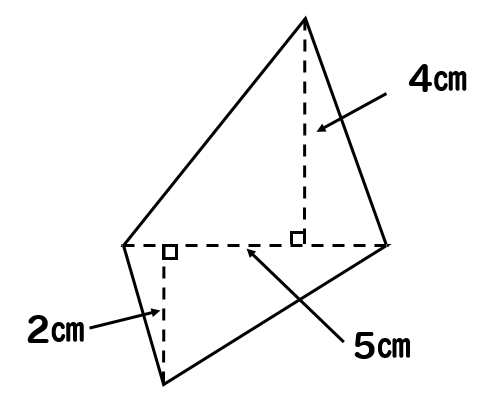
このような四角形の場合

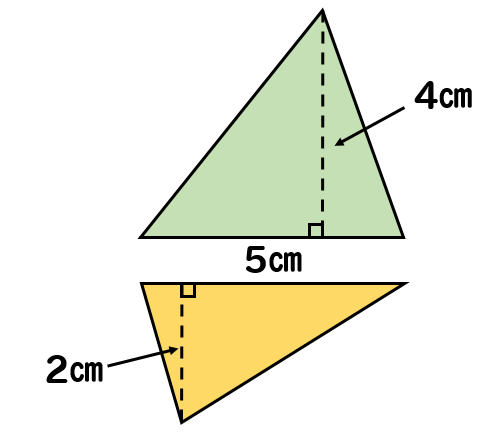
２つの三角形に分けて考えていきましょう。

上の緑三角形は底辺が5㎝、高さが4㎝だから

$$5\times 4\div2=10(cm^2)$$

 

下の黄三角形は底辺が5㎝、高さが2㎝だから

$$5\times 2\div2=5(cm^2)$$

 

以上より、四角形の面積は

$$\Large{10+5=15(cm^2)}$$

となりました。

 

面積応用問題

次はめちゃめちゃ難しい超応用問題です。

 

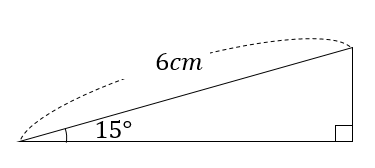
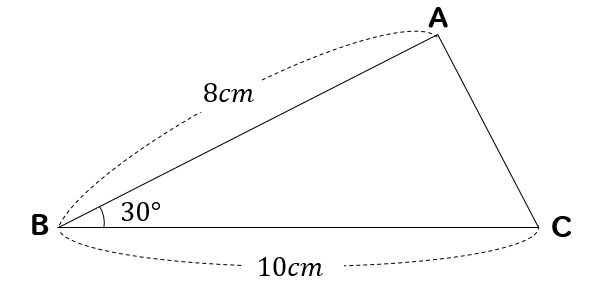
なんじゃこれは！？

高さの長さがわからんぞ…

しかも、なんか角度が与えられているし…

どうやって利用すればいいのだ…

 

この問題は中学入試レベルになります。

受験を控えている方のみ解ければOKです。

詳しい解説はこちらの記事にて。

＞【小学算数】30度の三角形ってどうやって面積求める？辺の比は？

＞【小学算数】15度、75度の三角形ってどうやって面積求めるの？

 

まとめ

お疲れ様でした(^^)

以上で三角形の面積公式はマスターだね！

三角形の面積公式は、これから算数、数学を学ぶ上で必須なモノだからしっかりと身につけておこうね。

 

ファイトだー(/・ω・)/