ひし形の面積を求める公式は
$$(対角線)\times (対角線)\div 2$$
となっています。
だけど、なぜ対角線を掛ける必要があるの？
ひし形の辺は使わないの？
って感じだよね。
そういうわけで、今回の記事ではひし形の面積公式で対角線を使う理由などについて説明してきます。
そもそも、ひし形ってなんだっけ？
ひし形っていうのは
全部の長さが等しい四角形
のことをいいます。
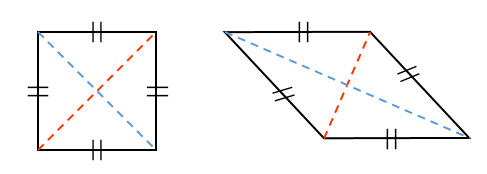
よく目にするひし形の図形っていうのは
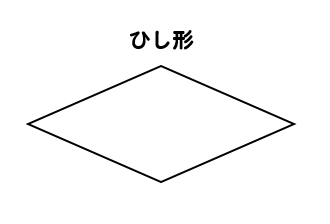
こういったのが多いと思います。
だけど、実は
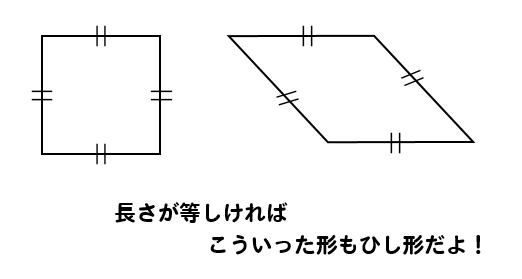
こんなのも、ひし形って言えるんだよ！
四角形の関係性としてはこんな感じ
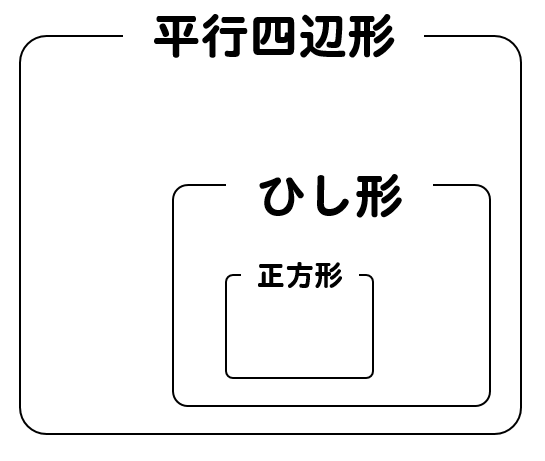
だから、正方形はひし形ってことになるね。
とにかく
長さがすべて等しい四角形はぜーんぶ、ひし形！
どれもこれもひし形の面積公式を使って
$$(対角線)\times (対角線)\div 2$$
これで計算することができるよ(^^)
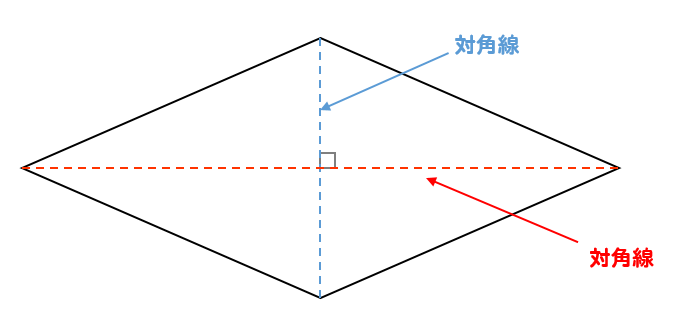
なぜ対角線をかけるの？
ひし形の面積を求めるのに、なぜ対角線を掛けるのか？
それはね
ひし形の面積を求めるために次のような図形を考えているからなんだよ！
対角線を引くと、ひし形は4つの三角形に分けられるんだけど、それらの三角形をパタンと折り返します。
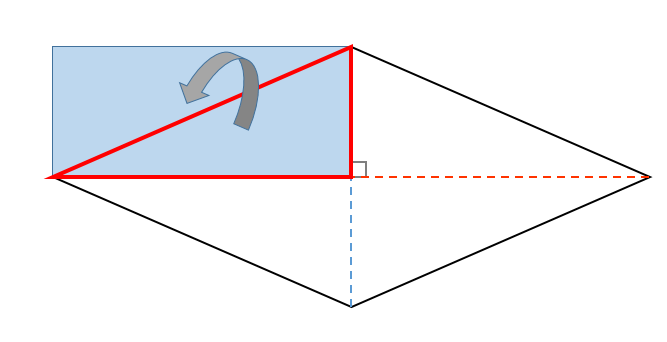
すると、こんな感じになるよね。
これをすべての三角形でやると
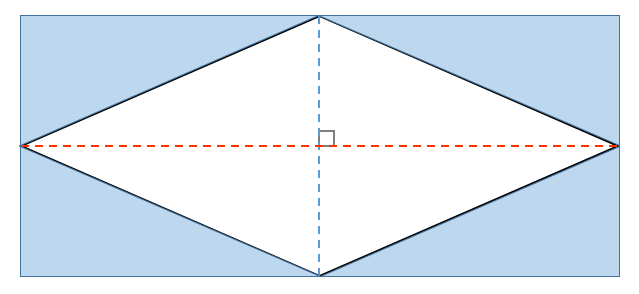
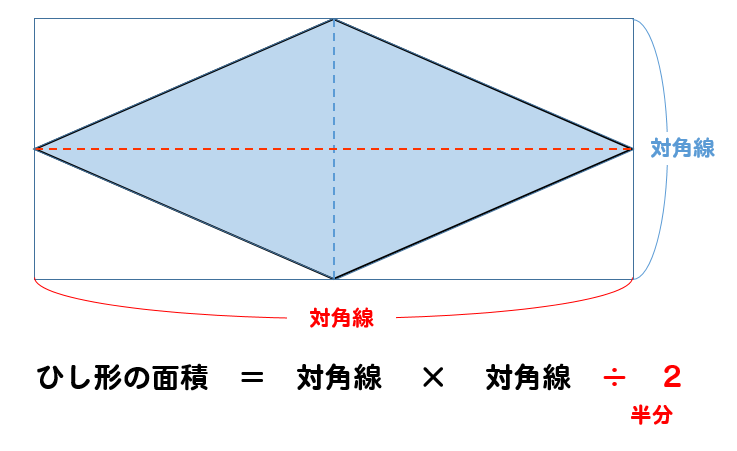
このように長方形を作ることができます。
これは、ひし形を折り返して作ったものだから面積がひし形の２倍になっています。
つまり、この長方形の面積を求め、それを半分にすることでひし形の面積を求めることができるというわけです。
この長方形のタテとヨコの長さは、ひし形の対角線と等しくなっているよね
だから、長方形の面積は
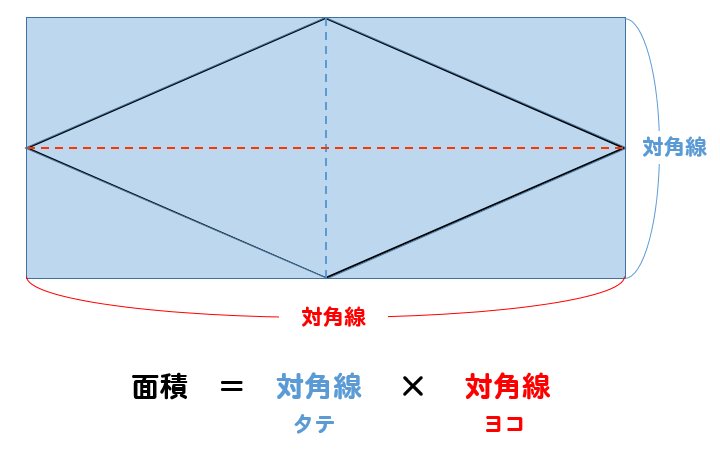
このように求めることができます。
長方形の面積が求まれば、あとは半分にするだけ！
ということで
ひし形の面積はこのように求めることができました。
つまり、ひし形の面積公式は
このように考えているのですね！
そして、ひし形の対角線にあたる部分が長方形のタテとヨコの長さになるというわけです。
ひし形の面積を求めてみよう！
それでは、ひし形の公式を使って面積を求めてみましょう。
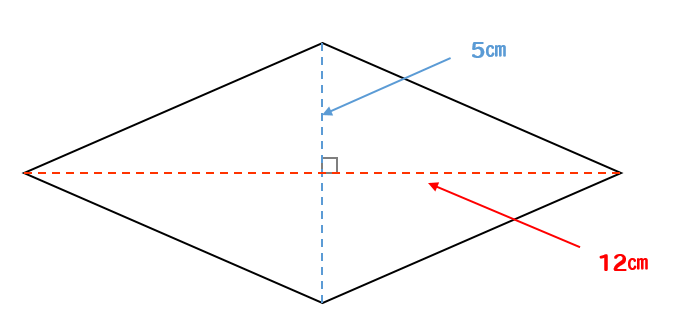
ひし形の公式に当てはめると
$$5\times 12\div 2= 30(cm^2)$$
となりました。
あら…めちゃくちゃ簡単ですね(^^;)
しっかりと意味を理解して公式を覚えておくことができれば、問題を解くのは楽勝です！
まとめ
お疲れ様でした！
多くの図形が面積を求めるのに
タテやヨコ、底辺や高さを用いるのに
ひし形だけ「対角線」を用いることから
ちょっとだけ覚えにくい公式となっています。
だけど、なぜ対角線を用いるのか？
そのことを理解してしまえば、きっと簡単に覚えることができるはずです(^^)
しっかりとひし形の面積公式を使いこなしていけるよう頑張っていきましょう(/・ω・)/
コメントを残す