今回は数学Ⅱで学習する微分積分の単元から
「極限値からの係数決定」
について学習していきましょう。
【問題】(ニューアクションβより)
\(\displaystyle \lim_{ x \to 2 } \frac{x^2+ax-b}{x-2} = 5\) のとき、定数\(a,b\) の値を求めよ。
この問題では、分子の極限値が0になることを利用して求めていきます。
ですが、なんで分子が0になるの?
という疑問を抱く人が多いと思います。
なので、その辺を詳しく解説しながら問題を解いていきますね!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
分子の極限値が0になることを利用して解く。
【問題】(ニューアクションβより)
\(\displaystyle \lim_{ x \to 2 } \frac{x^2+ax-b}{x-2} = 5\) のとき、定数\(a,b\) の値を求めよ。
まず分母の極限値を求めてみましょう。
すると…
\(\displaystyle \lim_{ x \to 2 } (x-2) = 0\)
あれ、分母が0になる…
計算ができないぞ、困ったな…
という状況になってしまいます。
ですが、分母の極限値が0になる…といったピンチを
チャンスに変えることができます!
分子の極限値を次のように考えてみましょう。
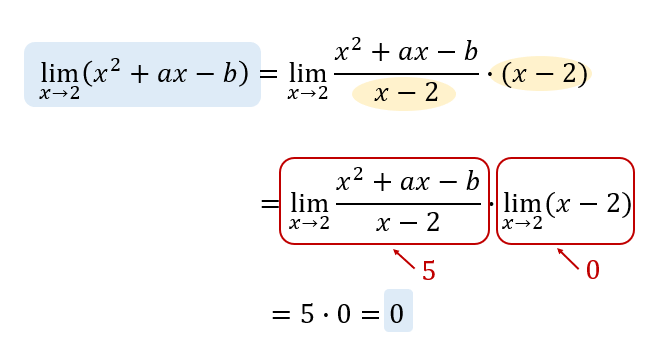
分母の極限値が0になることを利用すると、
分子の極限値も0になることが導けるのです!
\(\displaystyle \lim_{ x \to 2 } (x^2+ax-b) = 0\) になることが分かったので、
$$\begin{eqnarray}\displaystyle \lim_{ x \to 2 } (x^2+ax-b) &=& 0\\[5pt]4+2a-b&=&0\\[5pt]b&=&2a+4 \end{eqnarray}$$
という式を作ることができます。
これを元の式に代入して計算していくと、
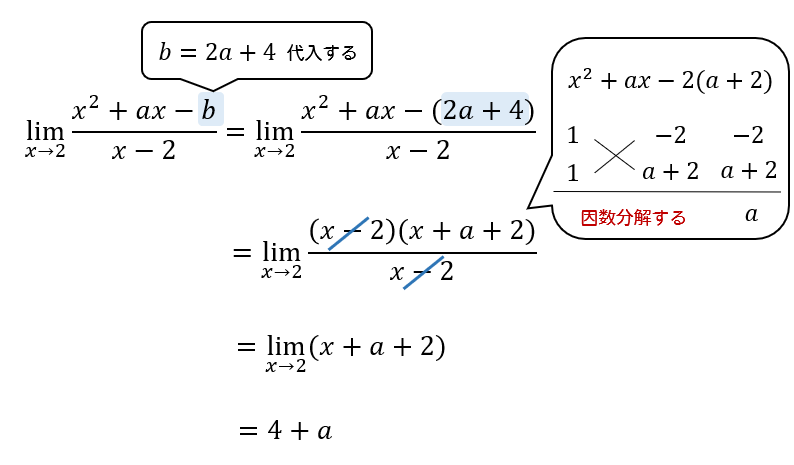
問題文より、今求めた\(4+a=5\) になるはずだから
\(a=1\) となります。
最後に、\(a=1\) を\(b=2a+4\) に代入すると
\(b=2+4=6\) となります。
答え
$$a=1,b=6$$
今回の問題でのポイントは、
\(\displaystyle \lim_{ x \to a } \frac{f(x)}{g(x)} = k(定数)\) において、
分母の極限値が0( \(\displaystyle \lim_{ x \to a }g(x) = 0\) )になる場合
⇒ 分子の極限値も0( \(\displaystyle \lim_{ x \to a }f(x) = 0\) )になる!
という点ですね。
その理由については、上の式変形をしっかりと覚えておいてくださいね(^^)
では、類似問題を解いて理解を深めておきましょう!
練習問題に挑戦!
【問題】(ニューアクションβより)
\(\displaystyle \lim_{ x \to 1 } \frac{x^2+ax+b}{x^2-1} = 2\) のとき、定数\(a,b\) の値を求めよ。
まとめ!
お疲れ様でした!
今回の問題では、分子の極限値が0になることを利用する。
これが最大のポイントでしたね。
なぜ分母の極限値が0になると、分子の極限値も0になるのか。
これについては、
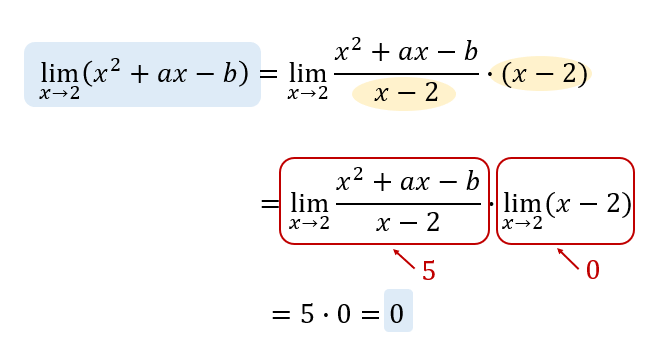
こちらの式変形を理解しておけば大丈夫ですね!



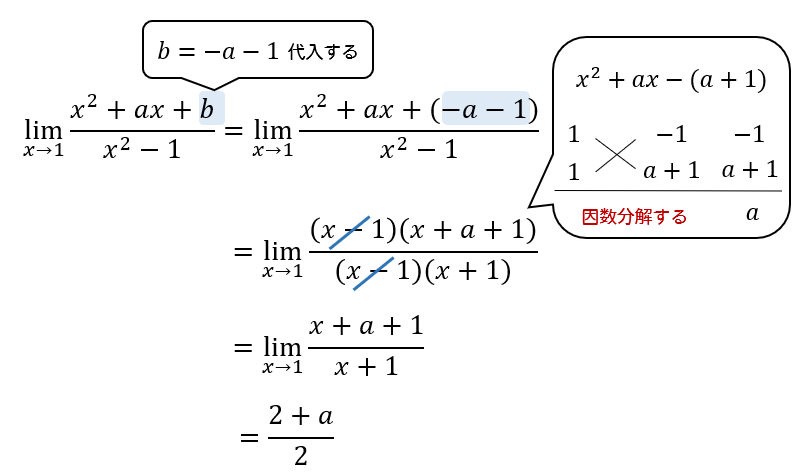












参考になったンゴ
理屈がが分からず、とても馬鹿にされたのですが、このやり方を知りよく理解できました。ありがとうございます。
とてもよく理解できました!ありがとうございます。