【旅人算】問題の解説まとめ！それぞれのパターンの解き方は？

今回の記事では、「旅人算」とよばれる問題の解き方、考え方についてまとめていきます。

旅人算とは、速さの違う二人が、出会ったり追いついたりするときの時間や道のりを求める問題のことです。

中学生になると、方程式というくくりで学習するようになるのですが小学算数では旅人算という考え方を使って解いていきます。

それでは、旅人算とは一体どのような解き方、考え方なのでしょうか。

【旅人算】問題の解説まとめ！

旅人算では、実に様々なパターンの問題が出題されます。

それでは、それぞれのパターンについて解き方を確認していきましょう。

【旅人算】出会うパターンの解き方

2人が出会うというのは…

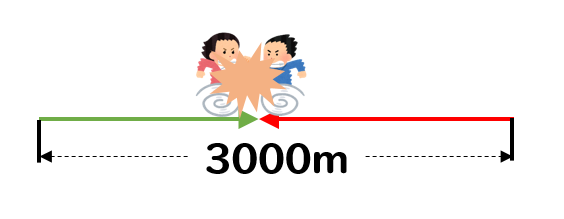
2人が進んできた道のりの和が3000mになるということです。

この考え方がとっても大切！

2人が出発して、1分後の状況を考えてみましょう。

すると、このように二人はそれぞれ70m、80m進んでいることが分かります。

つまり、2人は1分で合計150m進んだことになります。

2人の進んだ道のりが合計3000mになれば、2人は出会うのだから

$$3000\div150=20分$$

このようにして、2人が出会うまでの時間を求めることができます。

【旅人算】追いつくパターンの解き方

まずはAさんが先に出発し、8分間進んでいるので \(60\times 8=480m\)

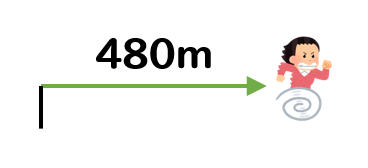
このような状況になっています。

そこからBくんが出発すると、速さの差から2人の道のりの差は1分で40mずつ縮まることが分かります。

そして、この差が0になったときが追いついたときということになります。

よって、480mあった二人の差が1分間で40mずつ縮まっていくということを考えると

$$480\div 40=12分後$$

このようにして、2人で出会うまでの時間を求めることができます。

【旅人算】池の周りをまわるパターンの解き方

まず、2人が反対方向に進む場合

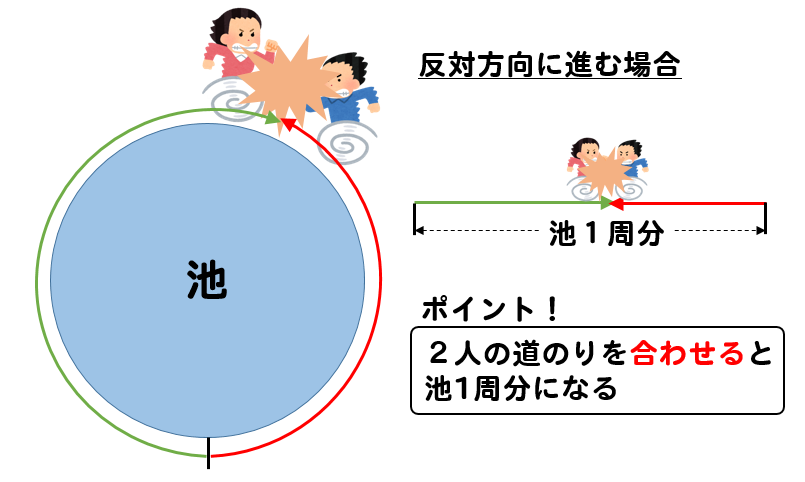
上で紹介した2人が出会うパターンと同様に考えればOKです。

2人が進んだ道のりの和が池1周分の道のりになったとき、2人は出会うことになります。

1分後の状況を考えると、Aくんは120m、Bさんは180m進むので、2人合わせて300m進んだということになります。

よって、池1周分の距離は2400mであることから

$$2400div 300=8分後$$

このようにして、池の周りを反対に進むときに出会うまでの時間を求めることができます。

次に、2人が同じ方向に進む場合

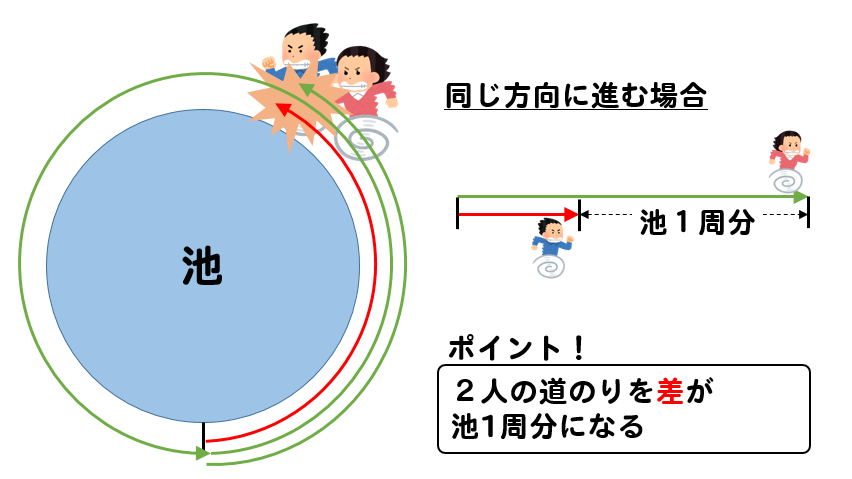
上で紹介した2人が追いつくときのように、差を考えながら解いていきます。

2人の進んだ道のりの差が池1周分である2400mになれば、追いついたことになります。

2人の速さの差を考えると、1分間に\(180-120=60m\) だけ差が広がっていくことになるので

$$2400\div60=40分後$$

このようにして、池の周りを同じ方向にに進むときに追いつくまでの時間を求めることができます。

【旅人算】往復を考えるパターンの解き方

往復を考える場合

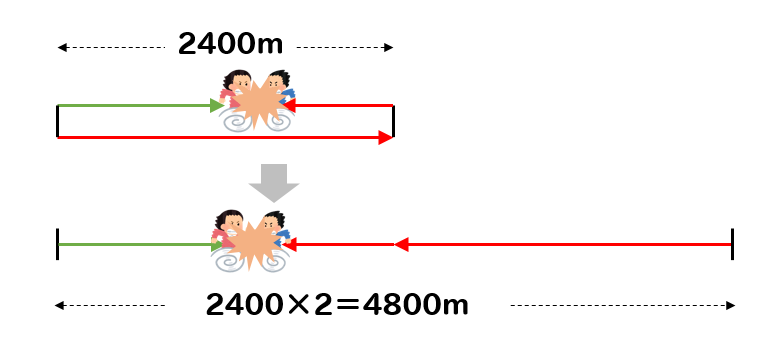
こんなイメージ図になりますね。

つまり、2人の進んだ道のりの合計が、家から駅までの往復の距離と等しくなったときに出会うということです。

1分間で、2人はそれぞれ50m、70mずつ進むので合計で120mずつ進むことが分かります。

よって

$$4800\div 120=40分後$$

このようにして、往復する場合に追いつくまでの時間を求めることができます。

旅人算の問題まとめ！

お疲れ様でした！

旅人算には、いろいろなパターンの出題がありますが、どれにおいても2人の速さの合計や差を考えていくこととなります。

合計か差か…

どちらを利用すれば良いのかについては、イメージ図を書いて考えてみるといいですね。

出会うから合計で…追いつくから差で…

というように言葉で暗記してしまうと、応用問題が出題されたときに困ってしまいます。

そうならないためにも頭の中でイメージをしっかりと持っておくことが大事ですね(^^)