【時計算の問題解き方は？】角度の公式を覚えるべし！！

今回は「時計算」という問題の解き方、考え方について解説していきます。

時計算とは、時計の長針と短針がそれぞれどれくらい動き、そしてどのような角度をなすのか。

ということについて考えていく問題です。

3時30分のとき、長針と短針の間って何度？？

こんなこと日常生活の中で考えたこともないよね(^^;)

なので、どうやっていいか分かんねぇ…

と、なってしまうのですが

そこは、この記事を通してポイントを押さえてもらえれば簡単に解けるようになりますよ★

ってことで時計算、マスターしていきましょう！

時計算の覚えておきたい公式

公式っていうほどのことではありませんが、時計算を解いていく上で覚えておきたいことがことがあります。

長針は1時間（60分）で1周、つまり360°回転します。

ってことは、\(360\div60=6\) となり、1分では6°動くということがわかります。

一方で、短針の方は12時間（720分）で1周、つまり360°回転します。

なので、\(360\div 720=0.5\) となり、1分で0.5°動くということがわかります。

1分間にそれぞれ6°と0.5°ずつ動いていくので、長針と短針は毎分5.5°ずつ差が変化していくってこともわかるね！

では、これらのことを頭に入れた上で時計算の問題を見ていきましょう。

【時計算の解き方】〇時〇分の角度

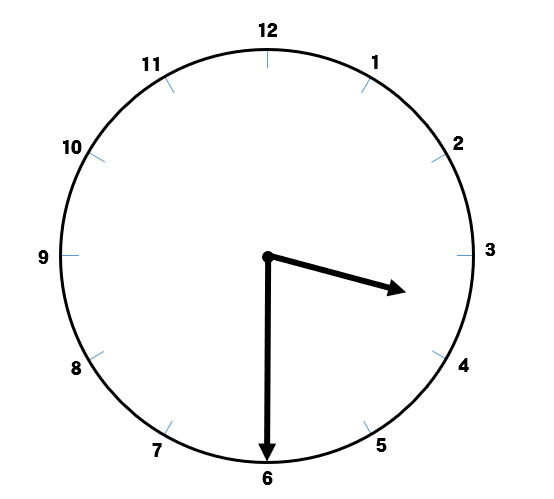
まずは、キリのよい3時00分の状態から考えていきます。

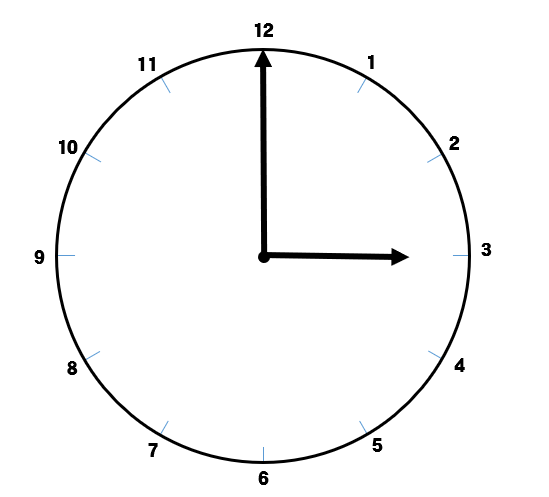
すると、ここから30分の間に長針は

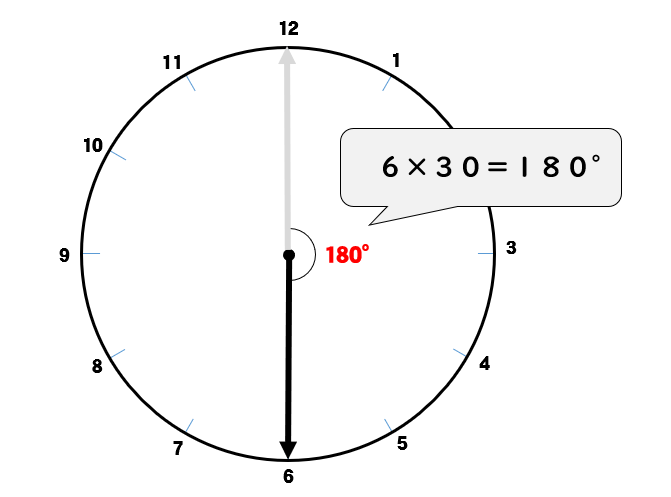
\(6\times 30=180°\) 動いています。

短針のほうは、初めに90°の位置にあり

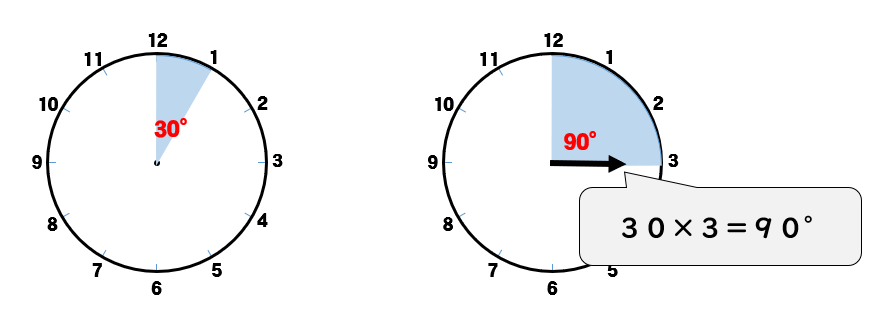
そこから30分の間に

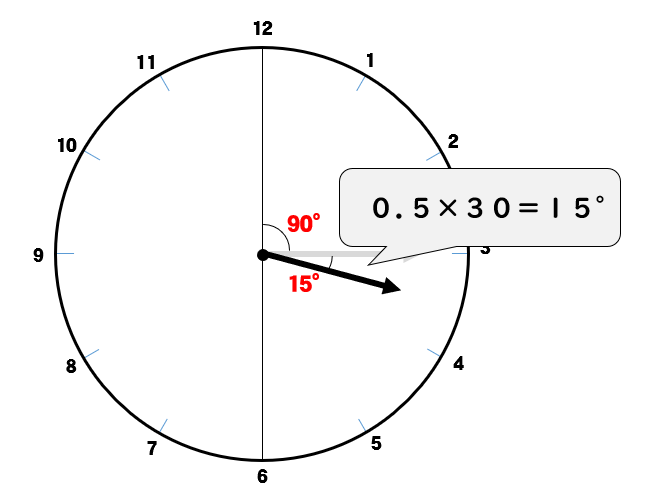
\(0.5\times 30=15°\) 動いています。

ということは、3時30分での位置は \(90+15=105°\) ってことになりますね。

以上より

長針と短針のつくる小さいほうの角度は

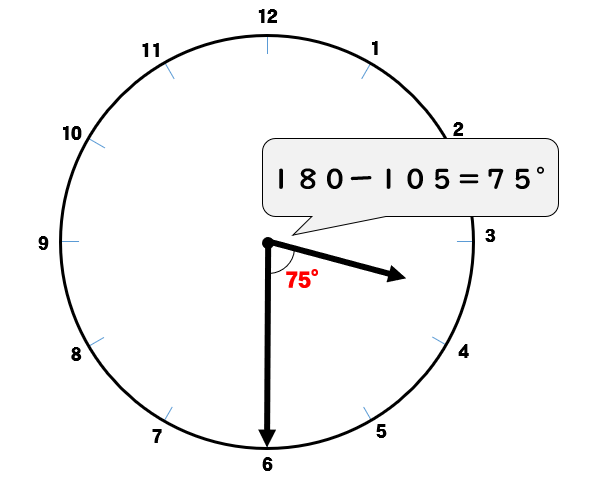
$$180-105=\color{red}{75°}$$

ということが求まりました！

ある時間での長針と短針のつくる角度を求める場合

まずは、キリの良い〇時00分の状態を考えましょう。

そこから長針がどれくらい動いたのか。

短針の初めの位置

そして、そこからどれくらい動いたのか。

これらを求めることで、角度を求めることができます。

では、やり方を身につけるためにいくつか練習問題に挑戦してみてください。

練習問題に挑戦！

【時計算の解き方】ぴったり重なるのは何分？？

重なるという問題では、1分間でできる長針と短針の角度の差に注目します。

1分で動く長針と短針の角度の差は5.5°

これを頭に入れて問題を解いていきましょう！

3時00分のとき

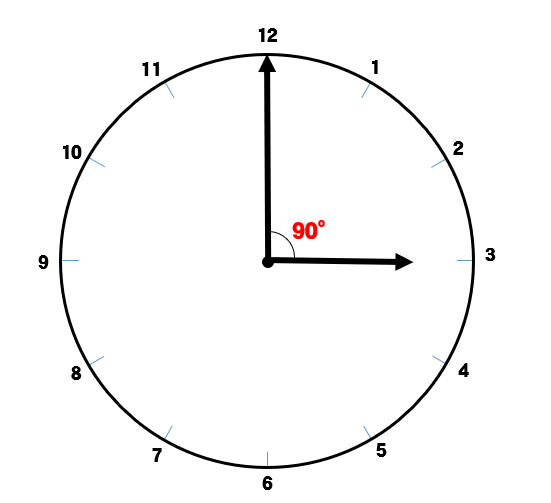
長針と短針の間には90°の差があります。

この差が0°になったとき、長針と短針はぴったり重なるってことになります。

1分で長針と短針は5.5°ずつ近づいていくので

$$\begin{eqnarray}90\div 5.5&=&90\div \frac{55}{10}\\[5pt]&=&90\times \frac{2}{11}\\[5pt]&=&16\frac{4}{11} \end{eqnarray}$$

よって、3時から4時の間でぴったり重なる時刻は

$$3時16\frac{4}{11}分$$

となります。

重なるという問題では、1分間で5.5°の差が縮まるということを覚えておけば簡単ですね(^^)

練習問題

【時計算の解き方】針のつくる角度が〇°になるのは何分？？

長針と短針のつくる角度が60°になるには、次の2パターン考えられます。

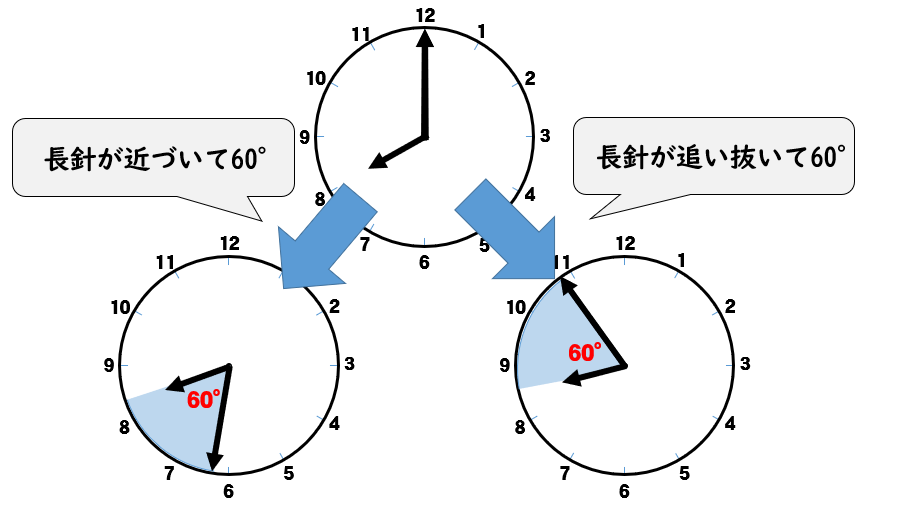
まずは、長針が短針に近づいて60°になるパターンから求めます。

8時00分の時点で、長針と短針の角度は240°あります。

この角度が180°縮まれば、角の大きさは60°になります。

よって、\(180\div5.5=32\frac{8}{11}\)分。

次は、追い抜いて60°パターンを考えます。

こちらは長針が短針に追いき、そこから60°の差を作ったってことだよね

つまりは、\(240+60=300°\)分だけ長針と短針の動きに差ができたってこと！

よって、\(300\div5.5=54\frac{6}{11}\)分。

以上より、答えは

$$8時32\frac{8}{11}分　と　8時54\frac{6}{11}分$$

となります。

〇°になるとき

というのは、長針と短針のはじめの角度に対し

$$\{(初めの角度)-(作りたい角度)\}\div 5.5$$

$$\{(初めの角度)+(作りたい角度)\}\div 5.5$$

これを考えれば、すぐに求めることができますね(^^)

練習問題

時計算まとめ！

以上！時計算の問題についてでした。

どの問題においても、初めて挑戦する場合にはすっごく難しく感じちゃいますよね(^^;)

だけど、長針と短針の動きについて理解ができていれば大丈夫！

これをしっかりと頭に入れておきましょうね(^^)