【算数】分数と小数の混じった計算方法とは？解き方を１から解説！

分数、小数…

$$\LARGE{\frac{1}{3}+0.2}$$

あれ、見た目が全然違うけど、どうやって計算するんだっけ？

小学生のお子さんに質問されて、困ってしまった経験はありませんか？(^^;

こんな計算、日常生活で使わないもんねｗ

大人になっちゃうと忘れてしまうのも分かります。

だけど、お子さんにはデカい顔して、ちゃんと教えてあげたいですよね。

というわけで！

今回は、分数と小数の混じった計算問題の解き方について学んでいきましょう！

分数、小数の形を揃えよう！

分数、小数が混じってる計算問題では、形を揃えてから計算をしていきます。

分数、小数の形のままだと計算が困難です。

あなたが手元に10ドルと10円のお金を持っているとします。

さて、あなたの手元には合計でいくらありますか？？

え、えーーーっと…

お金の単位が違うから、わからん！！

ってなっちゃうよね。

でも、ドルを円に換金してやれば、簡単に合計を求めることができるはずです。

1ドルを100円として考えさせてもらうと

10ドル＝1000円だから

1000円＋10円＝1010円ということになります。

分数と小数の計算もこういうイメージを持ってみてください。

形が違うモノどうしだと計算が難しいですよね。

というわけで

分数に揃える

$$\LARGE{\frac{1}{3}+0.2}$$

$$\LARGE{=\frac{1}{3}+\frac{1}{5}}$$

小数に揃える…？

$$\LARGE{\frac{1}{3}+0.2}$$

$$\LARGE{=0.333\ldots+0.2}$$

小数に揃えようとした場合、このように表せなくて困ってしまうケースもあるので分数に揃える方が良いですよ(^^)

小数を分数に変換する方法をサクッとやっちゃいましたが

ここも苦手な人が多いところです。

忘れちゃったなーという方は、次のところで確認していきましょう。

小数を分数に変換する方法

それでは、小数を分数に変換する方法を確認しておきましょう！

とっても簡単なことですよ(^^)

考え方としてはこんな感じです。

$$\Large{0.3=3\div 10=\frac{3}{10}}$$

0.3というのは3から小数点を左に1つ動かした数ですね。

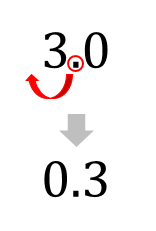
つまり、3を10で割った数ということ。

そして、わり算を分数の形で表したモノが\(\displaystyle \frac{3}{10}\)というわけです。

なんで\(\displaystyle \frac{3}{10}\)になるのか？？

分数の割り算を思い出してみましょう。

$$\Large{3\div 10=3\div \frac{10}{1}}$$

$$\Large{=3\times \frac{1}{10}}$$

$$\Large{=\frac{3}{10}}$$

こういう感じで考えてもらえればOKかな？

それでは、いろんな小数を分数に変換してみましょう。

$$\Large{0.02=2\div 100=\frac{2}{100}=\frac{1}{50}}$$

最後に約分も忘れないようにね！

$$\Large{1.41=141\div 100=\frac{141}{100}}$$

$$\Large{0.0003=3\div 10000=\frac{3}{10000}}$$

こんな感じで小数を分数に変換することができます。

至ってシンプルな考え方ですよね！

小学生の内は、小数点に注目して

という感じで変換できれば大丈夫かな(^^)

分数を小数に変換する方法

今回の計算では活用しませんが、分数を小数に変換する方法についても触れておきますね。

これは、先ほどの変換を逆に辿ればOKです。

$$\Large{\frac{3}{10}=3\div 10=0.3}$$

こんな感じです。

（分子）÷（分母）

この形を覚えておけば大丈夫です！

$$\Large{\frac{141}{100}=141\div 100=1.41}$$

$$\Large{\frac{3}{10000}=3\div 10000=0.0003}$$

それでは、形を揃える方法を学んだところで実践に入っていきましょう。

分数・小数の足し算・引き算

まず、小数を分数に変換して形を揃えてあげましょう。

$$\LARGE{\frac{1}{4}+1.2}$$

$$\LARGE{=\frac{1}{4}+\frac{6}{5}}$$

分数の形に揃えることができたので、ここから通分をして計算していきましょう。

$$\LARGE{=\frac{5}{20}+\frac{24}{20}}$$

$$\LARGE{=\frac{29}{20}}$$

完成！

簡単でしたね(^^)

それでは、理解を深めるために演習問題にも挑戦してみましょう。

分数・小数のかけ算・割り算

かけ算、わり算においても手順は同じです。

まずは分数に形を揃える！ですね

$$\LARGE{\frac{3}{5}\times 1.5}$$

$$\LARGE{=\frac{3}{5}\times \frac{3}{2}}$$

かけ算、わり算では通分は必要ありませんので、そのまま計算していきます。

$$\LARGE{=\frac{3\times 3}{5\times 2}}$$

$$\LARGE{=\frac{9}{10}}$$

それでは、こちらも演習問題を通して理解を深めていきましょう！

まとめ

お疲れ様でした！

たくさんのことを頭に詰め込んだので疲れましたねｗ

それでも、やってみると簡単なことだなって分かってもらえたと思います。

見た目は難しそうな問題でも、やり方を順に学べば必ずできるようになります。

この調子で、どんどんといろんな問題にも緒戦してもらいたいです(^^)

分数の通分、苦手な人多いよね…

そんなときに使えるちょっとしたテクニック！

【算数】分数を通分するときの最小公倍数を簡単に見つける方法を解説！

ぜひ、こらもご参考ください＾＾