この記事では、小学生で学習する知識だけを利用して
15度の三角形の面積を求める方法について解説していきます。
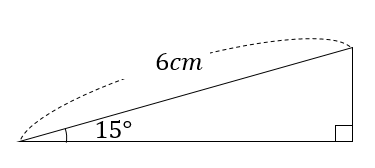
この問題を解くためには、30度三角形の特徴を知っておく必要があります。
30度の特徴？なんじゃそりゃっていう人は
まず、こちらの記事をお読みください。
15度の直角三角形には必ず75度も含まれることになります。
ですので、15度の三角形の面積について理解できれば、
同時に75度の三角形もクリアすることができるようになります！
というわけで、今回の記事では
15度の三角形について取り上げ、解説していきますね(/・ω・)/
15度三角形の面積の求め方
それでは、15度三角形の面積を求める手順を紹介していきます。
15度の三角形は、30度に変換して考える
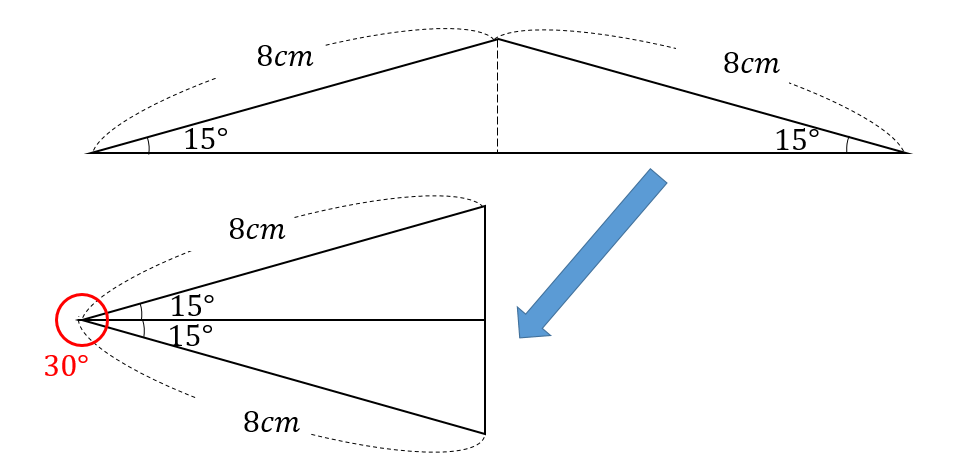
15度の三角形の面積を考える場合には
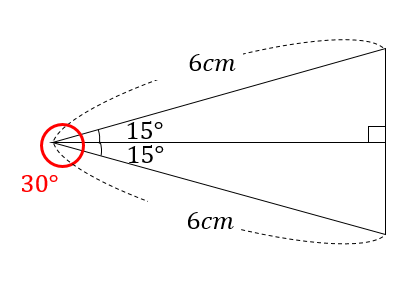
このように、15度三角形を2つ分にして
角が30度になるように三角形を作ってやります。
15度三角形のままだと、面積を求めるのがどうしても難しいので
30度の三角形の面積を求めて
それを半分にすることで、15度三角形の面積を求めていきます。
30度三角形の特徴を利用して、高さを求める
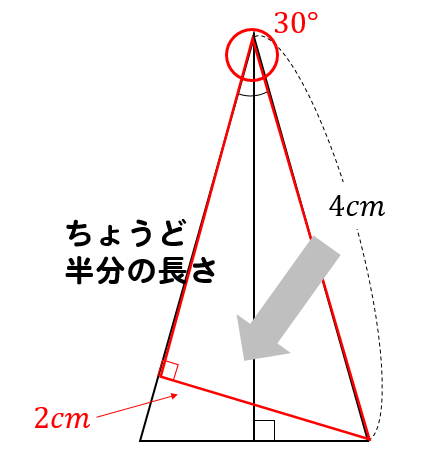
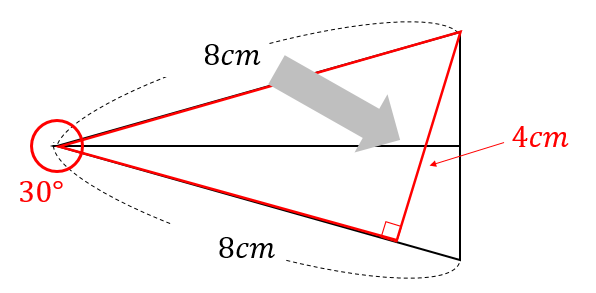
ここから、30度三角形の辺の長さの特徴を利用して
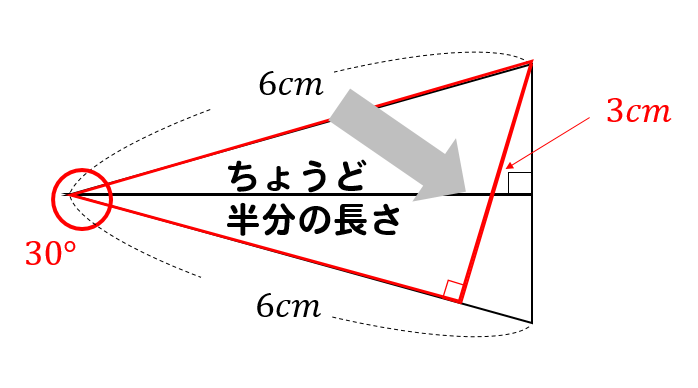
このように、高さとなる部分の長さを求めてやります。
高さが求まったら面積を求める
高さがわかったら、30度三角形の面積を求めます。
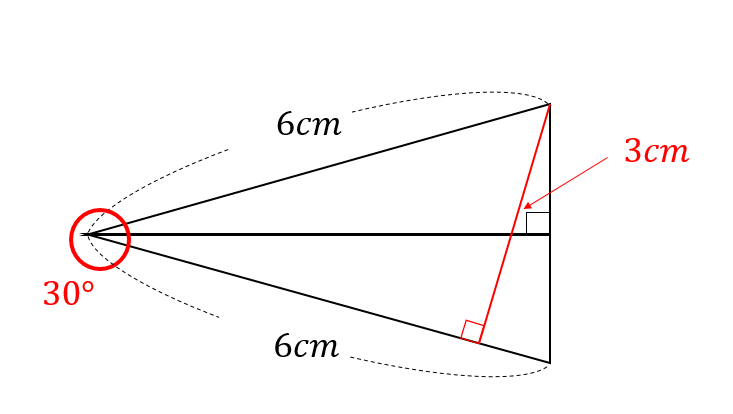
底辺6㎝、高さ3㎝ということが読み取れるので、面積は
$$\LARGE{6\times 3\times \frac{1}{2}}$$
$$\LARGE{=9(cm^2)}$$
そして、15度三角形の面積は
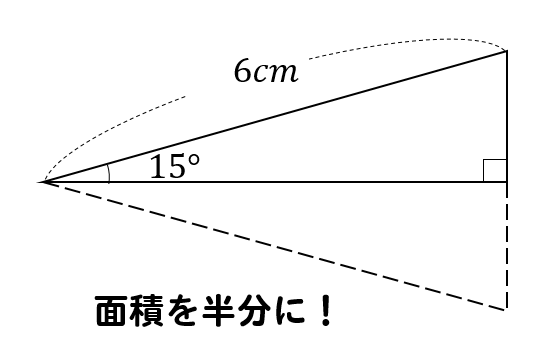
先ほど求めた面積を半分にして
$$\LARGE{9\div 2=4.5(cm^2)}$$
となります。
15度三角形の面積公式とは
それでは、上で紹介した解き方の手順を
公式っぽくまとめておきますね！
上の手順を1つの式にまとめるとこのようになります。
もう少し、計算を進めていくと
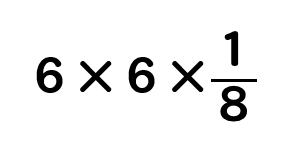
このように表すことができます。
これより、公式っぽくまとめておくと
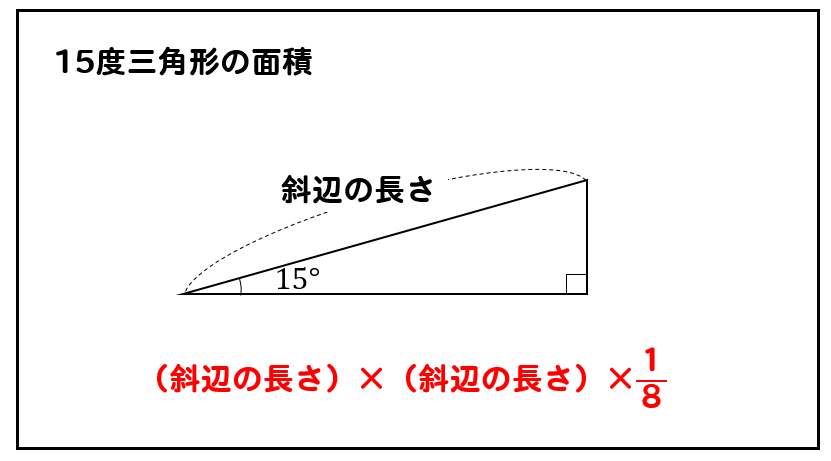
覚えておくと、ちょっと得するかもしれませんね！
それでは、理解を深めるために練習問題に挑戦してみましょう。
練習問題に挑戦！
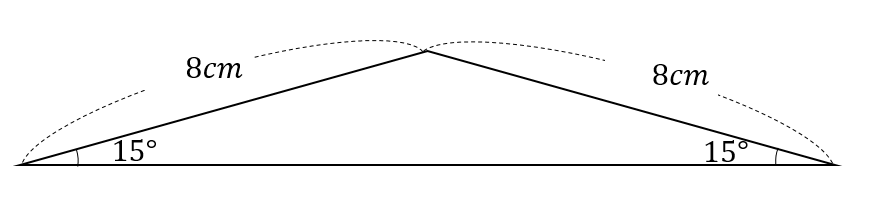
次の三角形の面積を求めなさい。
答え
$$2(cm^2)$$
このように高さを求めることができるので
30度三角形の面積は
$$4\times 2\times \frac{1}{2}=4$$
よって、15度三角形の面積は
$$4\div2=2$$
となります。
公式を利用すると
$$4\times 4\times \frac{1}{8}=2$$
このように簡単に求めることもできます。
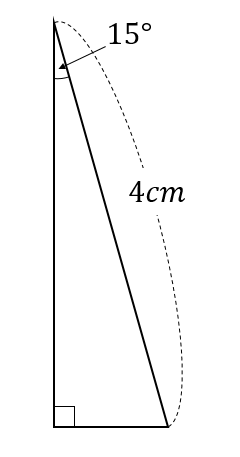
次の三角形の面積を求めなさい。
答え
$$16(cm^2)$$
二等辺三角形を半分に割って、くっつけることで30度の角を持つ三角形に変形してやりましょう。
この形が作れれば、今までと考え方は一緒ですね。
30度三角形の特徴を利用して、高さを求めると4㎝となります。
よって、面積は
$$8\times 4\times \frac{1}{2}=16(cm^2)$$
となります。
まとめ
お疲れ様でした！
15度三角形の面積は、30度の角を作ることで求めることができましたね。
面積を求める手順をしっかりと覚えておきましょう！
手順をマスターできた人は、公式を利用して
ちょっと楽に計算してもOKです！
たくさん練習して、しっかりと身につけておきましょう。
ファイトだー(/・ω・)/
タイトルは15度と75度の三角形の面積の求め方なのですが、本文は15度だけで、75度の三角形の面積の求め方が書いてない、気がします。15度と同じ、という一文言及だけで十分なのですが。（読み落としだったら失礼しました）
たしかに、タイトルと記事内容の解説にズレがあるように感じます(^^;)
アドバイスいただいた通り、
記事の冒頭で75度についても触れることにしました。
ご指摘ありがとうございました！
なるほど