今回は『正負の数の利用』である平均を使った問題について解説していきます。
平均を使った問題とは
下の表は、ある図書館の先週の貸し出し冊数を100冊を基準にして、それより多い場合を正の数、少ない場合を負の数で表したものである。次の問いに答えなさい。
| 曜日 | 月 | 火 | 水 | 木 | 金 |
| 基準との差 | +3 | -2 | +12 | -7 | +9 |
(1)木曜日の貸し出し冊数は何冊か。
(2)水曜日の貸し出し冊数は木曜日より何冊多いか。
(3)先週の貸し出し冊数の平均を求めなさい。
こんな感じのやつだね!
文章問題ということもあって、苦手意識を持っている人も多いようですが、そんなに難しい問題ではないからサクッと理解してしまいましょう(^^)

(1)の解説 基準との差を考える
下の表は、ある図書館の先週の貸し出し冊数を100冊を基準にして、それより多い場合を正の数、少ない場合を負の数で表したものである。次の問いに答えなさい。
| 曜日 | 月 | 火 | 水 | 木 | 金 |
| 基準との差 | +3 | -2 | +12 | -7 | +9 |
(1)木曜日の貸し出し冊数は何冊か。
木曜日は、-7ということから基準である100冊よりも7冊少ないということが分かります。
$$100-7=93冊$$
簡単ですね!
問題文から基準となる冊数を読みっていれば楽勝です。
他の曜日についても冊数を求めると
【月】\(100+3=103(冊)\)
【火】\(100-2=98(冊)\)
【水】\(100+12=112(冊)\)
【木】\(100-7=93(冊)\)
【金】\(100+9=109(冊)\)
このようになることが分かります。
(1)答え
$$93(冊)$$
(2)の解説 基準との差を考える
下の表は、ある図書館の先週の貸し出し冊数を100冊を基準にして、それより多い場合を正の数、少ない場合を負の数で表したものである。次の問いに答えなさい。
| 曜日 | 月 | 火 | 水 | 木 | 金 |
| 基準との差 | +3 | -2 | +12 | -7 | +9 |
(2)水曜日の貸し出し冊数は木曜日より何冊多いか。
水曜日は基準よりも12冊多く、木曜日は基準よりも7冊少ないことが分かります。
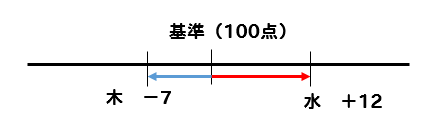
よって、どれくらいの差があるかといえば
$$+12-(-7)=12+7=19(冊)$$
ということが分かります。
差が大きい方から、差が小さい方を引いてやることで互いがどれだけ離れているかを求めることができます。
他にも、(1)でやったように基準の値から具体的な冊数を求めてから考えるというのもアリです。
水曜日は112冊、木曜日は93冊でしたから
$$112-93=19(冊)$$
とやってしまってもOKです。
だけど、差の数を使って計算した方が楽なのは間違いないですね(^^;)
(2)答え
$$19(冊)$$
(3)の解説 基準との差を考える
下の表は、ある図書館の先週の貸し出し冊数を100冊を基準にして、それより多い場合を正の数、少ない場合を負の数で表したものである。次の問いに答えなさい。
| 曜日 | 月 | 火 | 水 | 木 | 金 |
| 基準との差 | +3 | -2 | +12 | -7 | +9 |
(3)先週の貸し出し冊数の平均を求めなさい。
ちょっと応用的な平均の求め方になりますが
このように考えていきましょう。
というわけで、先週5日間の基準との差の平均を求めます。
$$\frac{(+3)+(-2)+(+12)+(-7)+(+9)}{5}=\frac{15}{5}=3(点)$$
つまり、先週は毎日、基準よりも平均+3冊借りられていたことが分かりました。
よって、先週の貸し出し冊数の平均は
$$100+3=103(冊)$$
となりました。
または、ちょっとシンドイですが計算を頑張って平均を求めるという方法もあります。
基準との差を考えるのではなく、それぞれの曜日の冊数を求めてから平均を求めるという方法です。
この場合には
$$\frac{103+98+112+93+109}{5}=\frac{515}{5}=103(点)$$
このように計算することができます。
大きい数字を使って計算していくことになるので、ミスが起こりやすくなってしまいます…
なので、なるべく上で紹介したような基準との差を考えながら平均を求める方がおススメですね。
(3)答え
$$103(冊)$$

正負の数利用の練習問題!
下の表は、5人の生徒のテスト結果を表にまとめたものです。80点を基準として、それより多い場合を正の数、少ない場合を負の数で表したものである。次の問いに答えなさい。
| 生徒 | A | B | C | D | E |
| 基準との差 | +7 | +12 | -3 | -1 | +5 |
(1)Bのテストは何点か。
(2)5人のうちで、もっとも高い点数と最も低い点数の差は何点か。
(3)5人の点数の平均を求めなさい。
【特典】最後まで取り組んでくれた方への追加教材!
お疲れ様でした^^
練習問題もしっかり解けましたか??
今回の問題が解けるようになれば応用はバッチリ、入試問題だって解けるようになりますよ^^
というわけで、最後まで取り組んでくれたお礼として、入試問題からピックアップした追加演習を用意したのでチャレンジしてみましょう!
- 正負の利用問題のポイント&演習をまとめたプリント

今回の課題をお子さんと一緒に取り組んでいただくことで、次のようなメリットがあります!
お休みの日などを利用して、ぜひ家庭学習にご活用ください^^
- 応用力が高まり、80、90点以上を狙っていく土台ができあがる!
- 学校の授業だけではカバーしきれない発展問題がラクラク解けるようになる!
- やり終えたプリントをノートに貼っておけば、いつでも簡単に復習ができるのでテストまで記憶がバッチリ定着!
- 10分で取り組めるので、習い事の合間などスキマ時間を使って勉強できる
- 参考書を買ったり、塾に行かなくても正負の加減はこれだけでバッチリ仕上がる!
それでは、今回の利用問題が入試ではどのように出題されるのかチェックしておきましょう!
これが解けたら正負の数はクリアかもしれませんね^^
というわけで、今すぐチャレンジしてみよう!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます。
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定です。
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
正負の数利用(平均)まとめ!
お疲れ様でした!
文章が長かったり、表が複雑に見えたりしてパッと見では難しそうな問題なのですが、実際に解いてみれば楽勝でしたね(^^)
最後の平均を求めるところだけ、ちょっと工夫が必要でした。
基準値が与えられた場合には、基準値との差を利用して平均を求めていくようにしましょう。
以上だ(/・ω・)/
- 正負の数とは?
- 絶対値とは?
- 大小関係を不等号で表すためのポイント
- 加法・減法をマスターしよう!
- 乗法・除法をマスターしよう!
- 累乗の計算とは
- 正負の数、分数計算のやり方を問題解説!
- 正負の数の利用、平均を使った問題を解説! ←今回の記事
- 正負の数の問題まとめ!計算のやり方を確認しよう!
★上級者向け★


















この問題を解いてとても理解することができた。このサイトを見て、テストでも良い点数をとることができた。
良い点が取れたということで、
おめでとうございます!
とても嬉しい報告ありがとうございました(^^)
最高?