【植木算が苦手？】考え方と解き方を問題解説！

小学算数で学習する『植木算』ですが

イメージが掴みにくくて苦手…という方も多いようです。

今回の記事では、図を使いながら

植木算３つのパターンについて考え方と解き方を解説していきます。

植木算3パターンと考え方・解き方

植木算には以下3パターンの出題があります。

どのように考えて、解いていけば良いのか見ていきましょう。

両端も木を植えるパターンの考え方・解き方

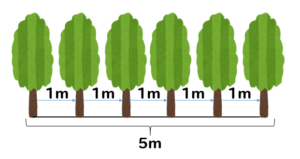
イメージとしては、こんな感じですね。

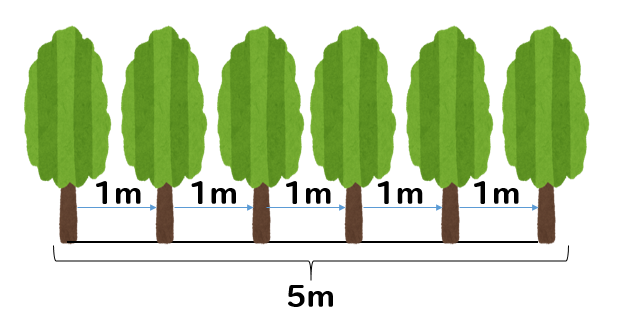
図を見れば、すぐに木が6本必要だということがわかります。

だけど、あれ…

5mの道なのに、なんで6本なの？

ちょっと分かんない…

となってしまいます。

そういう方は、０のイメージを持っておきましょう。

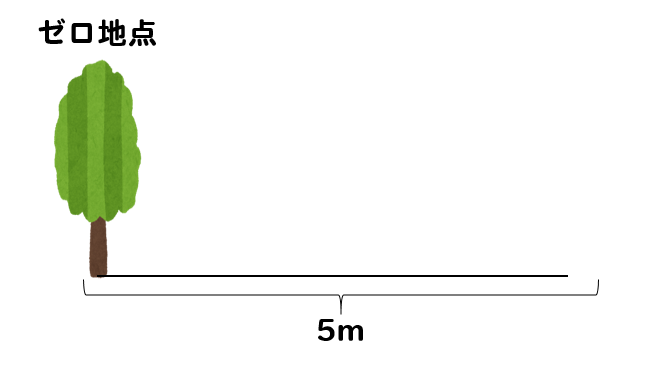
スタート地点に木を植えるので、そこが０地点！

そこから1mという間隔がいくつできる考えれば木の本数が分かってくるはずです。

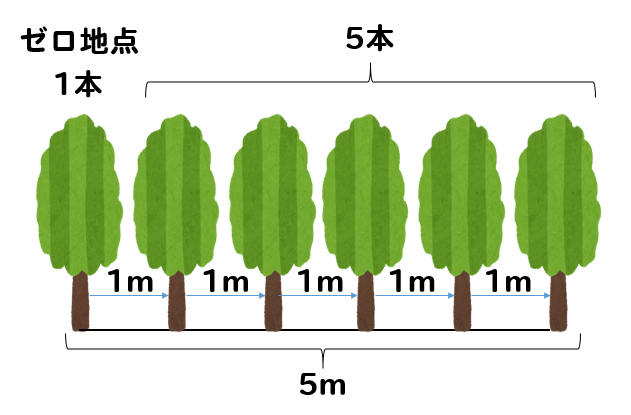
この考え方を公式っぽく表したモノがこれです。

それでは、練習問題に挑戦してみましょう。

両端は木を植えないパターンの考え方・解き方

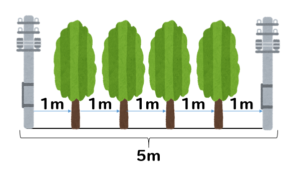
両端には電柱が立っているので、イメージとしてはこんな感じ。

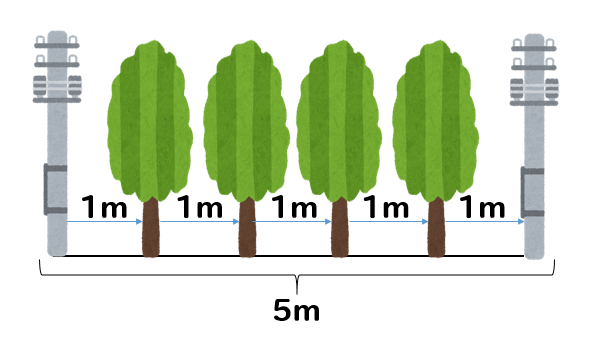
間が５つできるのに対し、木の本数は4本であることが分かります。

公式っぽくしたものがコレです。

もしくは、両端に木を植えた場合の木の本数を求めて、そこから両端にある2本分を引くという考え方を使って解いてもOKです。

それでは、練習問題に挑戦してみましょう。

池のまわりに木を植えるパターンの考え方・解き方

池のまわりに木を植えると、次のようなイメージになります。

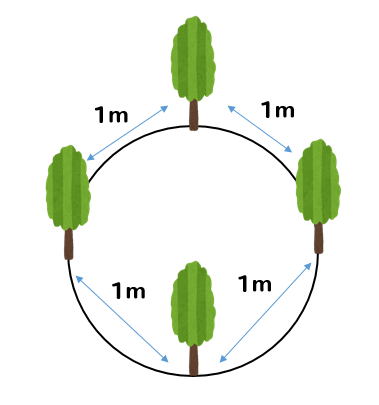
木と木の間は４つできるのに対し、木の本数は4本となります。

つまり、池の周りに木を植える場合には間の数と木の本数が等しくなることが分かります。

植木算まとめ

植木算には３つのパターンがありました。

それぞれの場合においての、木の本数は以下のように求めることができます。

両端に木を植えるとき

$$（木の本数）=（間の数）+1$$

両端に木を植えないとき

$$（木の本数）=（間の数）-1$$

池のまわりに木を植えるとき

$$（木の本数）=（間の数）$$

このような公式を覚えておけば便利ですが

考え方を忘れてしまった場合でも

自分で図を書きながら、木の本数と間の関係性を調べていけば思い出すことができるはずです。

あとは、たくさん問題を解いて理解を深めていきましょう！