今回は平方根の大小関係を表す問題を
パターン別に解説していくよ!
今回紹介していく問題はこちら
次の各組の数の大小を不等号を使って表しなさい。
(1)\(\sqrt{3} ,\sqrt{5}\)
(2)\(-\sqrt{6},-\sqrt{7}\)
(3)\(3,\sqrt{7}\)
(4)\(\sqrt{0.1},0.1\)
(5)\(2\sqrt{3},3\sqrt{2}\)
(6)\(\displaystyle -\frac{1}{3},-\sqrt{\frac{1}{3}}\)
(7)\(5,\sqrt{21},\sqrt{23}\)
(8)\(-\sqrt{35},-6,-\sqrt{37}\)
(9)\(\displaystyle \frac{3}{5},\sqrt{\frac{3}{5}},\frac{\sqrt{3}}{5},\frac{3}{\sqrt{5}}\)
次の条件を満たす\(x\)の値をすべて求めなさい。
(10)\(4<\sqrt{x}<5\)
(11)\(\sqrt{10}<x<\sqrt{50}\)
平方根の大小については、こちらの動画でも解説しています(/・ω・)/

【平方根】大小関係を不等号で表すための予備知識
平方根の大小関係を考えるときに
知っておきたい予備知識がこちら
平方根大小を考えるポイント正の数\(a,b\)で、\(a<b\)ならば
\(\Large \sqrt{a}<\sqrt{b}\) \(,\Large-\sqrt{a}>-\sqrt{b}\)
$$\sqrt{2}<\sqrt{3}$$
$$-\sqrt{2}>-\sqrt{3}$$
ルートのついていない数は、2乗するとルートの形になる。
$$2=\sqrt{2^2}=\sqrt{4}$$
$$2\sqrt{5}=\sqrt{2^2\times 5}=\sqrt{20}$$

【平方根の大小】各問題の答え&解説
それでは、各問題の解説をしていきます。
(1)の解説!
答え
$$\sqrt{3}<\sqrt{5}$$
ルートの中身である3と5の大小関係を考えれば簡単に分かりますね。
\(3<5\)なので、\(\sqrt{3}<\sqrt{5}\)となります。
(2)の解説!
答え
$$-\sqrt{6}>-\sqrt{7}$$
負の数の場合、-6と-7の大小関係を考えます。
\(-6>-7\)なので、\(-\sqrt{6}>-\sqrt{7}\)となります。
(3)の解説!
答え
$$3>\sqrt{7}$$
ルートがついている数とそうでない数を比較するときには
パッと見ではどちらが大きいかを判断することができません。
そのため、3をルートがついた形に変形してやり
$$\Large{3=\sqrt{3^2}=\sqrt{9}}$$
同じルート同士にしてから大小関係を比較しましょう。
\(\sqrt{9}>\sqrt{7}\)なので、\(3>\sqrt{7}\)となります。
(4)の解説!
答え
$$\sqrt{0.1}>0.1$$
小数が出てきても同様に考えていきましょう。
0.1をルートの形に変形してから大小関係を比較します。
$$\Large{0.1=\sqrt{0.1^2}=\sqrt{0.01}}$$
\(\sqrt{0.1}>\sqrt{0.01}\)なので、\(\sqrt{0.1}>0.1\)となります。
(5)の解説!
答え
$$2\sqrt{3}<3\sqrt{2}$$
それぞれルートの形ではありますが
ルートの外に数があるため
大小関係が分かりにくいです…
こういう場合には、ルートの外にある数を中に入れてしまいましょう。
$$\Large{2\sqrt{3}=\sqrt{2^2\times 3}=\sqrt{12}}$$
$$\Large{3\sqrt{2}=\sqrt{3^2\times 2}=\sqrt{18}}$$
そうすることで、大小関係がハッキリとわかるようになりますね(^^)
\(\sqrt{12}<\sqrt{18}\)なので、\(2\sqrt{3}<3\sqrt{2}\)となります。
(6)の解説!
答え
$$\displaystyle -\frac{1}{3}>-\sqrt{\frac{1}{3}}$$
\(\displaystyle -\frac{1}{3}\)をルートの形に変形します。
$$\displaystyle -\frac{1}{3}=-\sqrt{ \left ( \frac{1}{3} \right ) ^2}$$
$$=-\sqrt{ \frac{1}{9}}$$
\(\displaystyle -\frac{1}{9}>-\frac{1}{3}\)だから
\(\displaystyle -\sqrt{\frac{1}{9}}<-\sqrt{\frac{1}{3}}\)なので、\(\displaystyle -\frac{1}{3}>-\sqrt{\frac{1}{3}}\)となります。
(7)の解説!
答え
$$\sqrt{21}<\sqrt{23}<5$$
5をルートの形に変形しましょう。
$$\Large{5=\sqrt{5^2}=\sqrt{25}}$$
そして、3つの数の大小関係を比較するときには
それぞれの数を
小<中<大 に並びかえて表してやります。
\(\sqrt{21}<\sqrt{23}<\sqrt{25}\)なので、\(\sqrt{21}<\sqrt{23}<5\)となります。
(8)の解説!
答え
$$-\sqrt{37}<-6<-\sqrt{35}$$
ー6をルートの形に変形して、それぞれの数の大小関係を比較していきます。
$$\Large{-6=-\sqrt{6^2}=-\sqrt{36}}$$
\(-\sqrt{37}<-\sqrt{36}<-\sqrt{35}\)なので、\(-\sqrt{37}<-6<-\sqrt{35}\)となります。
(9)の解説!
答え
$$\frac{\sqrt{3}}{5}<\frac{3}{5}<\sqrt{\frac{3}{5}}<\frac{3}{\sqrt{5}}$$
それぞれの数をルートの数に変形して、大小関係を比較していきましょう。
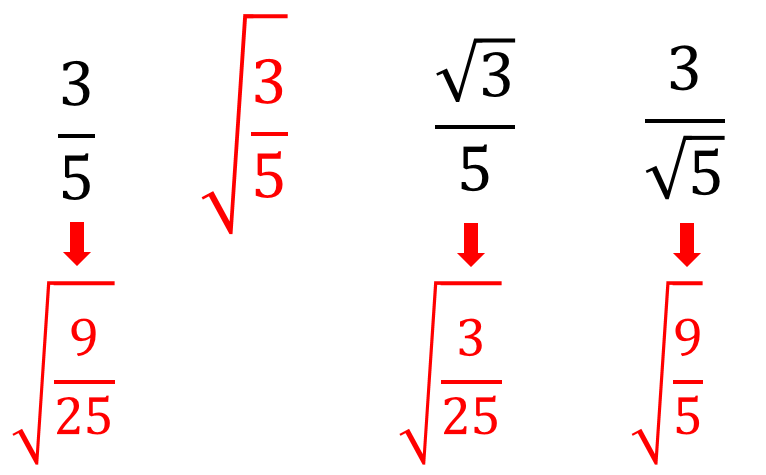
全てルートの形に変形できたら
ルートの中身を通分してやることで
大小関係が分かりやすくなります。
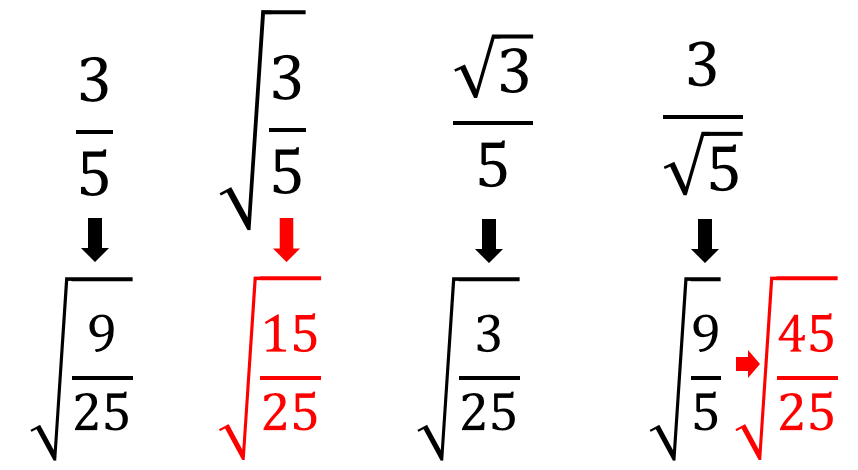
よって
$$\frac{\sqrt{3}}{5}<\frac{3}{5}<\sqrt{\frac{3}{5}}<\frac{3}{\sqrt{5}}$$
となります。
(10)の解説!
(10)\(4<\sqrt{x}<5\)
答え
$$17,18,19,20,21,22,23,24$$
4と5をルートの形にして\(x\)の範囲を求めていきます。
$$\sqrt{16}<\sqrt{x}<\sqrt{25}$$

よって、条件を満たす\(x\)は
17,18,19,20,21,22,23,24となります。
(11)の解説!
(11)\(\sqrt{10}<x<\sqrt{50}\)
答え
$$4,5,6,7$$
\(x\)をルートの形に変形します。
$$x=\sqrt{x^2}$$
すると
\(\sqrt{10}<\sqrt{x^2}<\sqrt{50}\)となるので
\(10<x^2<50\)を満たす\(x\)の範囲を考えれば良いことになります。
10から50の間の数で
ある数の2乗になっているのは

\(4^2=16\)
\(5^2=25\)
\(6^2=36\)
\(7^2=49\)
ということで
答えは4,5,6,7となります。
ルートの大小まとめプリントを用意しました!
さて、いろんなパターンを紹介しましたがしっかりと理解できましたか?
記事を読んでいると「ふむふむ…」と納得した気になりますが、いざ問題にチャレンジしてみると「…(どうやるんだっけ?)」となることもあります(^^;)
テストでしっかりと得点するためには反復演習を通して理解を深めることが大事!
というわけで、今回はルートの大小についてのまとめ演習課題を用意しました。
動画解説もつけているので、ややこしいところも完璧に理解できるはずです!次の試験で+10点を目指してチャレンジしてみましょう(‘ω’)ノ
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
【演習課題】ルートの大小
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
【平方根の大小】 まとめ
お疲れ様でした!
平方根の大小関係を比べるときには
それぞれの数をルートの形に変形して
中身の大小を比較してやります。
入試では(10)(11)のような
範囲を与えられる問題が多いですが
考え方は非常にシンプルです。
ルートに変形して、中身を比べる!
それだけですね(^^)
あとは練習あるのみ!
たくさん練習して、平方根の大小関係をマスターしましょう。
ファイトだー(/・ω・)/
ルートとは?平方根の求め方を解説!分数や小数の場合はどうやる?
平方根の大小関係を不等号で表す問題を解説!←今回の記事


















コメントを残す