今回は小学生の算数で学習する
『立方体の体積』
について学習していこう！
立方体の体積公式って？
あれ、そもそも立方体と直方体って何が違う？
立方体の体積問題を解いてみよう！
という流れで解説していくよ(^^)
立方体の体積公式
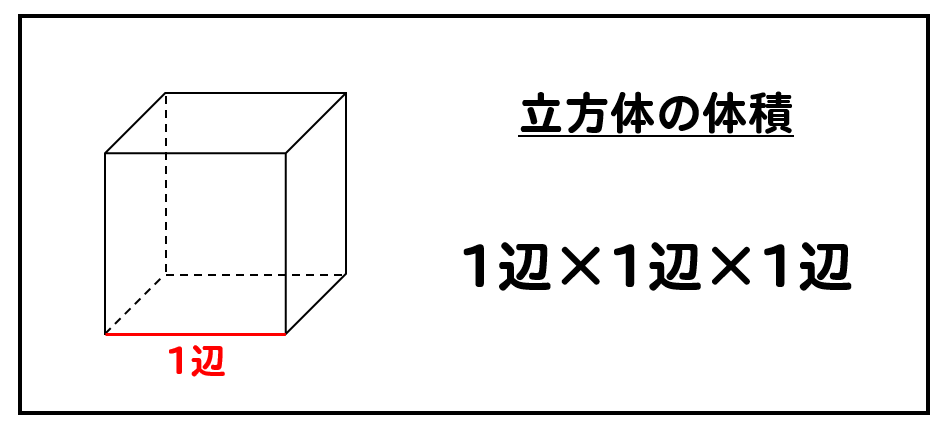
立方体の体積は至ってシンプル！
1辺の長さを3回掛けるだけだ！
1辺というのは、どこの辺でもOK
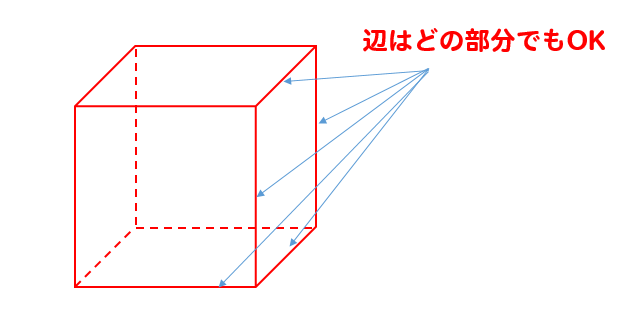
立方体というのは、ぜーんぶ辺の長さが同じだったよね。
だから、辺はどこを見てもらってもいいよ！
あれ？
でも、立方体って直方体の体積と同じように
（たて）×（よこ）×（高さ）
これじゃダメなのかな？
そんな疑問を抱く人もいるでしょう。
というわけで次は立方体と直方体の違いについてみておきましょう。
立方体と直方体って何が違う？
立方体と直方体の違いってなんぞ？
これね、答えに戸惑っちゃう人多いよね
立方体というのは、６つの正方形によって囲まれた立体。
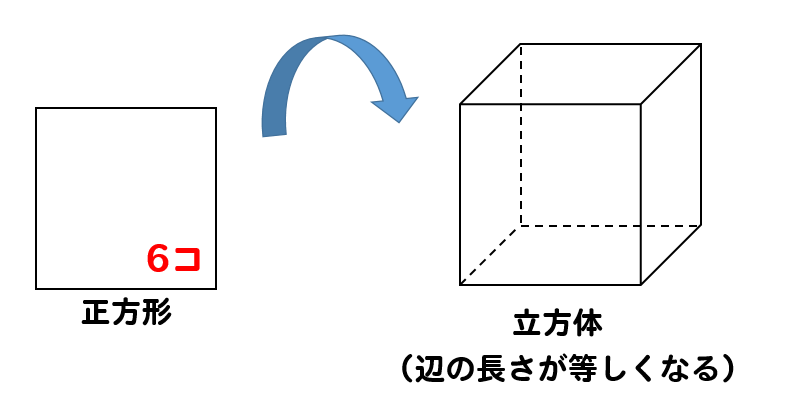
つまり、辺の長さが全部同じになるってことだね。
サイコロのような形になっています。
直方体とは、長方形または正方形によって囲まれた立体。
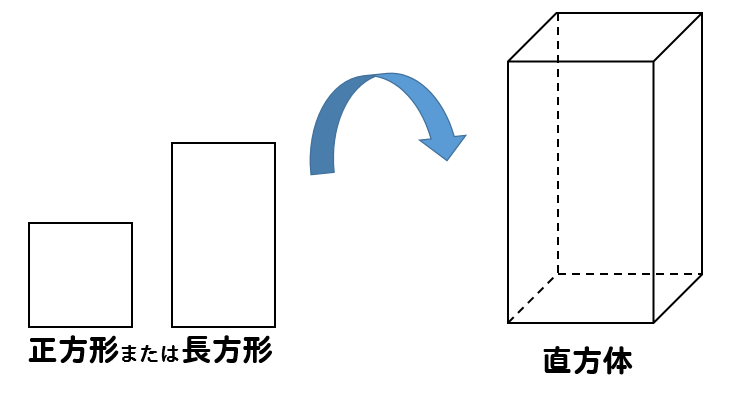
つまり、同じ長さになっているところもあれば違うところもあるってことだね。
箱のような形になっています。
そして、立方体と直方体には次のような関係があります。
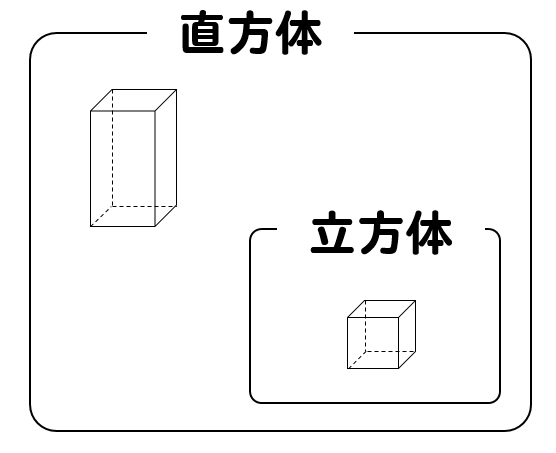
直方体という大きなグループの中で
全部の面が正方形によって囲まれている特別なヤツ
それが立方体というモノなのです。
なので、立方体も直方体の仲間ということになります。
だから、立方体も直方体の公式と同じく
（たて）×（よこ）×（高さ）
で求めることができます。
だけど、立方体の場合
全部の長さが等しくなっちゃうから
それぞれの部位を区別する必要なくね？
ってことで、1辺という表し方になっています。
立方体と直方体
それぞれの公式において、表記はちょっと違うんだけど
言ってる意味は同じだから惑わされないようにしてね！
立方体の体積問題を解説！
それでは、立方体の体積を求める問題に挑戦してみましょう。
次の立方体の体積を求めましょう。
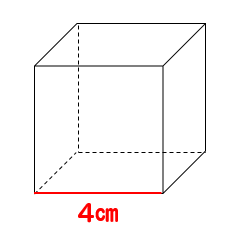
1辺を3回掛ければいいので
$$\Large{4\times 4\times 4=64(cm^3)}$$
となります。
簡単すぎですね！
体積が125㎤になる立方体の1辺の長さを求めましょう。
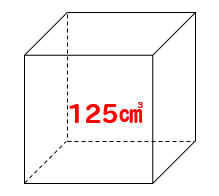
3回掛けて、125になる数を見つければ良いですね。
$$2\times 2\times 2=8$$
$$3\times 3\times 3=27$$
$$4\times 4\times 4=64$$
$$5\times 5\times 5=125$$
順に掛け算をして、探していくと見つかりますね。
答えは5㎝となります。
まとめ
お疲れ様でした！
立方体の体積は
（1辺）×（1辺）×（1辺）
で求めることができます。
だけど、これは直方体の
（たて）×（よこ）×（高さ）
これと全く同じものです。
全ての辺が同じ長さになってしまう立方体では、辺の区別をつけず
たて、よこ、高さのそれぞれを1辺と表しただけです。
以上！
とっても簡単な公式だから
忘れないように覚えておこうね(/・ω・)/
高校入試で使える公式集をプレゼント！
高校入試で使える公式をまとめた教材を作成しました！
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/
これは知らないと損をするかも…！？
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
こちらから公式集を無料で手に入れちゃってください！
ご登録いただいたメールアドレスに教材を送らせていただきます。
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)
コメントを残す