今回は、文字式の単元から
数量の表し方・関係を表す式についてまとめていきます。
パターン別によく出題される問題を紹介しているので、テスト前などの確認にお役立てください(^^)
数量の表し方
代金について
1本\(a\)円の鉛筆を、6本買ったときの代金
$$6a(円)$$
解説はこちら
(代金)=(金額)×(個数)で求めることができるので
$$a\times 6=6a$$
と表すことができます。
1個\(x\)円のみかん4個と1個\(y\)円のりんご5個買ったときの代金
$$4x+5y(円)$$
解説はこちら
みかんの代金は\(x\times 4=4x(円)\)
りんごの代金は\(y\times 5=5y(円)\)
よって、代金の合計は\(4x+5y(円)\)と表すことができます。
1冊130円のノートを\(x\)冊買って、1000円払ったときのおつり
$$1000-130x(円)$$
解説はこちら
(おつり)=(払った金額)ー(代金)で求めることができます。
ノートの代金は\(130 \times x=130x(円)\)であるから
おつりは\(1000-130x(円)\)と表すことができます。
【文字式】おつりを文字で表す方法について解説!
個数、量について
1個の重さが\(a\)gの品物7個を重さ\(b\)gの箱に入れたときの全体の重さ
$$7a+b(g)$$
解説はこちら
\(a\)gが7個あるので、品物の重さは\(a\times 7=7a(g)\)
品物と箱の合計の重さは\(7a+b(g)\)と表すことができます。
\(x\)mLのジュースを、5つの容器に等分したときの容器1つ分の量
$$\frac{x}{5}(mL)$$
解説はこちら
等分する場合には割り算を利用します。
\(x\)を5等分するということなので\(\displaystyle x\div 5=\frac{x}{5}(mL)\)と表すことができます。
長さ80㎝のひもから\(a\)cmのひもを5本切りとるときの残りのひもの長さ
$$80-5a(cm)$$
解説はこちら
\(a\)cmのひもを5本切り取るので、全体として\(a\times 5=5a(cm)\)切り取ることになります。
よって、ひもの残りは全体の長さから切り取った分を引いて\(80-5a(cm)\)と表すことができます。
整数、数について
十の位が\(x\)、一の位が\(y\)の2けたの数
$$10x+y$$
解説はこちら
十の位が\(x\)⇒\(10\times x=10x\)
一の位が\(y\)⇒\(1\times y=y\)
これらを合わせて\(10x+y\)と表せます。単位はつけなくてOKですね。
百の位が\(x\)、十の位が\(y\)、一の位が\(5\)の3けたの数
$$100x+10y+5$$
解説はこちら
百の位が\(x\)⇒\(100\times x=100x\)
十の位が\(y\)⇒\(10\times y=10y\)
一の位が\(5\)⇒\(1\times 5=5\)
これらを合わせて\(100x+10y+5\)と表せます。単位はつけなくてOKですね。
\(a\)と\(b\)の和の4倍
$$4(a+b)$$
解説はこちら
\(a\)と\(b\)を足してから4倍をするということなので
\((a+b)\times 4=4(a+b)\)と表すことができます。単位はつけなくてOK!
5で割ると商が\(a\)で余りが4となる整数
$$5a+4$$
解説はこちら
$$(割られる数)=(割る数)\times (商)+(余り)$$
よって、\(5\times a +4=5a+4\)と表すことができます。
平均について
数学のテストで、2人が\(a\)点、3人が\(b\)点であったとき、この5人の平均点
$$\frac{2a+3b}{5}(点)$$
解説はこちら
$$(平均点)=\frac{(合計点)}{(人数)}$$
まずは、合計点を文字を使って表すと\(2\times a+3\times b=2a+3b\)となります。
よって、平均点は\(\displaystyle \frac{2a+3b}{5}(点)\)と表すことができます。
10人が受けた数学のテストの結果は、全体の平均点が\(a\)点で、女子3人の平均点が\(b\)点であった。このときの、男子7人の平均点
$$\frac{10a-3b}{7}(点)$$
解説はこちら
$$(合計点)=(平均点)\times (人数)$$
10人が受けた数学のテストの合計点は\(a\times 10=10a(点)\)
女子3人の合計点は\(b\times 3=3b(点)\)と表せます。
よって、男子の合計点は\(10a-3b(点)\)となるので
男子の平均点は\(\displaystyle \frac{10a-3b}{7}(点)\)と表すことができます。
速さについて
時速30㎞で、\(x\)時間進んだときの道のり
$$30x(km)$$
解説はこちら
$$(道のり)=(速さ)\times (時間)$$
よって、\(30\times x=30x(km)\)と表すことができます。
\(x\)㎞の道のりを\(3\)時間で進んだときの速さ
$$時速\frac{x}{3}(km)$$
解説はこちら
$$(速さ)=\frac{(道のり)}{(時間)}$$
よって、\(\displaystyle 時速\frac{x}{3}(km)\)と表すことができます。
20mの道のりを分速\(a\)mで進んだときにかかる時間
$$\frac{20}{a}(分)$$
解説はこちら
$$(時間)=\frac{(道のり)}{(速さ)}$$
よって、\(\displaystyle \frac{20}{a}(分)\)と表すことができます。
\(a\)kmはなれた隣町まで、行きは時速4㎞、帰りは時速5㎞の速さで歩くときの往復にかかる時間
$$\frac{a}{4}+\frac{a}{5}(時間) もしくは\frac{9}{20}a(時間)$$
解説はこちら
行きにかかる時間は\(\displaystyle \frac{a}{4}\)
帰りにかかる時間は\(\displaystyle \frac{a}{5}\)
よって、往復にかかる時間は\(\displaystyle \frac{a}{4}+\frac{a}{5}(時間)\)と表せます。
文字式の計算を習った方は\(\displaystyle \frac{a}{4}+\frac{a}{5}=\frac{9}{20}a(時間)\)まで計算しておきましょう。
家から\(a\)km離れた公園に向かって、時速5㎞で歩くとき、出発してから\(b\)時間後の残りの道のり
$$a-5b(km)$$
解説はこちら
時速5㎞で\(b\)時間進んだときの道のりは\(5b(km)\)
よって、残りの道のりは\(a-5b(km)\)と表せます。
速さについては、こちらの記事でも詳しく解説しています。
>>>【文字式】速さの表し方はこれでバッチリ!
割合について
\(x\)円の7%の金額
$$\frac{7}{100}x(円) もしくは 0.07x(円)$$
解説はこちら
7% ⇒ \(\displaystyle \frac{7}{100}\)
よって、\(\displaystyle x \times \frac{7}{100}=\frac{7}{100}x(円)\)
\(x\)円の3割の金額
$$\frac{3}{10}x(円) もしくは 0.3x(円)$$
解説はこちら
3割 ⇒ 30% ⇒ \(\displaystyle \frac{30}{100}=\frac{3}{10}\)
よって、\(\displaystyle x \times \frac{3}{10}=\frac{3}{10}x(円)\)
\(x\)円の20%引きの金額
$$\frac{4}{5}x(円) もしくは 0.8x(円)$$
解説はこちら
20%引き ⇒ 80% ⇒ \(\displaystyle \frac{80}{100}=\frac{4}{5}\)
よって、\(\displaystyle x \times \frac{4}{5}=\frac{4}{5}x(円)\)
\(x\)gの10%増量した重さ
$$\frac{11}{10}x(g) もしくは 1.1x(g)$$
解説はこちら
10%増 ⇒ 110% ⇒ \(\displaystyle \frac{110}{100}=\frac{11}{10}\)
よって、\(\displaystyle x \times \frac{11}{10}=\frac{11}{10}x(g)\)
1000円の\(x\)%引きの金額
$$1000-10x(円)$$
解説はこちら
\(x\)% ⇒ \(\displaystyle \frac{x}{100}\)
よって、1000円の\(x\)%は\(\displaystyle 1000 \times \frac{x}{100}=10x(円)\)
1000円の\(x\)%引きの金額は\(1000-10x\)(円)と表すことができます。
割合については、こちらの記事でも詳しく解説しています。
>>>【文字式】割合の表し方はこれでバッチリ!

図形・公式について
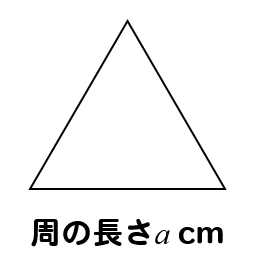
周の長さが\(a\)cmである正三角形の1辺の長さ

$$\frac{a}{3}(cm)$$
解説はこちら
正三角形は3つの辺があるので、1辺の長さは周の長さを3等分したものになります。
よって、\(\displaystyle a\div 3=\frac{a}{3}(cm)\)となります。
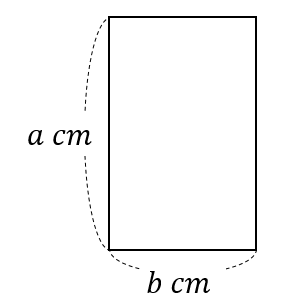
縦\(a\)cm、横\(b\)cmである長方形の周の長さ

$$2(a+b)(cm)$$
解説はこちら
長方形の周の長さは、縦の長さ2つ分と横の長さ2つ分を合わせた長さになります。
よって、\(a\times 2 + b\times 2=2(a+b)(cm)\)と表すことができます。
縦\(a\)cm、横\(b\)cmである長方形の面積

$$ab(cm^2)$$
解説はこちら
(長方形の面積)=(縦の長さ)×(横の長さ)
よって、\(a\times b=ab(cm^2)\)と表すことができます。
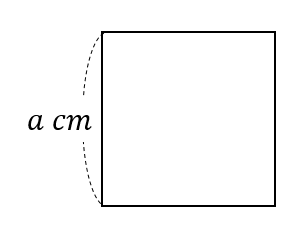
1辺\(a\)cmである正方形の面積

$$a^2(cm^2)$$
解説はこちら
(正方形の面積)=(1辺の長さ)×(1辺の長さ)
よって、\(a\times a=a^2(cm^2)\)と表すことができます。
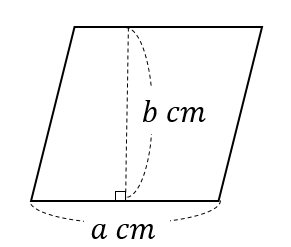
底辺\(a\)cm、高さ\(b\)cmである平行四辺形の面積

$$ab(cm^2)$$
解説はこちら
(平行四辺形の面積)=(底辺の長さ)×(高さ)
よって、\(a\times b=ab(cm^2)\)と表すことができます。
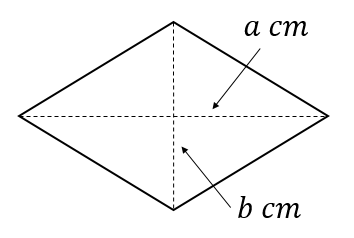
対角線が\(a\)cm、\(b\)cmであるひし形の面積

$$\frac{ab}{2}(cm^2)$$
解説はこちら
(ひし形の面積)=(対角線の長さ)×(対角線の長さ)×\(\displaystyle \frac{1}{2}\)
よって、\(\displaystyle a\times b\times \frac{1}{2}=\frac{ab}{2}(cm^2)\)と表すことができます。
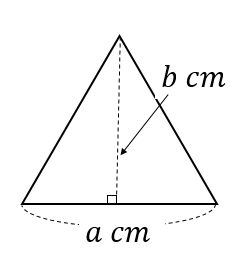
底辺\(a\)cm、高さ\(b\)cmである三角形の面積

$$\frac{ab}{2}(cm^2)$$
解説はこちら
(三角形の面積)=(底辺の長さ)×(高さ)×\(\displaystyle \frac{1}{2}\)
よって、\(\displaystyle a\times b\times \frac{1}{2}=\frac{ab}{2}(cm^2)\)と表すことができます。
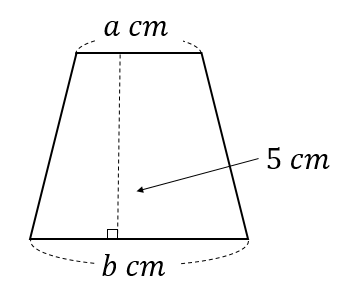
上底\(a\)cm、下底\(b\)cm、高さ5㎝である台形の面積

$$\frac{5(a+b)}{2}(cm^2)$$
解説はこちら
(台形の面積)={(上底の長さ)+(下底の長さ)}×(高さ)×\(\displaystyle \frac{1}{2}\)
よって、\(\displaystyle (a+b)\times 5\times \frac{1}{2}=\frac{5(a+b)}{2}(cm^2)\)と表すことができます。
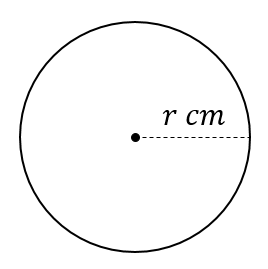
半径\(r\)cmである円の円周の長さ
(ただし、円周率は\(\pi\)とする)

$$2\pi r(cm)$$
解説はこちら
$$(円周の長さ)=2\times (半径)\times (円周率\pi)$$
よって、\(2\times r \times \pi=2\pi r(cm)\)と表すことができます。
半径\(r\)cmである円の面積
(ただし、円周率は\(\pi\)とする)

$$\pi r^2(cm^2)$$
解説はこちら
$$(円の面積)=(半径)\times (半径)\times (円周率\pi)$$
よって、\(r\times r \times \pi=\pi r^2(cm^2)\)と表すことができます。
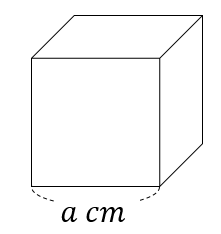
1辺が\(a\)cmの立方体の体積

$$a^3(cm^3)$$
解説はこちら
$$(立方体の体積)=(1辺)\times (1辺)\times (1辺)$$
よって、\(a \times a \times a=a^3(cm^3)\)となります。
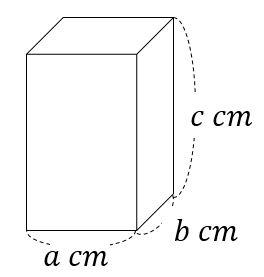
横\(a\)cm、縦\(b\)cm、高さ\(c\)cmの直方体の体積

$$abc(cm^3)$$
解説はこちら
$$(直方体の体積)=(横)\times (縦)\times (高さ)$$
よって、\(a \times b \times c=abc(cm^3)\)となります。
単位の変換
\(x\)mを㎝の単位で表せ
$$100x(cm)$$
解説はこちら
\(1m=100cm\)より、mから㎝に変換するためには\(\times 100\)すればよいことがわかる。
よって、\(x\times 100=100x(cm)\)と表すことができます。
\(a\)gをkgの単位で表せ
$$\frac{a}{1000}(kg)$$
解説はこちら
\(1kg=1000g\) ⇒ \(\displaystyle 1g=\frac{1}{1000}kg\)
gからkgに変換するためには\(\displaystyle \times \frac{1}{1000}\)すればよいことがわかる。
よって、\(\displaystyle a \times \frac{1}{1000}=\frac{a}{1000}(kg)\)と表すことができます。
\(a\)分を時間の単位で表せ
$$\frac{a}{60}(時間)$$
解説はこちら
\(1時間=60分\) ⇒ \(\displaystyle 1分=\frac{1}{60}時間\)
分から時間に変換するためには\(\displaystyle \times \frac{1}{60}\)すればよいことがわかる。
よって、\(\displaystyle a \times \frac{1}{60}=\frac{a}{60}(時間)\)と表すことができます。
\(a\)dLをLの単位で表せ
$$\frac{a}{10}(L)$$
解説はこちら
\(1L=10dL\) ⇒ \(\displaystyle 1dL=\frac{1}{10}L\)
dLからLに変換するためには\(\displaystyle \times \frac{1}{10}\)すればよいことがわかる。
よって、\(\displaystyle a \times \frac{1}{10}=\frac{a}{10}(L)\)と表すことができます。
関係を表す式
等号を使った式
\(x\)の5倍は\(y\)より4だけ大きい
$$5x=y+4$$
解説はこちら
\(x\)の5倍 ⇒ \(5x\)
\(y\)より4大きい数 ⇒ \(y+4\)
それぞれが等しくなるので\(5x=y+4\)と表すことができます。
1冊\(x\)円の本3冊と1本\(y\)円の鉛筆4本を買ったときの代金の合計は600円だった。
$$3x+4y=600$$
解説はこちら
1冊\(x\)円の本3冊と1本\(y\)円の鉛筆4本を買ったときの代金 ⇒ \(3x+4y\)
代金 ⇒ 600円
それぞれが等しくなるので\(3x+4y=600\)と表すことができます。
1冊\(x\)円の本4冊買い、3000円を出したところ、おつりは\(y\)円だった。
$$y=3000-4x$$
解説はこちら
1冊\(x\)円の本4冊買ったときの代金 ⇒ \(4x\)
3000円出したときのおつり ⇒ \(3000-4x\)
おつり ⇒ \(y\)円
それぞれが等しくなるので\(y=3000-4x\)と表すことができます。
\(x\)kmの道のりを時速4㎞の速さで歩いたところ、\(y\)時間かかった。
$$y=\frac{x}{4}$$
解説はこちら
\(x\)kmの道のりを時速4㎞の速さで歩いた時間 ⇒ \(\displaystyle \frac{x}{4}\)
かかった時間 ⇒ \(y\)時間
それぞれが等しくなるので\(\displaystyle y=\frac{x}{4}\)と表すことができます。
\(a\)本の鉛筆を1人に6本ずつ\(b\)人に配ると、3本足りない。
$$a=6b-3$$
解説はこちら
1人に6本ずつ\(b\)人に配ると、3本足りない ⇒ \(6b-3\)
鉛筆の本数 ⇒ \(a\)本
それぞれが等しくなるので\(a=6b-3\)と表すことができます。
不等号を使った式
\(x\)の3倍は、\(y\)に4を加えた数以上である。
$$3x≧y+4$$
解説はこちら
\(x\)の3倍 ⇒ \(3x\)
\(y\)に4を加えた数 ⇒ \(y+4\)
(\(x\)の3倍)≧(\(y\)に4を加えた数)
よって、\(5x=y+4\)と表すことができます。
1本\(x\)円の鉛筆を7本買っても、代金は600円未満である。
$$7x<600$$
解説はこちら
1本\(x\)円の鉛筆を7本買った代金 ⇒ \(7x\)
(1本\(x\)円の鉛筆を7本買った代金)<(600)
よって、\(7x<600\)と表すことができます。
1冊\(x\)円のノート4冊と、1本\(b\)円のペンを7本買い、1000円札を出したら、買うことができた。
$$4x+7b≦1000$$
解説はこちら
1冊\(x\)円のノート4冊と、1本\(b\)円のペンを7本買った代金 ⇒ \(4x+7b\)
1000円で買うことができたということは、代金は1000円以下だったことを表しています。
よって、(代金)≦(1000)
よって、\(4x+7b≦1000\)と表すことができます。
まとめ
お疲れ様でした!
数量、関係を表す式はいろんなパターンがありますね。
特に速さや割合については、方程式の文章問題でもよく活用されるのでしっかりと身につけておきたいです。
このページで1度学習した人は、今後もテスト前にはこのページを活用して文字式の表し方を確認するようにしてみてくださいね!
文字式の文章題について理解を深めたら、次は計算をしっかりとマスターしておきましょう。
>【中1文字式】計算のやり方を1から丁寧に!
>【文字式】分数の計算問題を1から丁寧に!





















とてもためになりました
自分がわからない表し方が解説でよく分かりました!
分からなかった単位の変換がわかりました!
ありがとうございます!
それはよかったです!!
単位変換はちょっと難しいですが、
これが解けるようになると強いですね!