【中学】相対度数の計算方法と問題はこれでバッチリ！

今回は中1で学習する資料の活用という単元から

相対度数の計算方法について解説していくよ！

 

相対度数のテーマとしてはこんな感じです。

累積相対度数っていうのは、中学では習わないかもしれませんが簡単なことなので高校準備ということで知っておいても損はないですよ(^^)

では、相対度数について一緒に学んでいきましょー！

 

 

相対度数とは

各階級の度数が、全体の中でどれだけの割合にあたるかを示す値を相対度数といいます。

そして、このように（求めたい階級の度数）÷（度数の合計）を計算することで相対度数を求めることができます。

 

相対度数の計算方法と表し方

それでは、どのように相対度数を求めればよいのか具体例を交えて解説していきます。

次の資料を見て、各階級の相対度数を求めてみましょう。

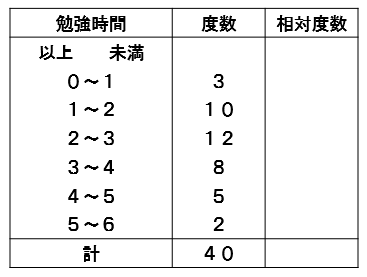
0以上1未満の階級の度数は3ですね。

だから、相対度数は

$$\LARGE{\frac{3}{40}}$$

$$\LARGE{=3\div 40}$$

$$\LARGE{=0.075}$$

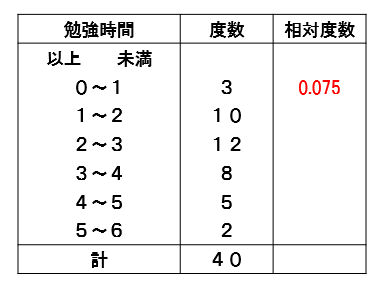
このように相対度数を求めることができます。

他の階級についても同様ですね。

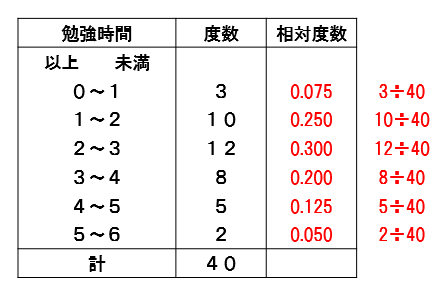
このように求めることができます。

 

ポイントとしては

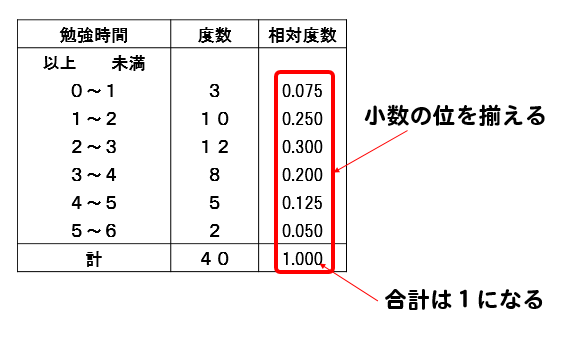
相対度数は、小数の位を揃えて表します。

2以上3未満の階級では\(12\div 40=0.3\)となるのですが、他の階級の相対度数に合わせて小数第3位まで表し、\(0.300\)としてやりましょう。

 

また、すべての階級の相対度数を合わせると1になります。

もしも１にならなければ、どこかが計算ミスしていることになるので問題を解くときには、ちゃんと確かめるようにしましょう。

相対度数は分数から小数の形にする

上でも解説しましたが、相対度数は分数ではなく小数の形で答えるようにしましょう。

分数でも間違っているわけではないのですが、すべて小数に変換しておいた方が数値を扱う上で便利になります。

 

例えば、分数の形で表していると

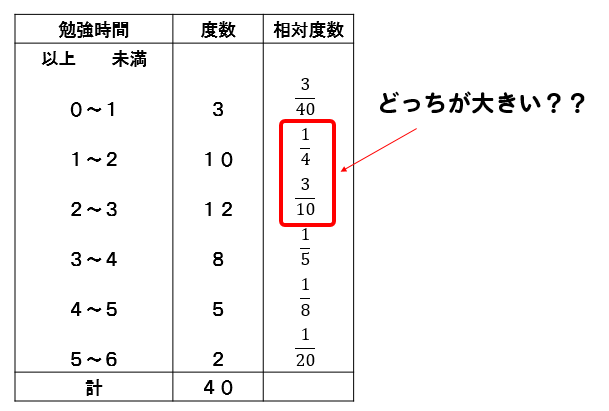
パッと見た感じで、どっちが大きいかっていうのが判断しにくいよね。

 

 

だけど、小数なら

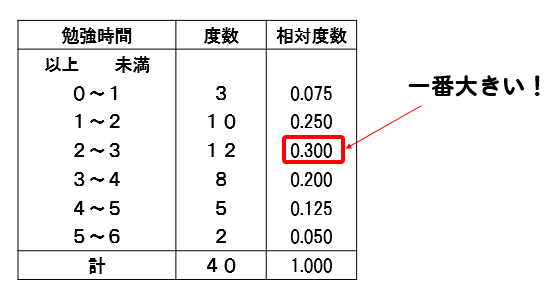
パッと見た感じで、数値の大小が分かりやすい！！

ということで、数値は分かりやすい方が便利なので相対度数は小数で表すようにしましょう。

 

相対度数の単位ってなに？？

相対度数に単位はつけません！

相対度数というのは、割合を表す数値です。

 

人数を扱っているデータだからといって

相対度数は0.200人とはなりませんので気をつけてください。

 

相対度数の答え方は

0.200

というように単位をつけなくてOKです。

 

相対度数から度数を求める

相対度数を用いると、その階級の度数を求めることができます。

 

以下のように、相対度数は分かっているんだけど度数が分からないというような場合

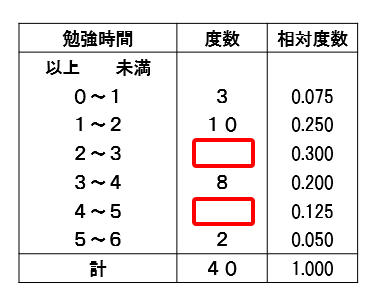
2以上3未満の階級の度数は

$$\LARGE{40\times 0.300}$$

$$\LARGE{=12}$$

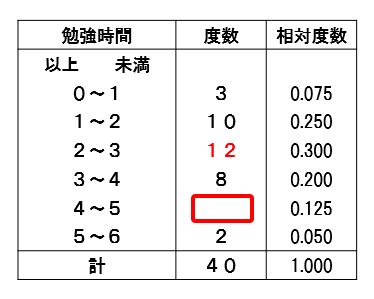
このように求めることができます。

 

 

4以上5未満の階級の度数は

$$\LARGE{40\times 0.125}$$

$$\LARGE{=5}$$

と求めることができますが、他の階級の度数がすべて分かっている状況では度数の合計を見て判断する方が簡単ですね。

 

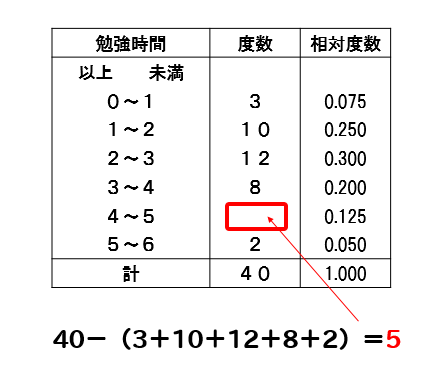
このように、相対度数を用いて階級の度数を求めさせる問題もあります。

相対度数の求め方だけではなく、度数を求める方法についてもしっかりと覚えておきましょう。

 

ヒストグラムから相対度数を求める

先ほどは資料の度数分布表を見ながら、相対度数を求めましたがヒストグラムを見ながらでも相対度数は求めることができます。

以下のヒストグラムを見ながら1時間の階級の相対度数を求めてみましょう。

 

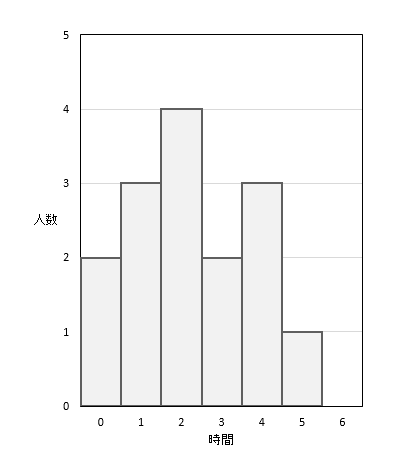
まず、全体の度数を求めると

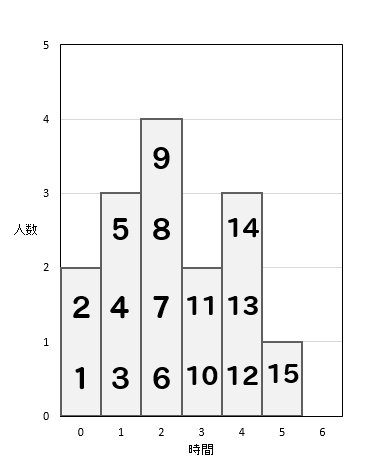
全体の度数は15だということが読み取れます。

そして、1時間の度数は3であることも読み取れるので

相対度数は

$$\LARGE{\frac{3}{15}}$$

$$\LARGE{=3\div15}$$

$$\LARGE{=0.2}$$

と、求めることができます。

 

ヒストグラムから相対度数を求める場合には

全体の度数と、その階級の度数を読み取る必要があります。

 

というか、ただ数えれば良いだけなので難しくはありませんね(^^;

ヒストグラムが出てきても落ち着いて回答してください！

 

相対度数と累積相対度数の違いとは

累積相対度数ってなんじゃ？

なんか聞きなれない言葉だと思いますが、高校生の試験などではちょこちょこと目にします。

そんなに難しい話ではないので、中学生の方も知識として持っておいても良いかと思います。

 

累積相対度数とは、相対度数をはじめの階級からその階級まで足したものです。

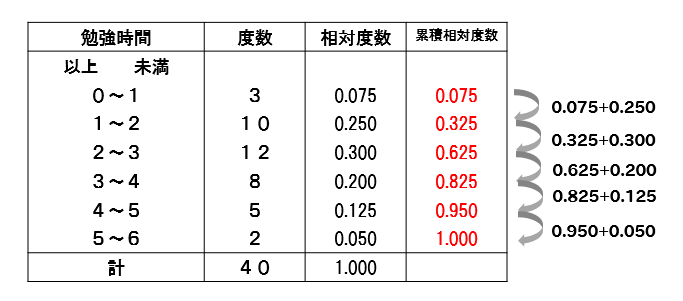
このように、各階級の相対度数を順に累積させていった数値のことを累積相対度数といいます。

 

累積相対度数の利点とは？

そもそも累積相対度数って、どんな利点があるの？

どんな場面で使うの？ってことになるよね。

では、上で扱った資料の相対度数と累積相対度数をそれぞれ折れ線グラフにしたものを見てみましょう。

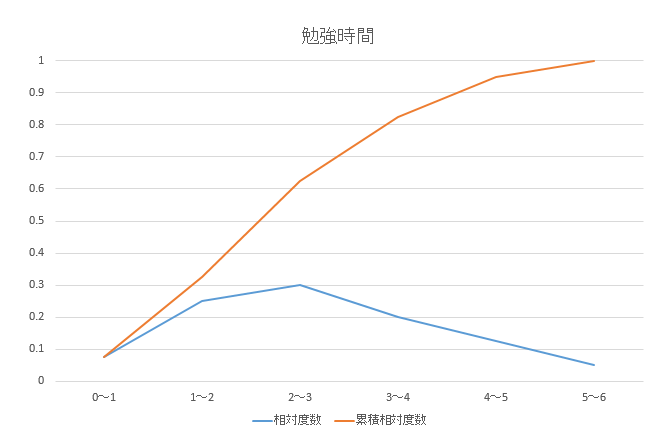
青色の折れ線が相対度数

相対度数は各階級の割合を表しているので、ジグザグした形になっています。

このグラフを見れば、どの階級が多いのかが一目瞭然ですね。

一番とんがっている2～3時間の人が多いんだなーってことが分かりやすいです。

 

 

 

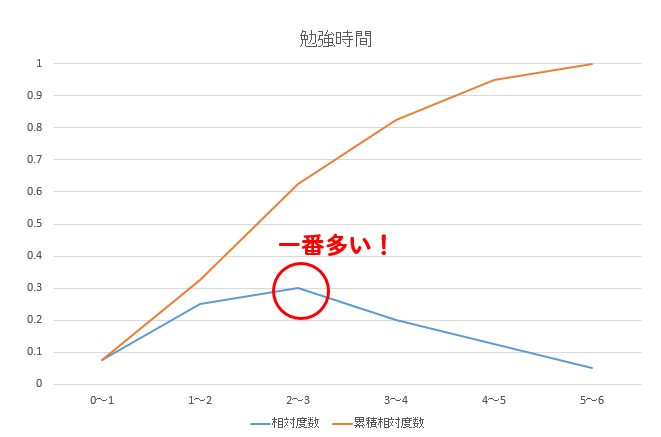
そして、オレンジの折れ線が累積相対度数です。

こちらは相対度数がどんどん累積されていくので、ジグザグというよりも右上がりなグラフになっています。

こちらは、ここまでの階級が全体のどれくらいの割合になっているのかを読み取るのに適しています。

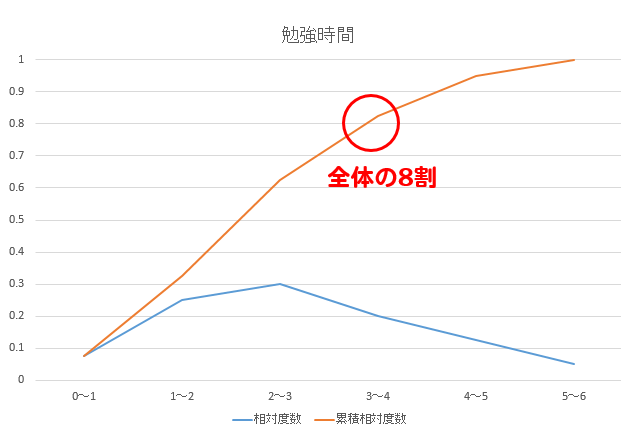
このグラフから勉強時間が0～4時間の人が全体の8割を超えていることが読み取れます。

 

 

このように、各階級の割合やそれぞれの階級を比較したい場合には相対度数。

ここまでの階級が全体のどれくらいの割合なのかを考えたい場合には累積相対度数。

 

というようにそれぞれの利点を生かして、より便利な方を活用していくようになります。

 

練習問題に挑戦！

それでは、相対度数に関する問題に挑戦してみましょう！

 

 

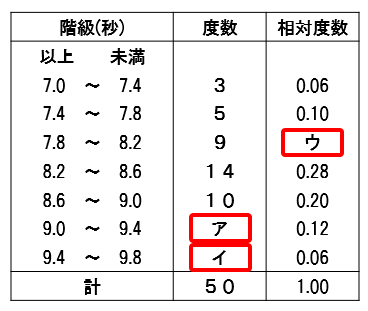
【追加】試験によく出るパターンはこの４つ！

資料の活用を学習している数スタ読者のみなさんへ！

この単元で得点UPを目指すのであれば「相対度数」「中央値」「最頻値」「ヒストグラムの読み取り」、この4パターンを習得しておきましょう。（僕が教えている学生さんから定期テストの過去問などを見せてもらうと、これらは必ず出題されています！）

 

それぞれは簡単なものなのですが、試験になるとちょっとひねった形で出題されることもあるので…

不安なく試験に挑めるよう「どういった形でテストに出てくるのか」を知っておくための演習課題を用意しました。定期テストや入試過去問から抜粋したので、これらがしっかりと解けていればバッチリかな＾＾

というわけで、この単元での点数アップを狙いたいのであれば、こちらの演習にもチャレンジしてみてください(‘ω’)ノ

今回の演習課題には動画解説もつけています。

数学が苦手な方でも動画を見ながら最後までやり切ることができますよ＾＾

 

 

この課題を活用してみたい！という方にはメールでプリントを送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので、ぜひご活用ください＾＾

 

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

相対度数について、覚えておきたいのは

この２点です。

 

これを覚えておければ、問題を解くことは簡単です。

そんなに難しい問題は出題されないので、試験では得点源にできるはずですよ(^^)

たくさん練習して、しっかりと身につけておきましょう。

ファイトだー(/・ω・)/