その文字に着目したときの係数と次数をいえ。
また、定数項は何か?
高校数学の1発目の学習が今回取りあげる次数、係数のお話になります。
も、文字に着目!?と面食らってしまう方もいるかもしれませんが、簡単なことなのでサクッと理解しちゃいましょう♪
サクッと理解したい方はこちらをどうぞ!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
文字に着目したときの次数と係数とは(単項式)
簡単に復習しておきましょう。
次数とは、文字の個数。
係数とは、文字にかけられている数のことでしたね。
例えば、\(-5ab^2\)という式であれば
ということで、文字は\(a\)が2個、\(b\)が1個、合計で文字は3個だから、次数は3。
そして、文字にかけられている数は\(-5\)だから、係数は\(-5\)ということになります。
この辺を忘れちゃったという方は、こちらの記事または動画で復習しておいてください。
では、ここから「文字に着目する」という高校内容に入りましょう。
\(x\)に着目するとき、その次数と係数をいえ。
$$2ab^2x^3$$
文字に着目するとは、その文字以外を数だと考えろ!
ということです。
ん、何言ってんだ?って感じかもしれませんがw
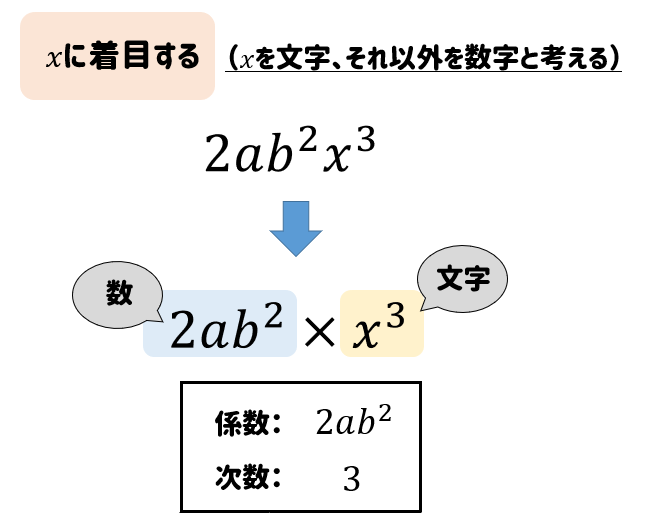
こんな感じですね。
次のように、2つの文字に着目する場合もあります。
\(x\)と\(y\)に着目するとき、その次数と係数をいえ。
$$-2x^2yz$$
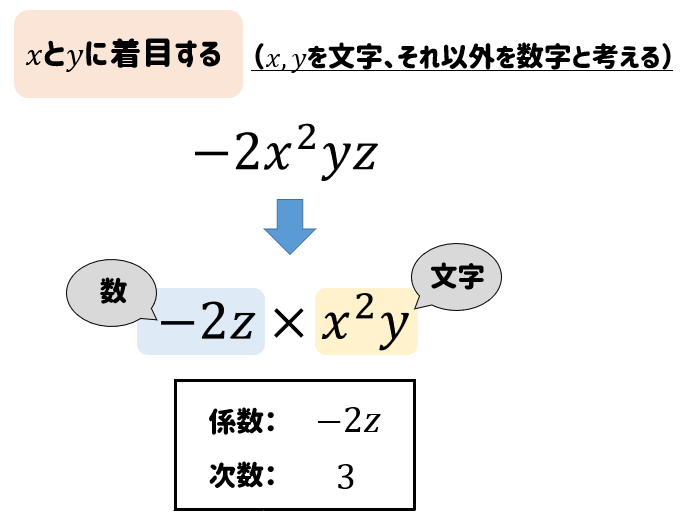
文字が2つになっても考え方は同じですね♪
\(x,y\)を文字と考えているので、文字の個数は3。
それ以外を数と考えているので、\(-3z\)が係数となります。
とにかく!
文字に着目するときのポイントは
着目する文字以外は数と考えるってことですね。
何次式?定数項は?(多項式)
では、次に多項式の場合を考えてみましょう。
次のような問題がよく出題されます。
\(x\)に着目したとき、次の多項式の次数と定数項をいえ。
$$2x^3-2x^2y^2+3x+y-1$$
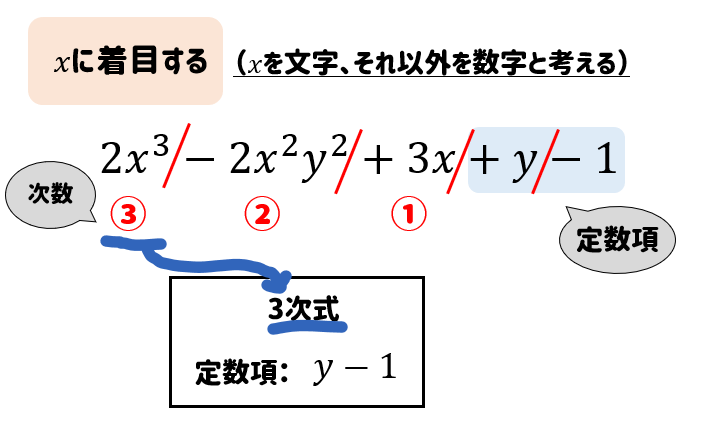
多項式のときには、それぞれの項にわけて次数を調べます。
その中から一番大きい値をその多項式の次数とします。
今回は\(x\)に着目しているので、それぞれの項において\(x\)の個数を調べていけばいいですね。
また、着目している文字を含まない項のことを定数項といいます。
これも新しい用語かもしれませんね。しっかりと覚えておきましょう。
では、もう1問ほど例題を見ておきましょう。
\(x\)と\(y\)に着目したとき、次の多項式の次数と定数項をいえ。
$$3x^2+4xy+2xy^3+x-z$$
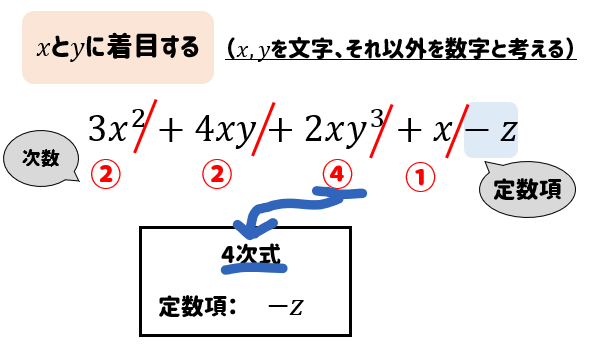
まとめ!
では、文字に着目するときの次数、係数、定数項についてまとめておきましょう。
文字に着目するとは、その文字以外を数として考えるということ。
次数は、着目した文字の個数。
多項式のときには、各項の次数の中から一番大きい数をその多項式の次数とします。
そして、着目した文字を含まない項のことを定数項といいます。
新しい用語が出てきて覚えるのが大変かもしれませんが、考え方はとてもシンプルですね。
今回学んだことは理解を深めるためにも、ぜひ学校のテキストなどを使って演習問題に挑戦してみてください。
では、以上!
今回の記事内容が理解できたら次は降べきの順に挑戦しよう。
⇒ 降べきの順のやり方をイチから!同じ次数や定数項はかっこでくくるようにしよう


















突然で、申し訳ありません。
中学3年生で、高等学校の予習をしている者ですが、質問です。最後の例題の答えで、定数項が、「z」となっていますが、「-z」ではないのですか?未熟者なので、理由をご教授して下さると助かります。
ごめんなさい!
「-z」であってます。
記事が間違っていたので訂正しておきましたm(__)m
高校の予習がんばってください!