こんにちは!数スタの小田です。
今回は中2で学習する『一次関数』の単元から
グラフから式を求める方法について解説していきます。
グラフの書き方をマスターしている人にとっては
すっごく簡単な問題なので、サクッと学習していきましょう。
グラフの書き方についても、事前に学習しておいてくださいね。
では、いきましょー!!
今回の記事は、こちらの動画でも解説しています(/・ω・)/


グラフから式を求める手順
グラフから式を求めるための手順は以下の通りです。
- 切片を読み取る
- 傾きを読み取る
- 式に当てはめる
それでは、それぞれの手順を例題を使って解説していきます。
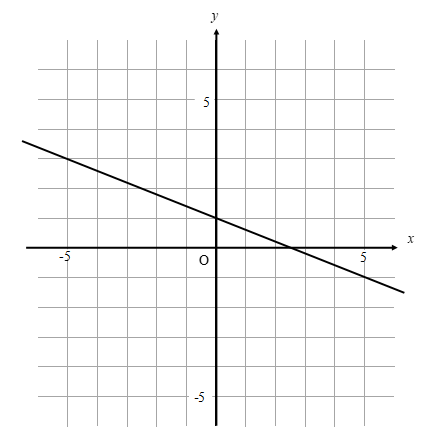
例題
次の直線の式を求めなさい。
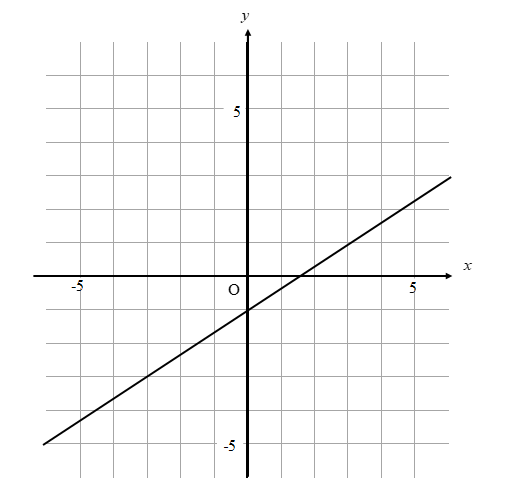

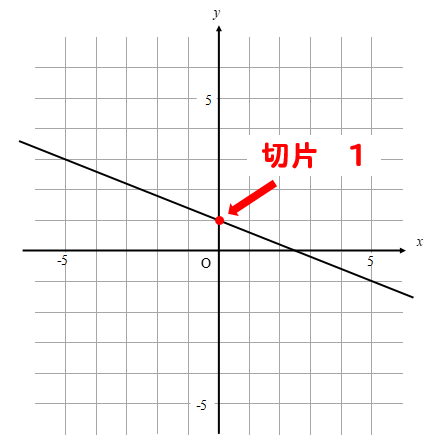
手順① 切片を読み取る
切片とは、y軸と交わる部分のことでしたね。
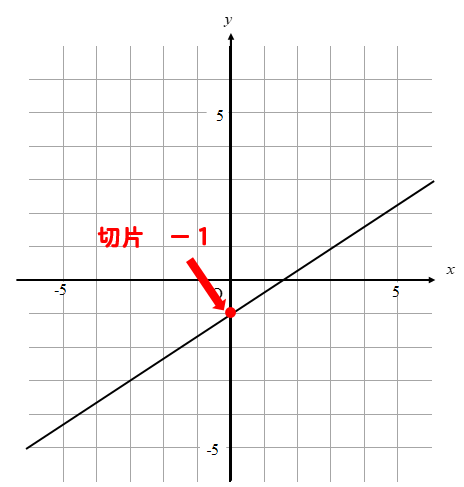

切片は-1になるということが読み取れます。
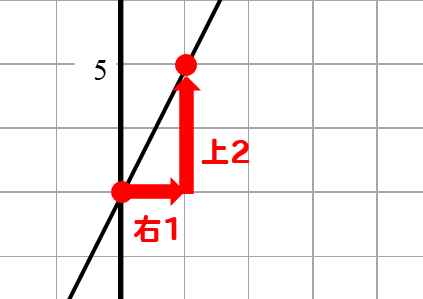
手順② 傾きを読み取る
次はグラフから傾きを読み取ります。
先ほど見つけた切片の場所から
グラフを右にたどっていき
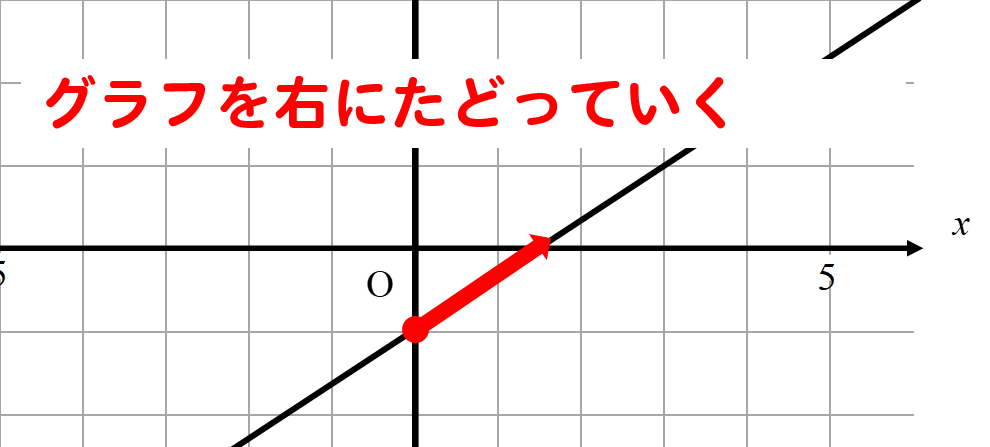

ちょうどぴったり目盛り上を通っているところを見つけます。
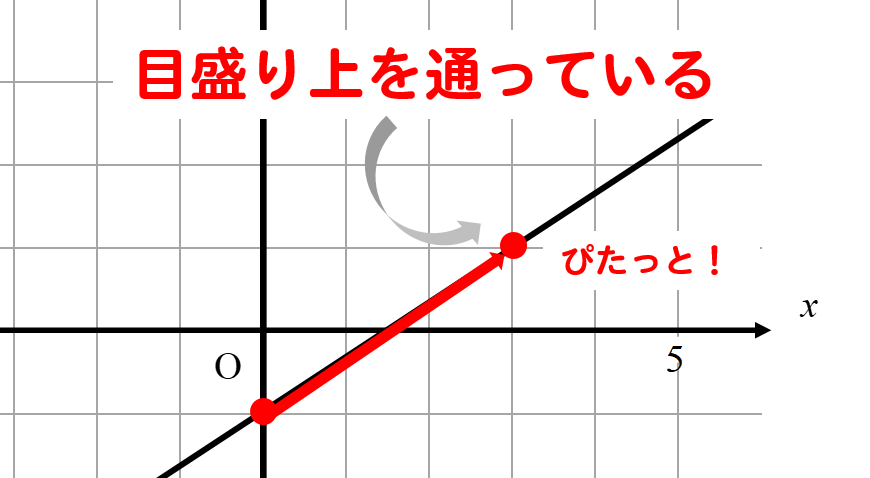

ぴたっとが見つかったら
切片からぴたっとまで
どれくらい移動したかを見ます。
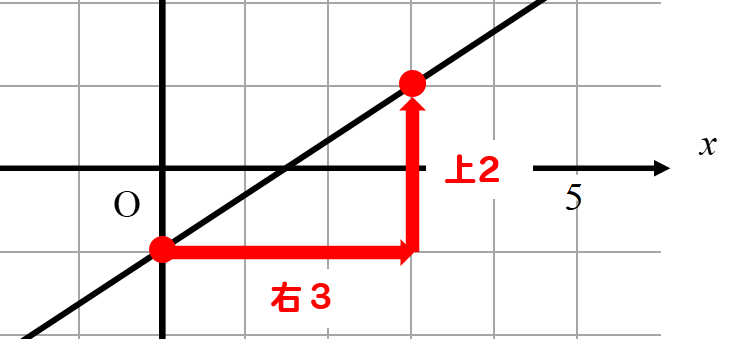

右に3、上に2移動したことが読み取れますね。
傾きは


このように求めることができるので
右に3、上に2を当てはめてみると
傾きは\(\frac{2}{3}\)となります。
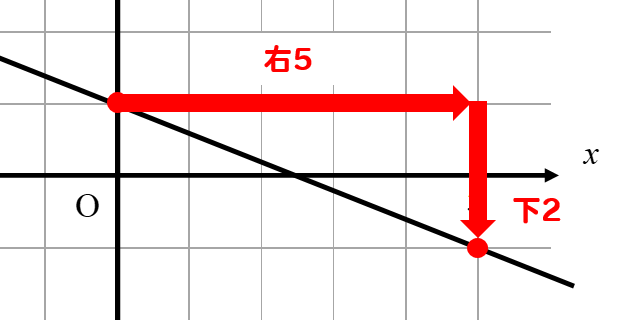
もしも
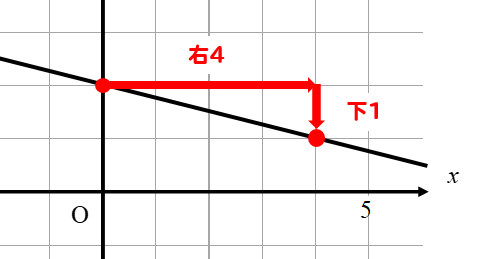

このように右に4、下に-1という状況であれば
傾きは\(-\frac{1}{4}\)となります。
下がっているグラフであれば、マイナスをつけるのを忘れないようにね。
手順③ 式に当てはめる
傾きと切片を読み取ることができれば


一次関数の式に当てはめていけば完成です。
傾き:\(\frac{2}{3}\)
切片:-1
を式に当てはめて
グラフの式は\(y=\frac{2}{3}x-1\)と求めることができました。
このようにグラフから切片と傾きを読み取ることができれば
式を作ることは、とっても簡単です!


それでは、いくつか練習問題を通して理解を深めていきましょう。
演習問題で理解を深める!
次のグラフの式を求めなさい。
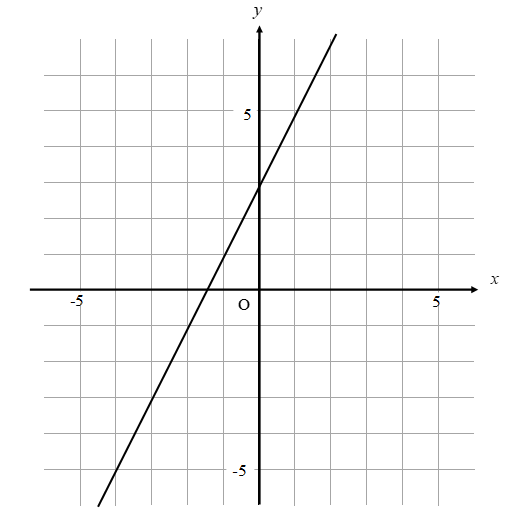
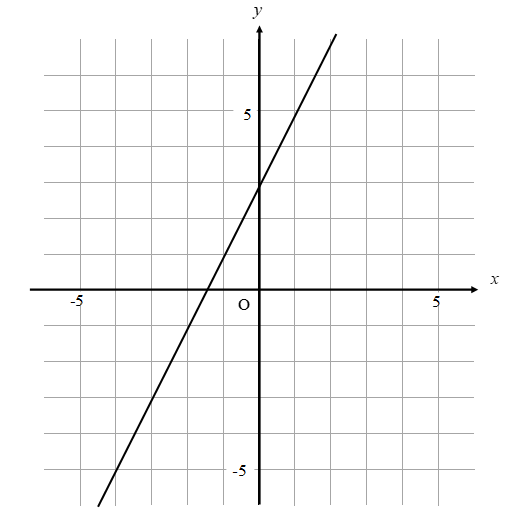
次のグラフの式を求めなさい。



【追加】応用力UPの演習にチャレンジしてみませんか?
お疲れ様でした!
練習問題はバッチリでしたか??
「完璧でしたよ~!!」という方に向けて、
テストで高得点を狙う上でチャレンジしてもらいたい
ちょっと難易度が高い問題を用意してみました(‘ω’)ノ
それがこちらだ!
次のグラフの式を求めなさい。
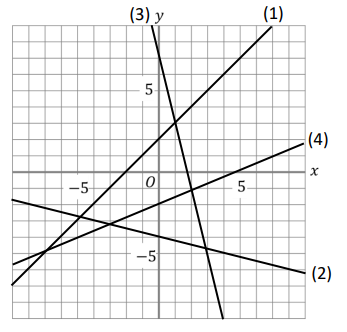



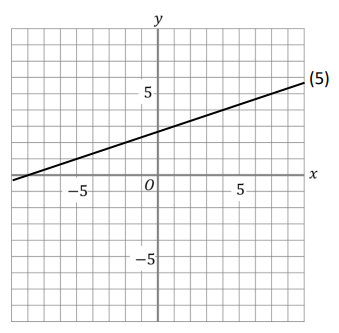

(1)~(4)はまぁ、サクッと解いて欲しい復習問題なんですが、(5)については切片が読み取れない…!ってことで困ってしまいますね(^^;)
必須問題ではありませんが、
テストで80点以上のハイレベルを目指していく方はできるようにしておきたい1問です。
というわけで、ぜひチャレンジしてみてください(‘ω’)ノ
追加演習やってみたよ~!!
という方には、こちらから詳しい解説動画&プリントをお渡ししています。
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
答えが合っているかどうかだけでなく、動画解説を活用して『解法のポイント』『情報の読み取り方』といったところもチェックしておいてくださいね^^
解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに^^
グラフから式を求める方法 まとめ
最後にもう一度、グラフから式を求める手順を確認しておきましょう。
- 切片を読み取る
y軸と交わるところを見て、切片を読み取ります。


- 傾きを読み取る
切片の場所からグラフを右へたどっていき
目盛り上を通っている点を見つけます。


点が見つかれば、どれだけ動いているかを読み取って
傾きの値を求めます。




- 傾きと切片を式に当てはめる
傾きと切片がそれぞれ求めることができたら
一次関数の式に当てはめて完成です!


やり方がわかれば
たくさん練習して問題に慣れていくことが大切です。
さぁ、反復練習だー!
ファイトーーーー(/・ω・)/
一次関数のグラフから式を求める方法を解説!←今回の記事
一次関数の座標の求め方は?いろんな座標を求める問題について解説!

















とってもわかりやすかったっです!
テスト前で焦ってたのですが、これで完璧に求められるようになりました。
テストでグラフの式を求めるものは絶対満点取ってやります( ´∀`)bグッ!
よし、その意気だ!
絶対に満点とってやろう!
これのおかげで、塾の志望校判断テストで数学23点も伸びました!感謝です!
すごいですね!
おめでとうございます^^
引き続き、もっともっと伸ばしていきましょう!
授業の数倍わかりやすくて本当に助かりました!
これで問題集とのにらめっこが減ります!
お役に立てて嬉しいです^^
傾きと切方の違いやマイナスなのかプラスなのかがわかりとくスピードが速くなりました!
もうすぐで実力テストがあるので頑張ります
さすがです!
テストがんばってください^^