【方程式】分母にxがあるときの解き方は？

なんじゃこりゃ！？

$$\large{\frac{1}{x}=2}$$

$$\large{\frac{x}{x+2}=5}$$

$$\large{\frac{1}{x}=x}$$

$$\large{\frac{1}{x}+x=2}$$

分母に\(x\)があるから困ってしまうぞ…

 

今回は、そんな場合の解き方について解説していきます。

理科の濃度計算などでよく出てくる方程式ですね。

 

今回の記事はこちらの動画でも解説しています(^^)

分母にxの解き方！

分数の方程式は、とにかく…

分母をはらう！

というのがポイントとなります。

 

それは分母に\(x\)があっても同じこと

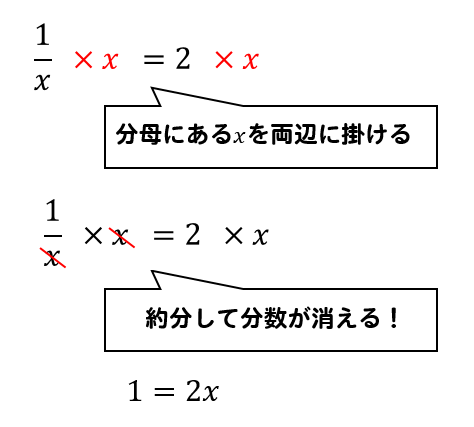
こうすることによって、方程式を普通の形に変形することができます！

 

 

それでは、このやり方で方程式を解いていきましょう。

両辺に\(x\)を掛けると

$$\large{\frac{1}{x}\times x=2\times x}$$

$$\large{1=2x}$$

$$\large{x=\frac{1}{2}}$$

 

両辺に\((x+2)\)を掛けると

$$\large{\frac{x}{x+2}\times (x+2)=5\times (x+2)}$$

$$\large{x=5x+10}$$

$$\large{x-5x=10}$$

$$\large{-4x=10}$$

$$\large{x=-\frac{5}{2}}$$

 

両辺に\(x\)を掛けると

$$\large{\frac{1}{x}\times x=x\times x}$$

$$\large{1=x^2}$$

$$\large{x=\pm 1}$$

 

両辺に\(x\)を掛けると

$$\large{\left( \frac{1}{x}+x\right) \times x=2\times x}$$

$$\large{1+x^2=2x}$$

$$\large{x^2-2x+1=0}$$

$$\large{(x-1)^2=0}$$

$$\large{x=1}$$

 

まとめ

とにかく分母をはらう！

これが大事ですね。

高校数学になると、このような計算をする場面が増えてきます。

分母に\(x\)が出てきても慌てることなく対応していきましょうね(^^)

高校入試で使える公式集をプレゼント！

 
高校入試で使える公式をまとめた教材を作成しました！
 
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/

これは知らないと損をするかも…！？
 
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
 
こちらから公式集を無料で手に入れちゃってください！

ご登録いただいたメールアドレスに教材を送らせていただきます。
 
 
中学生メルマガ講座では、今回のプレゼントのほか


などのプレゼント企画をやっております。
 
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)