今回は一次方程式の利用問題、その中でも過不足の問題について解説していくよ！
過不足というのは、問題文の中に「余る」「足りない」といった言葉が出てきて、とってもややこしく感じる問題だね。
ややこしく感じるんだけど
しっかりとポイントをおさえておけば簡単に解けるようになるから
今回はそのポイントをしっかりと習得してもらいたい！
方程式の計算について確認しておきたい方は、こちらの記事をご参考ください。
>【中１方程式】一次方程式の解き方をまとめておくよ！基本計算～分数、小数まで
過不足の問題とは
過不足の問題とは具体的にこんな感じの問題だよ
問題
何人かの子どもにりんごを配るのに、1人に2個ずつ配ると5個余り、3個ずつ配ると10個足りない。子どもの人数とりんごの個数を求めなさい。
余る？足りない？
何だか、数学よりも日本語が難しく感じる問題だね(;^_^A
過不足の問題でのポイントは
1人に2個ずつ配って5個余るとき
1人に3個ずつ配って10個足りないとき
それぞれのシチュエーションにおいて
配り方は違えど、りんごの個数は同じということ。
つまり
1人に2個ずつ配って5個余るときのりんごの個数
1人に3個ずつ配って10個足りないときのりんごの個数
それぞれを文字で表してやると
個数は同じ値になるので、イコールでつなげてやることができます。
そうすれば方程式は完成です。
個数の表し方は？
方程式の作り方はわかりましたね。
では、りんごの個数を文字で表すにはどうすればよいかを考えてみましょう。
いきなり文字で考えてしまうのは難しいので、簡単な数字で置き換えてみましょう。
例えば
いくつかのりんごを、3人の子どもに2個ずつ配ると5個余る。
こういう状況であれば、りんごは全部で何個あるでしょうか？
子どもに配ることができたりんごは
（りんご2個ずつ）×（子どもの人数）
２×３ ＝ 6個
と表すことができますね。
そして、余っているりんごが5個なので
りんごの合計は6＋5＝11個と考えることができました。
そして、子どもが何人いるかわからないx人という状況でも考え方は同じです。
x人の子ども1人に2個ずつ配って5個余るときのりんごの個数を考えると
子どもに配ることができたりんごは
（りんご2個ずつ）×（子どもの人数）
2×x ＝ 2x個
と表すことができます。
余ったりんごと合わせてやると
りんごの合計は2x＋5個と表せます。
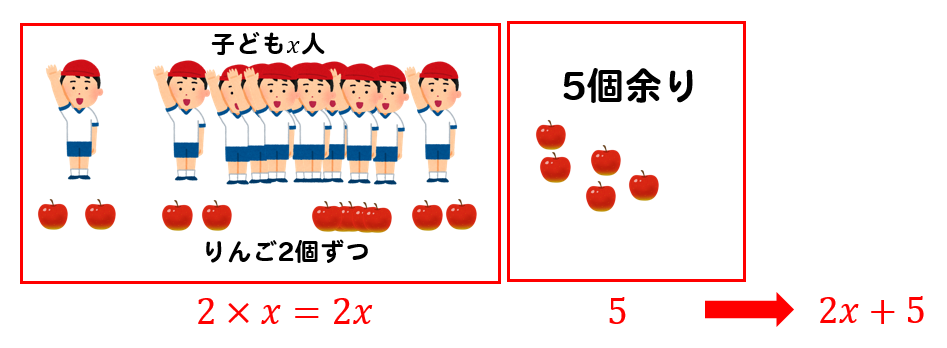
（一人に配る個数）×（人数）＋（余る個数）
次は足りないときの表し方を考えてみましょう。
いくつかのりんごを、4人の子どもに3個ずつ配ると2個足りない。
こういう状況であれば、りんごは何個あるでしょうか。
りんごを3個ずつ4人に配るので、本来なら
（りんご3個ずつ）×（子どもの人数）
３×４ ＝ 12個
子ども全員に3個ずつ配るためには、りんごは12個必要だということになります。
しかし、2個足りなかったということなので
りんごの個数は12－2＝10個ということになりますね。
それでは、これも子どもをx人として文字を用いて考えてみましょう。
x人の子ども1人に3個ずつ配って10個余るときのりんごの個数を考えると
子ども全員に配る3個ずつ配るためには
（りんご3個ずつ）×（子どもの人数）
３×x ＝ 3x個
りんごは3x個必要だということが分かります。
しかし、10個足りないということなので
実際のりんごの個数は3xー10個ということになります。
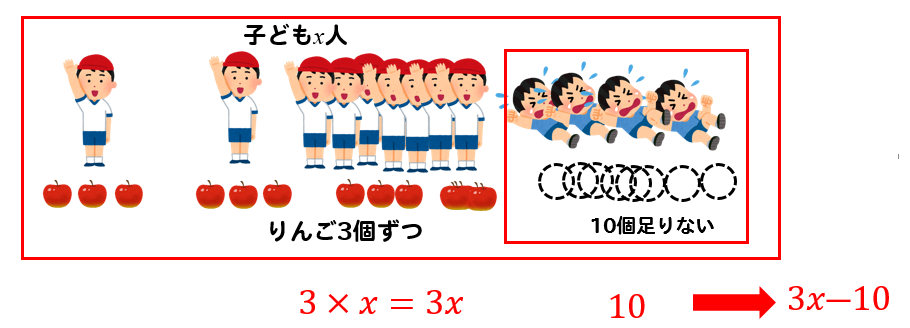
（一人に配る個数）×（人数）ー（足りない個数）
それでは、それぞれを文字であらわす方法を学んだところで先ほどの文章問題を解いてみましょう。
過不足問題の解法
問題
何人かの子どもにりんごを配るのに、1人に2個ずつ配ると5個余り、3個ずつ配ると10個足りない。子どもの人数とりんごの個数を求めなさい。
子どもの人数、りんごの個数
2つの値を問われているので、どちらを文字で置けばいいのか迷ってしまうところなんだけど
初めに言ったように、りんごの個数で方程式を作りたいので人数の方を文字で置いてあげた方が良いです。
ということで
子どもの人数をx人とすると
1人に2個ずつ配ると5個余るということから
りんごの個数は2x＋5と表せます。
3個ずつ配ると10個足りないということから
りんごの個数は3x－10と表せます。
それぞれのりんごの個数は同じはずなので
2x＋5＝3x－10
あとは方程式を計算していきましょう。
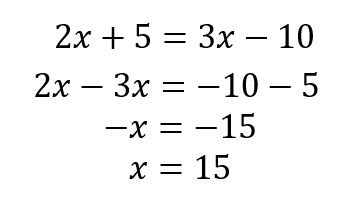
よって、子どもの人数は15人ということがわかりました！
あとは、りんごの個数を求めれば終わりですね。
りんごの個数は文字を使って
2x＋5
3x－10 と表しているので
どちらかの式にx＝15を代入してやればりんごの個数が求まります。
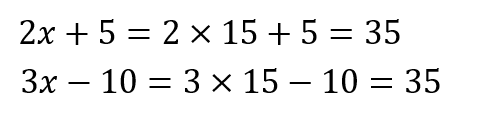
もちろん、どちらに代入しても同じ値が出てくるので、自分が計算しやすそうな方に代入してやるといいですね。
上の式からりんごの個数は35個ということが分かりましたね！
答えは、子ども15人、りんごは35個でした。
練習問題で確認！
それでは、練習問題を通して自分でも式が作れて答えが求められるか確認してみましょう。
何人かの子どもにお菓子を配るのに、1人に3個ずつ配ると15個足りないので、2個ずつ配ると10個余った。子どもの人数とお菓子の個数を求めなさい。
さぁ、挑戦してみてください！
できましたか？
確認してみましょう！
まずは子どもの人数をx人として、お菓子の数をxを用いて表していきます。
1人に3個ずつ配ると15個足りないということで
$$3x-15$$
1人に2個ずつ配ると10個余ったということで
$$2x+10$$
と表すことができました。
それぞれの値は同じになるはずなので
$$3x-15=2x+10$$
あとは計算していきましょう。
$$3x-2x=10+15$$
$$x=25$$
よって、子どもの人数は25人ということが分かりました。
次はお菓子の個数を求めます。
上で表したお菓子の個数の式のどちらかにx＝25を代入して
お菓子の個数は60個だということが分かりました。
答えは、子ども25人、お菓子60個でした。
正解できたかな？
過不足問題のまとめ
それでは、最後に過不足問題のまとめをしておきます。
この問題で大事なのは
配り方は違えど、個数は同じということでしたね。
そこからそれぞれの配り方における個数を文字で表して、イコールで結んであげることで方程式を完成させます。
文字で表すときのポイントは以下の通りでしたね。
余るとき
（一人に配る個数）×（人数）＋（余る個数）
足りないとき
（一人に配る個数）×（人数）ー（足りない個数）
この問題は、計算自体は簡単なので文字の表し方をしっかりと覚えておけば楽勝ですね＾＾
しっかりと練習して身につけていきましょう！
ファイトだー！！
他の文章問題にも挑戦してみましょう。
余る？足りない？過不足の問題を解説！←今回の記事
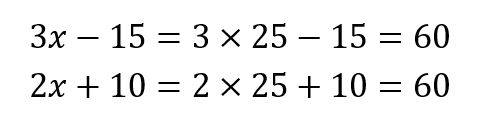
過不足の問題の練習問題で間違い所が思われる所が一つ…
誤 2x+5=3x-10 正 2x+10=3x-15
多分違ってると…
とんでもないミスしてました(^^;
ご連絡ありがとうございました！
すごく分かりやすく簡単に過不足を解けるようになれました！！ありがとうございます！！実はと言うと数学苦手で他のサイトも見ましたが、全く分かりませんでした笑 やっぱこのサイトが1番分かりやすい！！
嬉しいコメントありがとうございます＾＾
過不足はややこしいところなので
しっかりと理解してもらえてよかったです！！
ほんとに分かりやすいです
今日授業でやったんですけど皆分かっているのに自分だけ分からなくてトイレで1人で泣いてました(；＿；)
先生よりずっと分かりやすいです！！ありがとうございます(；＿；)
ありがとうございます＾＾
困ったことがあれば
数スタのサイト、YouTubeを頼りにしてくださいね！
授業で、最近やったんですが…全然分からなくて、
でも、このサイトを見て少しずつわかりました！
すごいわかりやすいかったです！
ここはややこしいところですからね(^^;)
でも、理解してもらえたようで良かったです＾＾
すごくわかりやすくて役に立った‼
テストでもがんばりたい‼
ありがとうございます！
テスト頑張ってくださいね＾＾
とてもわかりやすかったです！
期末テスト前に過不足問題わからなくってそしてこのサイト見たらめちゃくちゃわかりやすくて、期末テストに過不足問題がでて正解することができました！
すばらしい！！