今回は高校数学Ⅱで学習する円の方程式の単元から
『円と直線の交点座標を求める』
について解説していきます。
取り上げる問題はこちら
次の円と直線の交点の座標を求めよ。
$$x^2+y^2=10, y=x+2$$
円と直線の交点を求めるためには？
＞【放物線と直線】交点の座標の求め方とは？解き方を問題解説！
こちらでも解説をしておりますが
とにかく！
交点の座標を求めたかったら
連立方程式を解くべし！
ですね。
円と直線の式を連立方程式で解いてやることによって交点の座標を求めることができます。
それでは、今回の問題を解いていきましょう。
次の円と直線の交点の座標を求めよ。
$$x^2+y^2=10, y=x+2$$
代入法で解いていきます。
\(y=x+2\)を\(x^2+y^2=10\)に代入します。
$$x^2+(x+2)^2=10$$
$$x^2+x^2+4x+4=10$$
$$2x^2+4x-6=0$$
$$x^2+2x-3=0$$
$$(x+3)(x-1)=0$$
$$x=-3,1$$
これで交点の\(x\)座標が求まりました。
次は、\(y\)座標を求めます。
\(x=-3\)のとき、\(y=x+2\)に代入すると
$$y=-3+2=1$$
\(x=1\)のとき、\(y=x+2\)に代入すると
$$y=1+2=3$$
よって、求めたい交点の座標は\((-3,-1)\)、\((1,3)\)となりました。
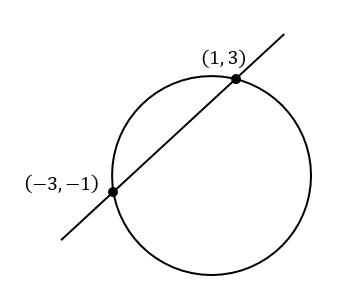
このように、直線を円の式に代入して解いていくことで交点の座標を求めることができます(^^)
それでは！
交点の座標を求める方法について理解を深めるため、さまざまなパターンの練習問題に挑戦してみましょう。
交点座標を求める練習問題に挑戦！
次の円と直線の交点の座標を求めよ。
$$x^2+y^2=4, y=-x+2$$
答え
$$(0,2), (2,0)$$
\(y=-x+2\)を\(x^2+y^2=4\)に代入すると
$$x^2+(-x+2)^2=4$$
$$x^2+x^2-4x+4=4$$
$$2x^2-4x=0$$
$$x^2-2x=0$$
$$x(x-2)=0$$
$$x=0, 2$$
\(x=0\)のとき、\(y=0+2=2\)
\(x=2\)のとき、\(y=-2+2=0\)
よって、\((0,2), (2,0)\)
次の円と直線の交点の座標を求めよ。
$$x^2+y^2=5, x-2y=5$$
答え
$$(1,-2)$$
\(x-2y=5\)を\(x=2y+5\)に変形して、\(x^2+y^2=5\)に代入すると
$$(2y+5)^2+y^2=5$$
$$4y^2+20y+25+y^2=5$$
$$5y^2+20y+20=0$$
$$y^2+4y+4=0$$
$$(y+2)^2=0$$
$$y=-2$$
\(y=-2\)のとき、\(x=-4+5=1\)
よって、\((1,-2)\)
交点が1つしかないということは
このように直線と円が接しているということですね。
次の円と直線の交点の座標を求めよ。
$$x^2+y^2=50, x-2y+20=0$$
答え
$$交点なし$$
\(x-2y+20=0\)を\(x=2y-20\)に変形して、\(x^2+y^2=50\)に代入すると
$$(2y-20)^2+y^2=50$$
$$4y^2-80y+400+y^2=50$$
$$5y^2-80y+350=0$$
$$y^2-16y+70=0$$
\(y\)についての二次方程式ができましたが、これを解こうとすると困ってしまいます…
…解けない！！
解の公式を用いても、ルートの中身がマイナスになってしまい困ります。
そこで、この方程式を判別式にかけてやると
$$\frac{D}{4}D=(-8)^2-1\times 70=-6<0$$
負になることから、方程式の解はなし！ということが確かめられました。
方程式の解がないということは、交点の座標もなしということになります。
まとめ
お疲れ様でした！
円と直線の交点座標を求めたい場合には、連立方程式を解きましょう。
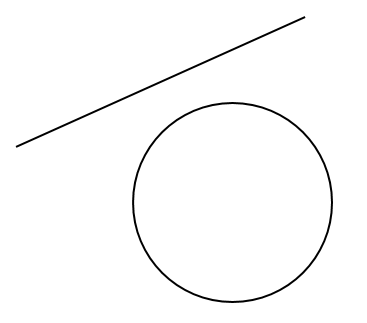
ただし、連立方程式を用いて解が出てこない場合もあります。
そのときには円と直線は交点を持たないということになります。
こういったイレギュラーなパターンもあるから、頭に入れておこうね！
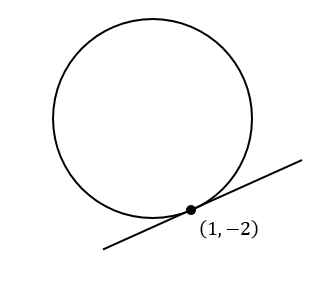
コメントを残す