円の方程式の求め方まとめ！パターン別に解説するよ！

今回は高校数学Ⅱで学習する円の方程式から

『円の方程式の求め方』

について問題解説をしていくよ！

今回取り上げる問題はこちらだ！

今回の内容をサクッと理解した方は、こちらの動画がおススメです！

円の方程式　基本形と一般形

円の方程式を求めるためには、式の形を覚えておく必要があります。

それが次の２つの形です。

(1)(2)基本形の円の方程式

中心と半径が与えられている問題では基本形である

$$(x-a)^2+(y-b)^2=r^2$$

の式に数を当てはめていけばOKです。

中心が原点で、半径2の円ということから

\(a=0,　b=0,　r=2\)を当てはめていくと

$$x^2+y^2=4$$

となります。

中心\((2, 3)\)で、半径5の円ということから

\(a=2,　b=3,　r=5\)を当てはめていくと

$$(x-2)^2+(y-3)^2=25$$

となります。

標準形の式に当てはめていくだけなので、とっても簡単でしたね(^^)

(3)(4)軸に接する円の方程式

今回の問題でも、中心が与えられているので標準形の式を使っていきます。

\(x\)軸、\(y\)軸に接している場合、中心の座標から半径を求めることができる！

というのが問題を解くためのコツとなります。

まず、\(x\)軸と接しているというのは次のような状況です。

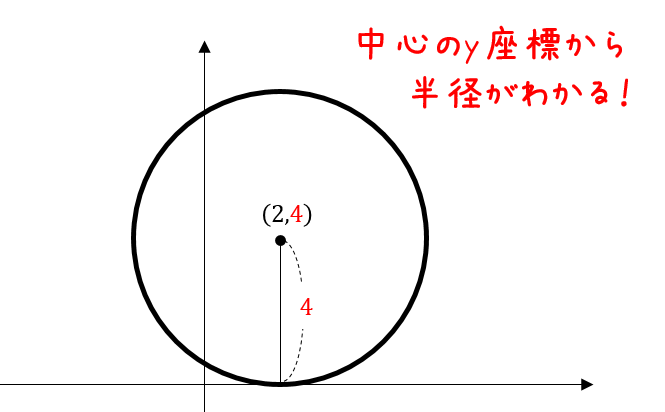
中心の\(y\)座標を見ると、半径の大きさが分かりますね！

\(y\)軸と接しているというのは次のような状況です。

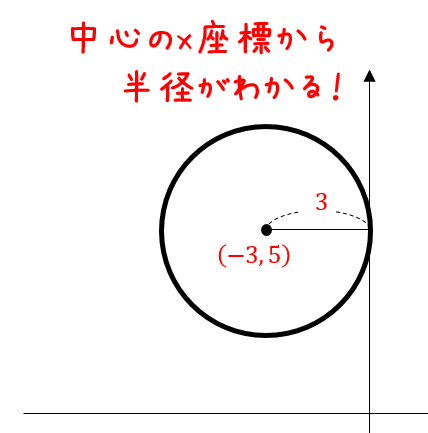
中心の\(x\)座標を見ると、半径の大きさが分かりますね！

符号がマイナスの場合には取っちゃってくださいな。

それでは、このことを踏まえて問題を見ていきます。

中心\((2, 4)\)で、\(x\)軸に接する円ということから

半径が4であることが読み取れます。

よって、\(a=2,　b=4,　r=4\)を当てはめていくと

$$(x-2)^2+(y-4)^2=16$$

となります。

中心\((-3, 5)\)で、\(y\)軸に接する円ということから

半径が3であることが読み取れます。

よって、\(a=-2,　b=5,　r=3\)を当てはめていくと

$$(x+2)^2+(y-5)^2=9$$

となります。

軸に接するときたら、中心の座標から半径を求めよ！

ですね(^^)

\(x\)、\(y\)のどちらの座標を見ればいいか分からない場合には、軸に接しているイメージ図を書いてみると分かりやすいね！

\(x\)、\(y\)軸、両方ともに接する円の方程式についてはこちらの記事で解説しています。

＞x軸、y軸と接する円の方程式を求める方法とは？

(5)中心と点を通る円の方程式

こちらの問題も中心が与えられているので、基本形を使って解いていきます。

中心\((4, -5)\)であることから

$$(x-4)^2+(y+5)^2=r^2$$

ここまで式を作ることができます。

次に、点\((3, 2)\)を通るということから\(x=3,　y=2\)を代入すると

$$(3-4)^2+(2+5)^2=r^2$$

$$1+49=r^2$$

$$r^2=50$$

$$r>0より$$

$$r=5\sqrt{2}$$

このようにして、半径を求めることができました。

以上より

$$(x-4)^2+(y+5)^2=50$$

となります。

また、中心と円が通る座標の距離から半径を求めるということもできます。

それぞれ、自分が好きなやり方で半径を見つけてください(^^)

(6)2点座標、直径から円の方程式

直径となるような2点の座標が与えられた場合、ここから中心と半径を求めていきます。

中心と半径が分かるようになるので、基本形の式を用いていきます。

まず、直径の両端となる座標から中心を求めます。

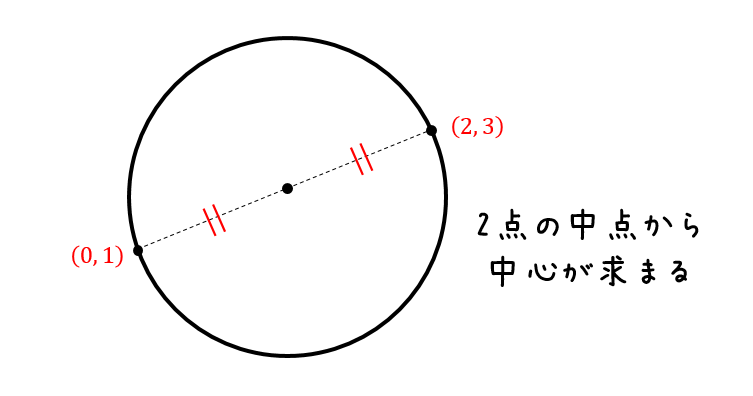
それぞれの中点が中心となるので

$$\left( \frac{0+2}{2},　\frac{1+3}{2}\right)=\left( 1,　2\right)$$

となります。

次は、中心と円が通る座標を用いて半径を求めましょう。

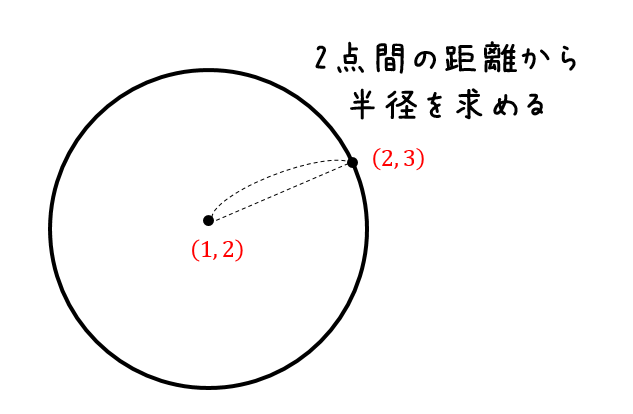
すると、半径の大きさは

$$r=\sqrt{(2-1)^2+(3-2)^2}=\sqrt{2}$$

となります。

以上より、円の方程式は

$$(x-1)^2+(y-2)^2=2$$

となります。

(7)3点から円の方程式

3点の座標を与えられた場合には、円の方程式の一般形を利用していきましょう。

$$x^2+y^2+lx+my+n=0$$

3点の座標をそれぞれ一般形の式に代入して3つの式を作ります。

\((-2,3)\)から

$$4+9-2l+3m+n=0$$

$$-2l+3m+n=-13$$

\((2,-1)\)から

$$4+1+2l-m+n=0$$

$$2l-m+n=-5$$

\((4,1)\)から

$$16+1+4l+m+n=0$$

$$4l+m+n=-17$$

これら3つの式を連立して方程式を解いていきます。

\begin{eqnarray} \left\{ \begin{array}{l} -2l+3m+n=-13 \\ 2l-m+n=-5 \\ 4l+m+n=-17\end{array} \right. \end{eqnarray}

3つの連立方程式を解く方法については

＞【連立方程式】3つの文字、式の問題を計算する方法は？

こちらの記事をご参考ください(^^)

すると、\(l, m, n\)はそれぞれ

$$l=-2,　m=-4,　n=-5$$

となります。

以上より、円の方程式は

$$x^2+y^2-2x-4y-5=0$$

となります。

今回の問題のように3点の座標が与えられた場合には、一般形の式を用いて連立方程式を解いていきましょう。

ちょっと計算がめんどいけど…そこはファイトだぞ！

(8)直線に接する円の方程式

中心が与えられているので、基本形の式を用いて解いていきます。

直線と接する場合

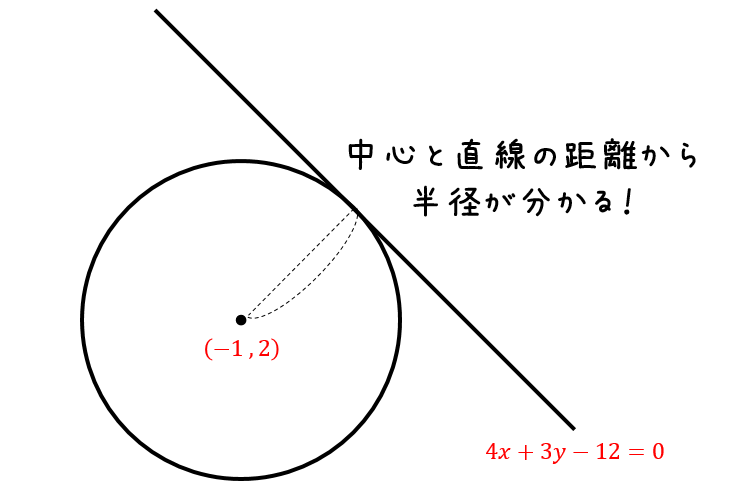
このように、中心と直線との距離を調べることにより半径を求めることができます。

$$r=\frac{|4\times (-1)+3\times 2-12|}{\sqrt{4^2+3^2}}$$

$$=\frac{|-10|}{5}$$

$$=\frac{10}{5}$$

$$=2$$

以上より、円の方程式は

$$(x+1)^2+(y-2)^2=4$$

となります。

直線に接するとくれば、中心と直線の距離から半径を求める！

(9)中心が直線上にある円の方程式

中心について与えられている問題なので基本形の式を利用して解いていきます。

まず、中心が直線\(y=2x\)上にあるということから中心の座標を\((t,　2t)\)と表すことができます。

更に、点\((1,1)\)を通り、\(y\)軸に接するということから、円の中心はこのように第１象限にあるということが読み取れます。

つまり、中心の\(x\)座標である\(t\)は正の値であり、半径は\(t\)であることも分かります。

このことから、中心は\((t,　2t)\)であり半径は\(t\)であることから

$$(x-t)^2+(y-2t)^2=t^2$$

という式が作れます。

そして、この円が点\((1,1)\)を通るということから

$$(1-t)^2+(1-2t)^2=t^2$$

$$1-2t+t^2+1-4t+4t^2=t^2$$

$$4t^2-6t+2=0$$

$$2t^2-3t+1=0$$

$$(2t-1)(t-1)=0$$

$$t=1,　\frac{1}{2}$$

以上より、円の方程式は

$$(x-1)^2+(y-2)^2=1$$

$$\left(x-\frac{1}{2}\right)^2+(y-1)^2=\frac{1}{4}$$

となります。

今回の問題のように、中心が直線上にある場合には文字を使って中心を表すことがポイントとなりますね！

まとめ

お疲れ様でした！

円の方程式を求める場合には基本形と一般形を使い分けることが大切です。

問題文で中心や半径についての与えられた場合には基本形！

$$(x-a)^2+(y-b)^2=r^2$$

$$中心(a, b)、半径 r $$

3点の座標のみ与えられた場合には一般形！

$$x^2+y^2+lx+my+n=0$$

となります。

上でパターン別に問題を紹介しましたが、ほとんどが基本形でしたね。

基本形を使った問題は種類が多いのでたくさん練習しておく必要がありそうです。

ファイトだー(/・ω・)/