今回は中3で学習する
『相似な図形』の単元の中から
入試によく出題されている
平行四辺形と面積比の問題について解説していくよ!
こーーーんな図形の問題です。

なんか見た目が難しそうだよね…

でも、この記事で解説していくことをちゃんと理解してもらえれば大丈夫!
さぁ、がんばっていこー!!
まず知っておきたい面積比のこと
まず、問題に挑戦する前に
面積比について知っておいてもらいたい2つのことがあります。
まず、一つは
- 相似な図形において、面積比は相似比の2乗になる
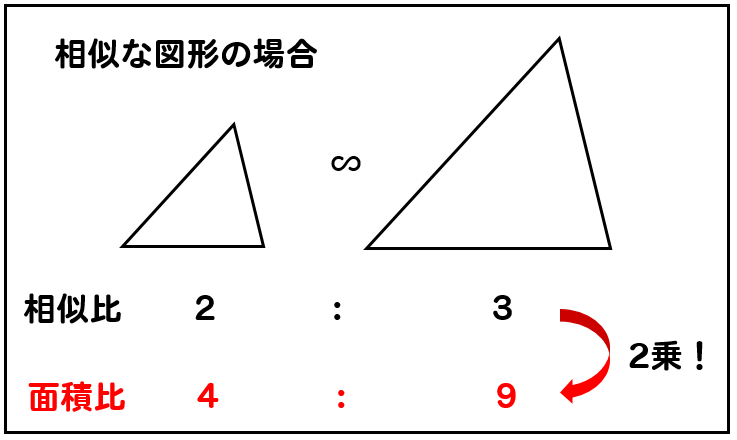
比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。
もう一つは
相似な図形でなくても
- 高さが等しければ、底辺の長さの比が面積比になる

比べる三角形が相似でなくても、高さが等しければ
底辺の長さの比が、そのまま面積比となります。
この2つのことをよく覚えておいてください!
この後、使っていくからねー
問題解説!
問題
下の図の平行四辺形ABCDで、BC上にBE:EC=3:2となる点Eをとり、AEとBDの交点をPとする。
△PBEの面積が18㎠のとき、平行四辺形の面積を求めなさい。

平行四辺形の面積を求めたいのですが
全体を一度に求めようとすると難しいので
平行四辺形の半分に当たる△ABDの面積を求めてやります。
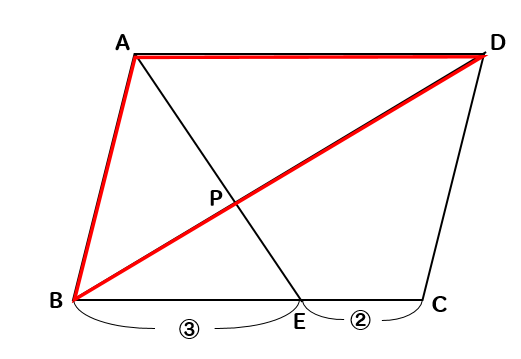
その後、△ABDの面積を2倍してやれば平行四辺形が求められますね。
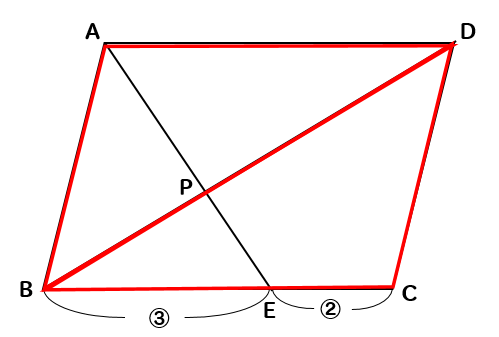
というわけで、△ABDに近づくため
まずは△APDの面積を求めます。
平行四辺形の性質よりAD=BCなので
ADは⑤と考えることができます。
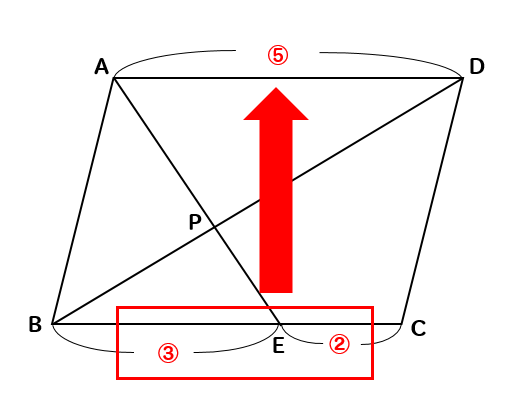
そして、△PBEと△PDAは相似関係にあるので
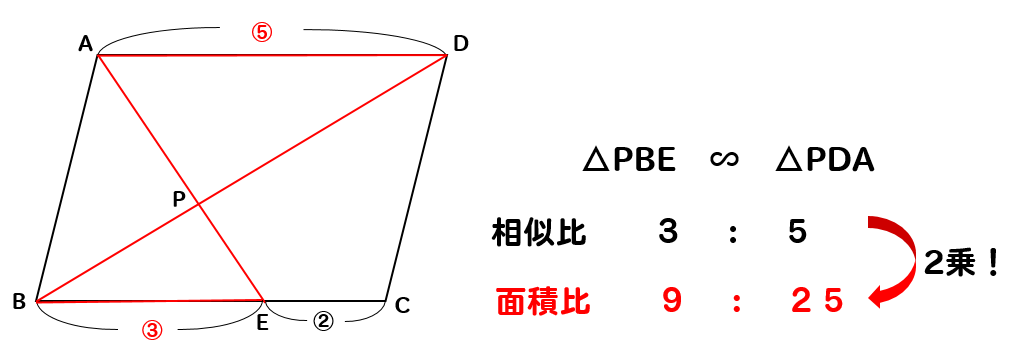
△PBEと△PDAの面積比は9:25とわかります。
ここで、△PBEの面積が18㎠ということから
$$9:25=18:x$$
$$9x=25\times18$$
$$9x=450$$
$$x=50$$
よって、△PDAの面積は50㎠だとわかります。
つぎは△ABPの面積を求めるために
△ABDに着目します。
△PBE∽△PDAより
$$PB:PD=3:5$$
ということがわかります。
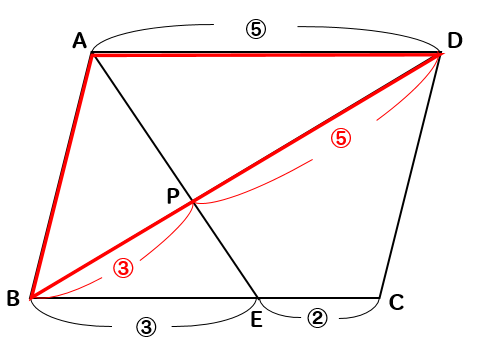
次に△ABDを△ABPと△ADPに分けて考えると
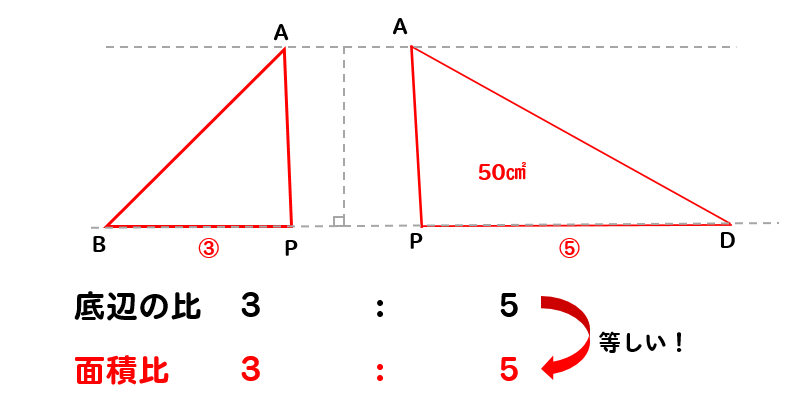
2つの三角形は同じ高さになっているので
底辺の長さの比3:5がそのまま面積比となります。
よって、△ABPの面積は
$$3:5=x:50$$
$$5x=3\times50$$
$$5x=150$$
$$x=30$$
よって、△ABPの面積は30㎠とわかります。
これで△APD、△ABPの面積が求まったので
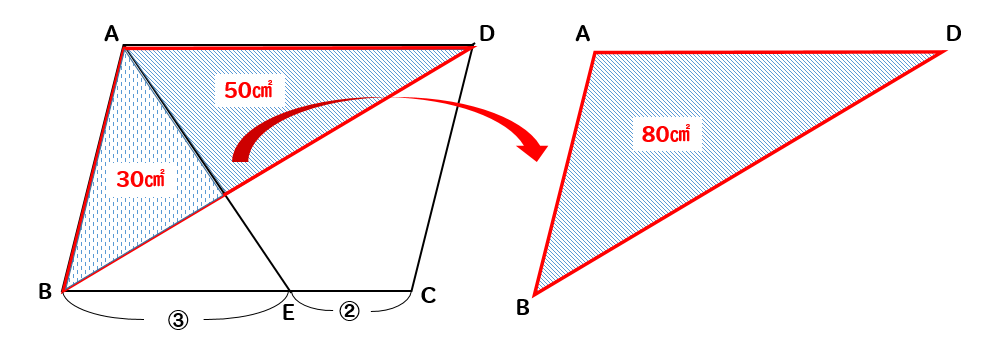
△ABDの面積は80㎠となります。
よって、求めたい平行四辺形の面積は
△ABDを2倍したものになるので
答えは160㎠となります。
このように、平行四辺形の中にある三角形を見つけながら
相似な図形から面積比を求めたり
高さが等しい三角形から面積比を求めたりします。
それでは、ちょっと発展した問題にも挑戦してみましょう!

問題解説(発展)!
問題
下の図の平行四辺形ABCDで、BCを3等分する点をBに近い方からP、Qとする。また、AQとDPの交点をRとするとき、平行四辺形ABCDの面積は△RPQの何倍になるか求めなさい。
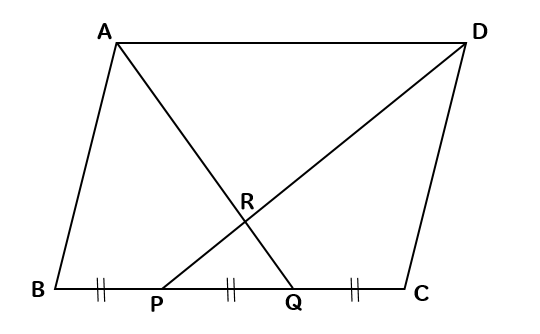
考え方としては
△RPQの面積を1として
平行四辺形ABCDの面積を求める。
それでは、先ほど考えた問題と同じように
相似な図形や、高さが等しい三角形に注目して面積比を求めていきましょう。
まずは
$$BP:PQ:QC=1:1:1$$
より
ADは③と考えることができます。
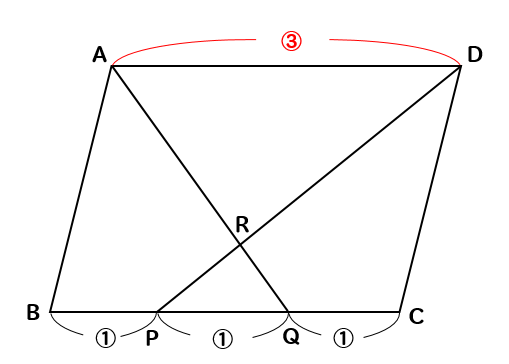
すると、△RPQと△RDAは相似な三角形なので
$$RP:RD=1:3$$
ということがわかります。
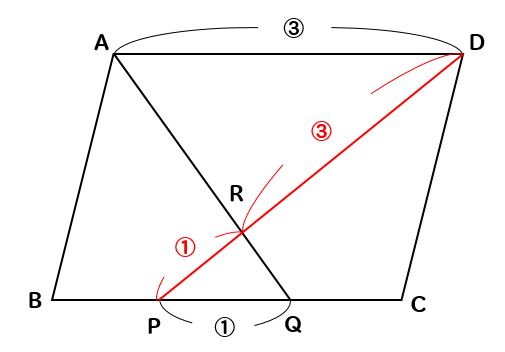
次はDQに補助線を入れて、△PQDに着目します。
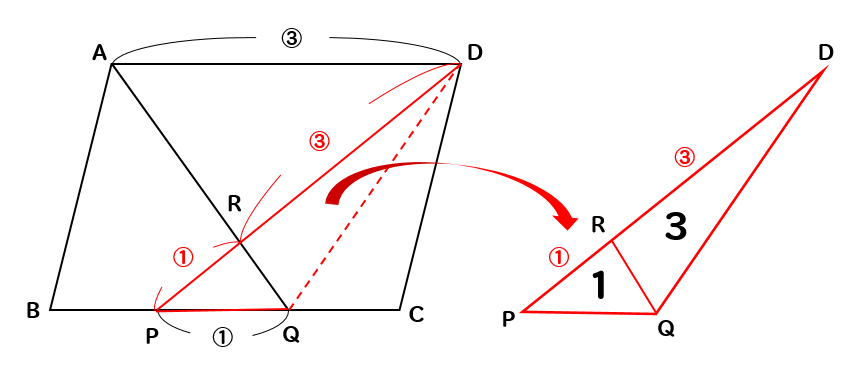
すると、△RPQと△RDQは高さが等しい三角形なので
底辺の長さの比が面積比となります。
よって、面積比は1:3なので
△RDQの面積は3
△PQDの面積は4とわかります。
次に
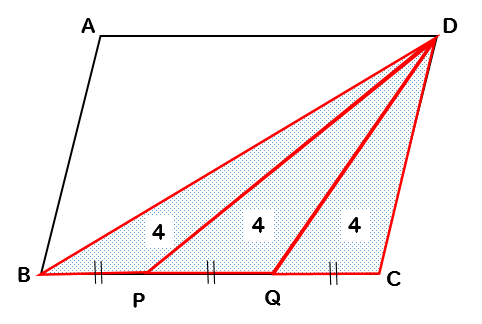
このように△BPD、△PQD、△QCDは高さが等しい三角形なので
底辺の長さの比が面積比となります。
すべて底辺の長さは等しいので
面積も全て等しくなり、面積はそれぞれ4ということがわかります。
よって、△DBCの面積は12
平行四辺形の面積は△DBCを2倍した値になるので24となります。
以上より
△RPQの面積を1としたとき、平行四辺形ABCDの面積は24となるので
答えは24倍となります。
ちょっと難しかったけど
これも面積比を確実に見ていけば大丈夫な問題ですね!
まとめ
平行四辺形の面積比に関する問題は以下の2つをしっかりと覚えておきましょう。


はじめの頃は
どこの三角形に注目すればいいんだろう…と悩むことも多いですが
慣れてくると
自然と注目する三角形が浮き上がって見えてくるようになります。
そうなるためには
問題演習あるのみです!
学校のワークや参考書を使って、ひたすら練習だ!
ファイトだー(/・ω・)/
台形の面積比問題の解説はこちらをどうぞ!
面積比!平行四辺形の面積問題を解説!←今回の記事


















コメントを残す