【算数】分数を通分するときの最小公倍数を簡単に見つける方法を解説！

今回学習していくのは

分数の通分について！

分数の足し算、引き算が苦手な人の特徴として

やっぱり通分ができていない。

逆に言えば、通分さえしっかりとできるようになれば分数の計算はバッチリ！

という訳で、今回は分数の通分について深堀りしていこう！

分母の最小公倍数に揃える

$$\LARGE{\frac{1}{2}+\frac{1}{3}}$$

分数の足し算、引き算において、分母の数が違う場合

$$\LARGE{\frac{1}{2}+\frac{1}{3}}$$

$$\LARGE{=\frac{3}{6}+\frac{2}{6}}$$

$$\LARGE{=\frac{5}{6}}$$

このように、それぞれの分母にある数の最小公倍数に通分することで計算を進めていきます。

そして、通分の作業において一番苦労するのが

最小公倍数を見つけるという作業なんですよね。

これが瞬時に見つけれるようになると分数の計算も楽になってきます。

という訳で、次では最小公倍数を簡単に見つけていくテクニックについてお話を進めていきます。

と、その前に

あれ…最小公倍数ってなんだっけ？

という方もおられますよね。

ちょっとだけ復習しておきましょう。

最小公倍数ってなんだっけ？？

まず、倍数という言葉を確認しておきましょう。

倍数とは、その数に整数を掛けて出来上がる数のことを言います。

言葉で説明すると難しく感じますね(^^;

例えば

2の倍数であれば

$$2\times 1=2$$

$$2\times 2=4$$

$$2\times 3=6$$

$$2\times 4=8$$

$$2\times 5=10$$

このように、２に整数を掛けてできあがる数のことが2の倍数です。

まぁ、小学生の方には九九で2の段に出てくる数だよね～！っていうとしっくりくるかな。

次に公倍数という言葉を確認しておきましょう。

公倍数とは、共通する倍数のことを言います。

例えば、２と３の公倍数を考えると

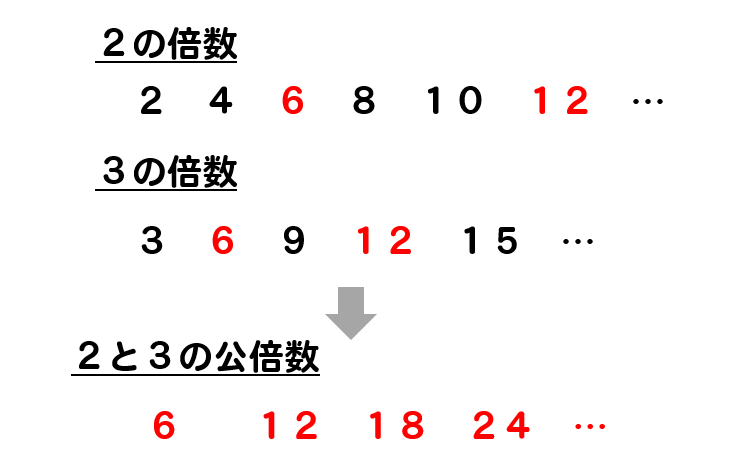
このように、2の倍数と3の倍数の中から共通する数を見つけてくればコレが公倍数となります。

更に、公倍数の中で最も小さい数を最小公倍数と言います。

つまり、２と３の最小公倍数は６ということになります。

最小公倍数の意味はOKかな？

次では、最小公倍数を簡単に見つける方法について学習していこう！

最小公倍数を簡単に見つける方法

通称「逆わり算」というものを使います。

某小学校では、そういう名称で呼ばれておりましたのでこの記事でも逆わり算と呼ばせてもらいます。

例えば、６と９の最小公倍数を見つけたいとき

まずは、このように６と９を書いて筆算をするときに使う割り算のマークを逆にして書きます。

そして、両方の数を割ることができる数を見つけて割っていきます。

約分をするのと同じ感覚ですね。

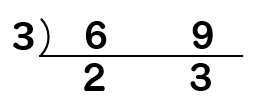
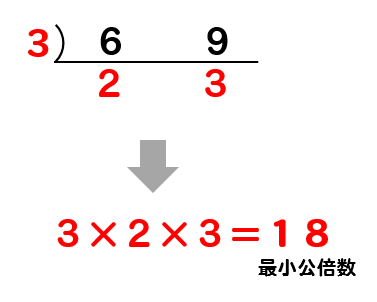
６と９はそれぞれ３で割れるので、３で逆わり算をしてやると２と３が出てきます。

２と３はこれ以上、割ることができませんね。

このように、これ以上割ることできなくなるまで逆わり算を続けていきます。

これ以上、割れなくなったら今まで割ってきた数と残った数を全て掛け合わせると、それぞれの数の最小公倍数を見つけることができます。

もう少し大きい数で練習してみましょうか。

３６と４８の最小公倍数を逆わり算を使って求めてみましょう。

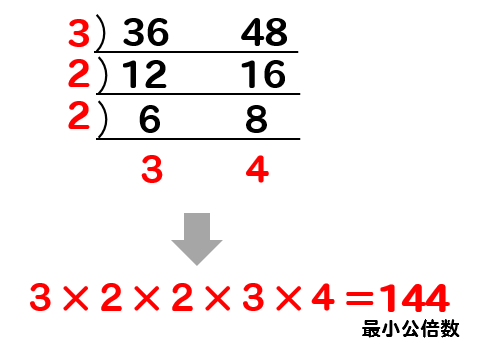
このように最小公倍数が144になることがすぐに求まりました！

大きな数であればあるほど、逆わり算という方法は役に立ちますね(^^)

なぜ逆わり算で最小公倍数が求まるのか

では、なぜこのような方法で最小公倍数が求まるのかについて簡単に触れておきますね。

これは高校生になると深く学習するようになるので、小学生の内はなんとなくのイメージを持っておいてもらえるだけでも十分かと思います。

実は、逆わり算をすることでそれぞれの数をパーツに分解したことになります。

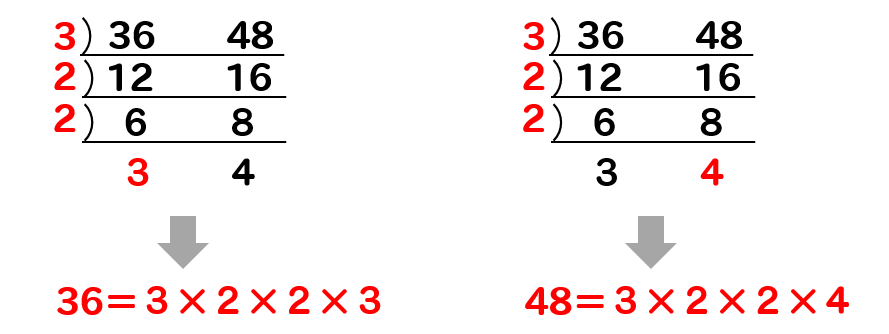
つまり

３６という数は２が２つ、３が２つのパーツでできている。

４８という数は２が２つ、３が１つ、４が１つのパーツでできている。

ということが逆わり算をすることによって分かります。

そして、最小公倍数である１４４のパーツを見てもらうと分かる通り

それぞれのパーツの共通部分と、オリジナルパーツを組み合わせて出来上がった数になっています。

逆わり算の形で確認するとこんな感じですね。

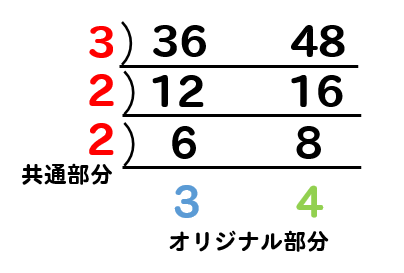
逆わり算の計算をすることで、それぞれの共通パーツとオリジナルパーツを瞬時に見分けることができるんですね。

あとは、これらのパーツを掛け合わせるだけで最小公倍数の完成となるわけです。

なんか、上手く説明できた気がしませんが(^^;

数はパーツ分けすることができて

最小公倍数とは、それぞれの共通パーツとオリジナルパーツを組み合わせることで作り上げることができる。

そして、それぞれのパーツを見つけるためには逆わり算という方法が便利なんだ！ということですね。

3つの場合はどうする？

さて、ちょっと応用編に突入します。

３つの数の最小公倍数を見つけるときにはどうしたらよいでしょうか。

２つのときと同じように逆わり算を使って求めていくのですが、少しだけ注意する点があります。

例えば

２４と９０と１８０の最小公倍数を見つけたいとき

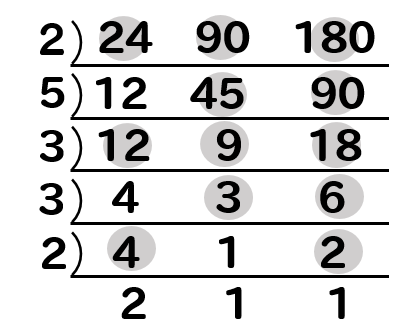
このように逆わり算をやっていくのですが

割るときには、３つの数を全て割らなくてもOKです。

３つの内２つでも割ることができれば、どんどん割って計算を進めていきます。

割れなかったところは、そのままの数にしておいて次の計算に進んでいきます。

よって、それぞれのパーツが分かったので

以上より最小公倍数は360だということが分かりました！

分数の計算で実践してみよう！

それでは、最小公倍数の見つけ方が分かったところで、分数の計算で実践してみましょう。

まずは、逆わり算を使って２４と３６の最小公倍数を見つけましょう。

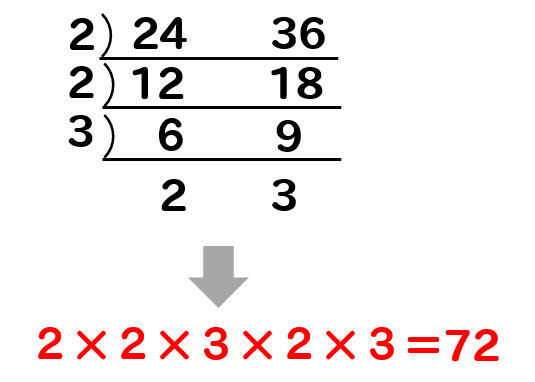
ちなみにそれぞれのパーツを見れば

何倍すれば最小公倍数になるのかも分かっちゃうから便利だよね。

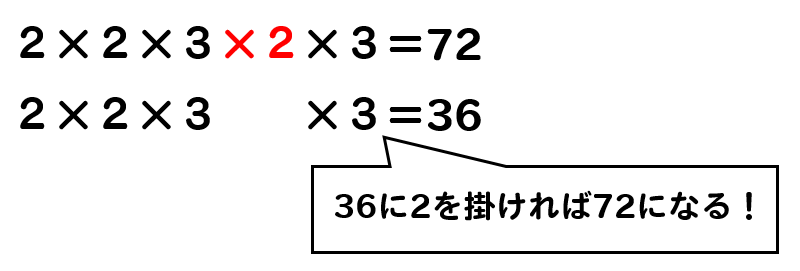
それでは、それぞれの数に何を掛ければ最小公倍数になるのかも分かったところで通分して計算していきましょう。

$$\Large{\frac{1}{24}+\frac{1}{36}}$$

$$\Large{=\frac{3}{72}+\frac{2}{72}}$$

$$\Large{=\frac{5}{72}}$$

完成！

通分を乗り切れば、計算自体は簡単だね(^^)！

まとめ

お疲れ様でした！

最小公倍数の求め方はこれでバッチリですね！

知っておいて損はない方法だと思います。

小学校によっては、算数に力を入れている先生が授業の中で教えてくれることもあるようですが、稀なケースのようです。

知っている人だけ得するなんてズルいｗ

だから、この記事を通してたくさんの方が通分を得意になってくれると嬉しいです(^^)