今回の記事では、数学Ⅰで学習する三角比の単元から
次の2パターンの問題について解説していきます。
【問題①】
木がある場所から水平に20m離れた地点で、気の先端を見上げたところ、水平面とのなす角が40°であった。木の高さを求めよ。ただし、\(\tan40°=0.8391\)とし、小数第2位を四捨五入せよ。
【問題②】
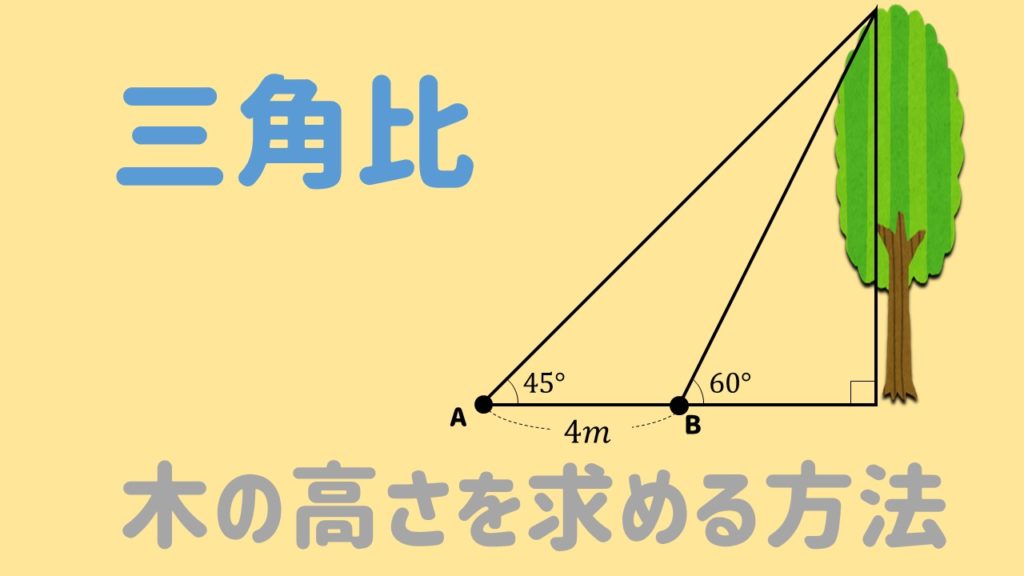
ある地点Aから木の先端Pの仰角は45°、木に向かって水平に4m進んだ地点BからPの仰角は60°だった。木の高さを求めよ。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
三角比を使って木の高さを求める
三角比を使って高さ、水平の距離などを調べるときには次の式を覚えておきたい!
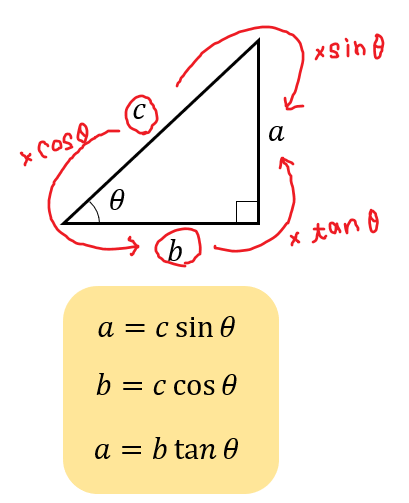
問題①の解き方と考え方
【問題①】
木がある場所から水平に20m離れた地点で、気の先端を見上げたところ、水平面とのなす角が40°であった。木の高さを求めよ。ただし、\(\tan40°=0.8391\)とし、小数第2位を四捨五入せよ。
文章だけではイメージがしずらいので、まずは図を書いてみましょう。
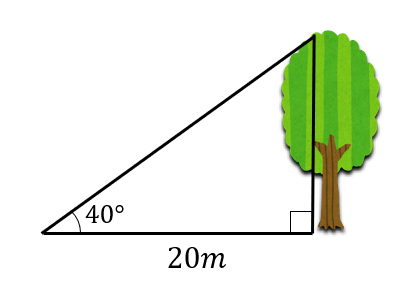
すると、このように直角三角形を作ることができました。
つまり、木の高さは直角三角形の高さを求めればよいということになります。
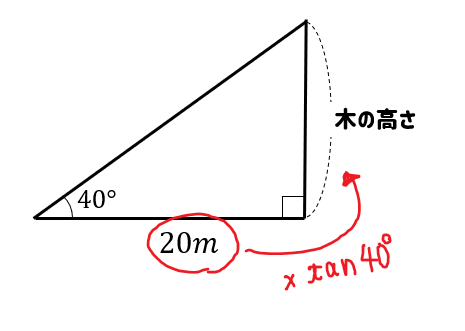
底辺にあたる20に\(\tan40°\)をかければよいので
$$\begin{eqnarray}(木の高さ)&=&20\times \tan40°\\[5pt]&=&20\times 0.8391\\[5pt]&=&16,782 \end{eqnarray}$$
小数第2位で四捨五入すると、木の高さは16.8mとなります。
水平方向の距離がわかっていれば、それに\(\tan\)をかければ高さが求まります。
問題②の解き方と考え方
【問題②】
ある地点Aから木の先端Pの仰角は45°、木に向かって水平に4m進んだ地点BからPの仰角は60°だった。木の高さを求めよ。
仰角(ぎょうかく)という聞きなれない言葉がありますが、これは水平面とのなす角のことです。
つまり、見上げたときの角度ですね。
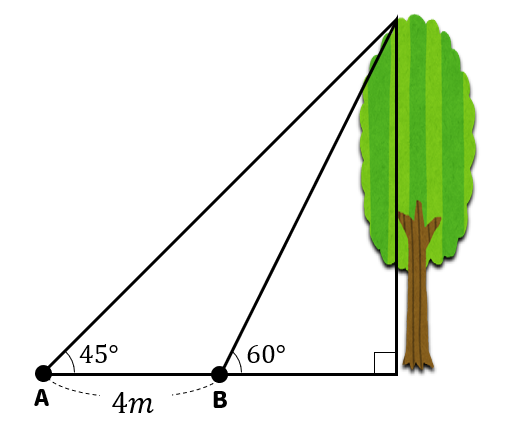
ということで、このような図になります。
木の高さを\(x\)mとして話を進めていきましょう。
まず、45°、45°、90°の直角二等辺三角形に注目しましょう。

すると、このように底辺にあたる部分も\(x\)mと表すことができます。
次に60°、30°、90°の直角三角形に注目します。
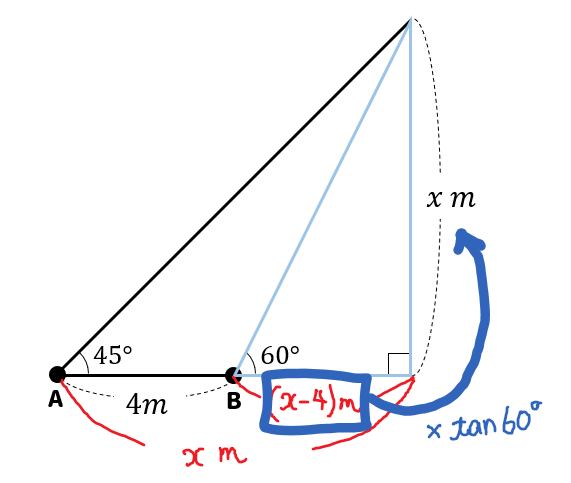
すると、底辺の\((x-4)\)に\(\tan60°\)をかけると高さが求まるので次のような式が作れます。
$$\begin{eqnarray}(x-4)\times \tan60°&=&x\\[5pt](x-4)\times \sqrt{3}&=&x\\[5pt]\sqrt{3}x-x&=&4\sqrt{3}\\[5pt](\sqrt{3}-1)x&=&4\sqrt{3}\\[5pt]x&=&\frac{4\sqrt{3}}{\sqrt{3}-1}\\[5pt]x&=&\frac{4\sqrt{3}(\sqrt{3}+1)}{2}\\[5pt]x&=&\frac{12+4\sqrt{3}}{2}\\[5pt]x&=&\color{red}{6+2\sqrt{3}}\cdots (解) \end{eqnarray}$$
木の高さを\(x\)とおいて、そこから2つの直角三角形を使いながら考えていくというのがポイントですね。
まとめ!
三角比を使って高さを求める場合には
この関係式をマスターしておくことが大事です。
\(1:1:\sqrt{2}\)や\(1:2:\sqrt{3}\)の比を使いながら高さを求めることもできるのですが
問題①のような40°といった有名角ではない場合、比では太刀打ちできなくなります。
なので、しっかりと三角比の式を覚えて使いこなせるようにしておくことが大切ですね(^^)















コメントを残す