今回は正負の数の大小関係を考えてみよう。
それでは、いきなり問題です!
3と5
どちらの数が大きいか分かりますか?
おそらく、多くの人が
5の方が大きいってことが
すぐに分かったと思います。
では、次に
-3とー5だったらどっちが大きいかな?
-0.1とー0.11だったらどうだろうか。
更に
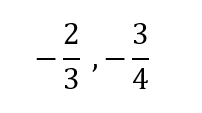
分数が出てきたらどうでしょうか。
一気に難しくなってしまいますね。
今回はこういった正負の数の大小関係を
一緒に丁寧に見ていきましょう。
大小関係を表す不等号
数の大小関係を表すときに
用いられる記号を
不等号と言います。
こんなやつですね。
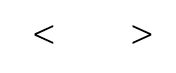
くの字みたいな記号です。
このように使います。
小 < 大 大 > 小
大きい数の方に
くの字の口が開いた方を向けて書きます。
例えば
2と3の大小関係を比べたときに
3の方が大きいので
2<3 もしくは 3>2
と不等号を用いて表します。
今回の記事では
この不等号を連発していくので
記号の意味をしっかりと理解しておいてください。
数直線を使って大小関係を考える
数の大小関係を考えるときに便利なのが数直線です。
数直線とは
こういった目盛りの入った直線のことですね。
そして、この数直線において重要なのが
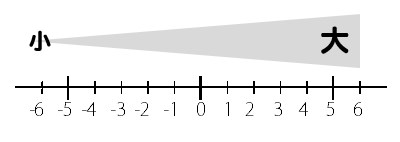
右に行けば行くほど
数は大きくなる
左に行けば行くほど
数は小さくなるってこと。
つまり
-3とー2
どっちが大きいんだろうって考えるときに
それぞれの数を数直線上に置いてみると
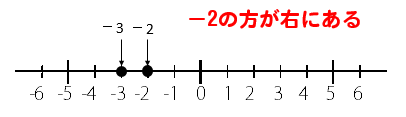
-2の方が右にあるのがわかるね
だから、-2の方が大きいってことがわかります。
不等号で表すと
-3<-2
となります。
そして
数直線を使って考えるときに
一緒に覚えておいて欲しいのが
正の数は
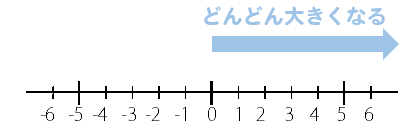
原点から離れれば離れるほど
数は大きくなる。
一方で
負の数は
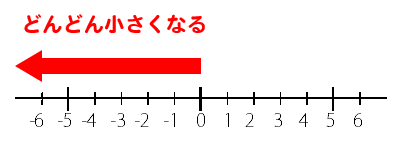
原点から離れれば離れるほど
数は小さくなる。
ちなみに
数が原点から
どれくらい離れているかを
表す数値を絶対値というから
これも合わせて覚えておいてください。
原点からの距離を表す数値
[例]-3の絶対値は ⇒ 3
原点から左に3つ離れているところにあるから3
+5の絶対値は ⇒ 5
原点から右に5つ離れているところにあるから5
正負の数の大小関係についてまとめておくと
正の数と負の数を比べる場合
正の数の方が必ず大きくなります。
正の数が大きくなるから
+2>-3 となります。
正の数同士を比べる場合
絶対値の大きい方が数自体も大きくなります。
+3の方が絶対値が大きいから(原点から離れているから)
+2<+3 となります。
負の数同士で比べる場合
絶対値が大きい方が数自体は小さくなります。
ー3の方が絶対値が大きいから(原点から離れているから)
数自体は小さくなってしまいます。
よって
ー2>ー3 となります。
- 正の数と負の数
必ず正の数が大きくなる
- 正の数同士
絶対値が大きい数が数自体も大きくなる
- 負の数同士
絶対値が大きい方が数自体は小さくなる
問題を解きながら理解を深めよう!
では
正負の数の大小関係を
見極める方法を学んだところで
実際に問題に挑戦してみましょう。
それでは問題です。
□に当てはまる不等号を書き入れなさい。
問題1
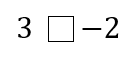
正の数と負の数の比較になるので
正の数が必ず大きくなります。
数直線で表してみても
正の数が必ず右側に来ることがわかりますね。
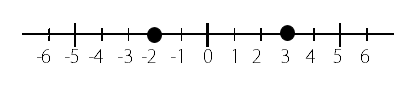
よって、答えは
問題2

正の数同士の比較になるので
絶対値が大きい方が数自体も大きくなります。
それぞれの絶対値を見てみると
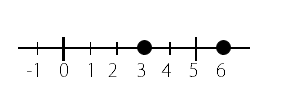
3の絶対値 ⇒ 3
(原点から3離れているから)
6の絶対値 ⇒ 6
(原点から6離れているから)
よって、絶対値が大きいのは6の方だから
答えは
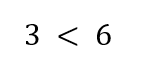
どんどん行きましょう!
問題3
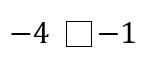
負の数同士の比較になるので
絶対値が大きい方が数自体は小さくなります。
それぞれの絶対値を見てみると
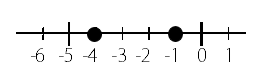
-4の絶対値は ⇒ 4
(原点から4離れているから)
-1の絶対値は ⇒ 1
(原点から1離れているから)
よって
-4の方が絶対値が大きいので
数自体は小さくなります。
だから答えは

問題4

0が出てくると困ってしまう人がいますが
落ち着いて、数を数直線上に置いて考えてみましょう。
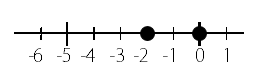
0の方が右側にくるので
答えは

発展問題で実力UP!
それでは、ここからは少し発展的な問題にも挑戦してみます。
小数の大小関係
大小関係を比べるときに
小数が出てくると嫌だなーって思いますよね。
だけど、小数であっても
基本に忠実に考えていけば大丈夫!
ー1.5とー1.2
これらの数の大小関係を比べてみましょう。
負の数同士の比較になるので
絶対値が大きい方が数自体は小さくなりますね。
では
どちらの絶対値が大きくなるか
(どちらの数が原点から遠くに離れているか)
考えてみましょう。
ー1.5は数直線上に置いてみると
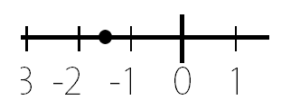
原点からは1.5離れているので
ー1.5の絶対値は ⇒ 1.5
ー1.2も同じように数直線上に置いてみると
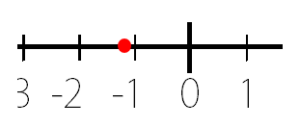
原点から1.2離れているので
ー1.2の絶対値は ⇒ 1.2
ー1.5の絶対値の方が大きいので
ー1.5の方が小さいということが分かります。
それぞれの数を同時に数直線上に置いてみても
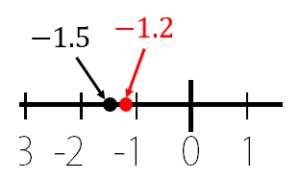
ー1.5は左側にあるので、小さいってことが分かりますね。
よって、答えは
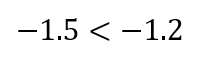
小数であっても
絶対値や数直線を使って
丁寧に考えてみれば
他の問題と同じように解くことができます!
小数だからと言って
特別な解き方があるわけではないですからね。
分数の大小関係
次は分数です。
分数…
見た目がキライ!!
そんなこと言わず
仲良くしてやってください^^;
それでは、文頭にも出てきた
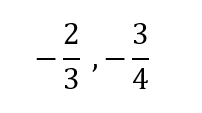
この数の大小関係について考えてみましょう。
負の数同士の比較になるので
絶対値の大きい方が数自体は小さくなります。
では、それぞれの絶対値を見てみましょう。

それぞれの絶対値は分かりましたが
ここで一つ問題が…
あれ?
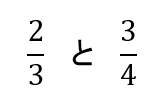
どっちが大きいんだ?
ちょっと見た目だけでは分かりにくいですね…
分数の大小を考えるときには
それぞれの分母を揃えてやると大小がハッキリとわかりやすくなります。
つまり、通分ですね。
では、それぞれの数を通分してみると
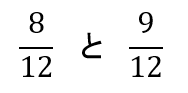
分母の数が揃うと大小関係が分かりやすくなりました。
この場合、分数の上にある分子の数を比較すると
9の方が大きいですよね
だから、数全体で考えたときも
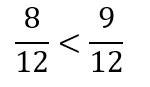
となって
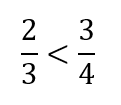
通分する前の状態の分数も
こういう大小関係だということが分かりました。
つまり

ということなので
問題にあった数の大小関係は
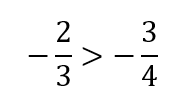
となります。
分数の大小関係を比較するときには
それぞれの数の絶対値を
通分して比較してみることがポイントですね!
3つの大小関係
今までは2つの数の大小関係について考えてきましたが
問題によっては
これらの数の大小関係を不等号を用いて表せ
+3, -5, -1
というように3つ以上の数を比較させて
大小関係を問う問題もあります。
こういった問題でよくある間違いがコレ
+3>-5<-1
このように
+3>ー5
-5<-1
を組み合わせて書いてしまうというミス。
それぞれの大小関係については間違っていません。
しかし
+3>-5<-1
この式からは
+3とー1の大小関係はどうなってるの?
っていうことが伝わってきませんよね。
だから
3つ以上の数の大小関係を表すときには
その式を見れば
すべての数の関係性が分かるようにしておかないといけません。
という訳で
答えを書くときには
数字を並べ替えて
小<中<大
というように表記します。
(大>中>小の表記でもOK)
今回の問題であれば
-5<-1<+3
と表記すればOKです!
そうすれば
ひと目見ただけで
一番小さい数はー5
真ん中の数字はー1
一番大きい数は+3
というように3つの数の関係性が正確に伝わるはずです。

正負の数の大小関係まとめ
数直線に数を置いたときに右側にある数が大きくなる。

正の数と負の数の比較は、必ず正の数が大きくなる。
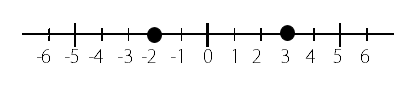
正の数同士の比較は、絶対値が大きい方が数自体も大きくなる。

負の数同士の比較は、絶対値が大きい方が数自体は小さくなる。

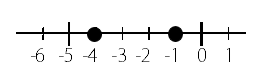
小数の比較であっても上と同じような考え方で解くことができる。
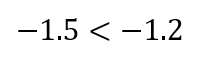

分数の場合は、通分を活用して大小関係を見極めよう。
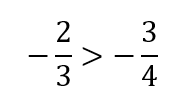
それぞれの絶対値を通分して比較してみれば
大小関係がわかりやすくなります。

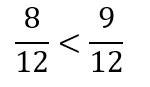
3つ以上の数の大小関係を表すときには
小さい順に数を並び替えてから
不等号を用いて表記する。
小<中<大
-5<-1<+3
以上が正負の数の大小関係についてでした。
あとは、たくさん問題を解いていきながら
理解を深めていきましょう!
- 正負の数とは?
- 絶対値とは?
- 大小関係を不等号で表すためのポイント ←今回の記事
- 加法・減法をマスターしよう!
- 乗法・除法をマスターしよう!
- 累乗の計算とは
- 正負の数、分数計算のやり方を問題解説!
- 正負の数の利用、平均を使った問題を解説!
- 正負の数の問題まとめ!計算のやり方を確認しよう!
★上級者向け★


















コメントを残す