この記事では、小学生で学習する知識だけを利用して
30度の角を持つ三角形の面積を求める方法について解説していきます。
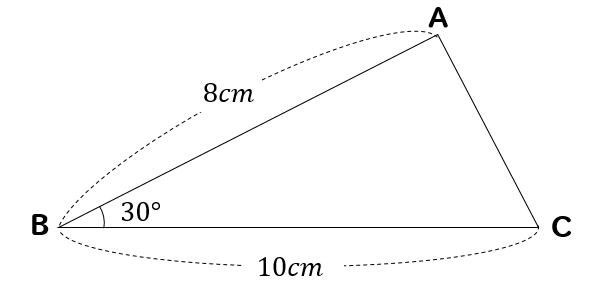
三角形の面積は
$$\LARGE{(底辺)\times (高さ)\times \frac{1}{2}}$$
で求めることができましたが。
この三角形を見る限り、高さがどこにも書いていませんね。
この状況でどうやって面積を求めれば良いのでしょうか。
30度の三角形の特徴を学びながら
面積を求める方法について身につけていきましょう！
30度三角形の辺の比
今回の問題を解く上で、知っておきたい
30度三角形の特徴があります。
それがコレ！
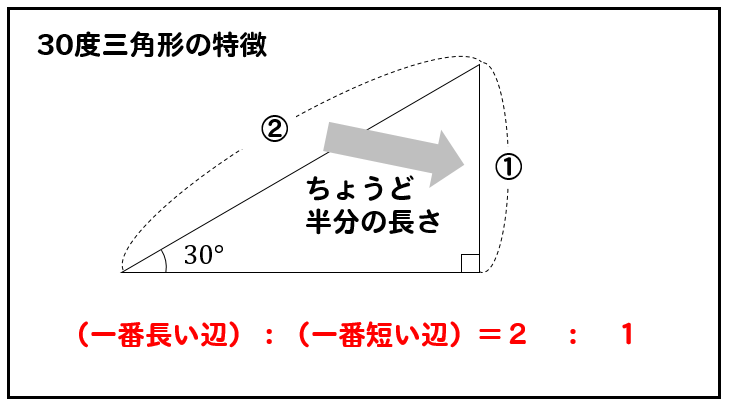
30度の角を持つ直角三角形の
一番長い辺と一番短い辺の比は\(2:1\)になるという特徴があります。
つまり、一番短い辺は、一番長い辺のちょうど半分になるわけですね。
例えば、一番長い辺が10㎝の30度直角三角形であれば
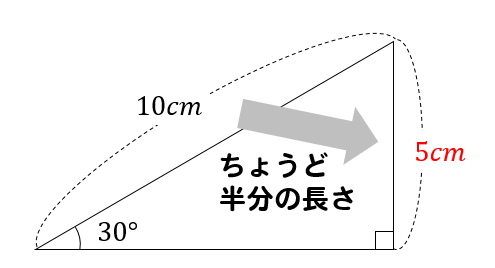
このように一番短い辺の長さは、10㎝の半分である5㎝となります。
逆もありだからね。
一番短い辺の長さが分かっている場合には
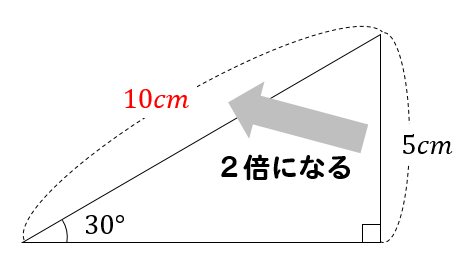
このように2倍することで、一番長い辺の長さを求めることもできます。
この2つの辺は、\(2:1\)の関係があるんだっていうことを知っておいてください。
これを利用すると、いろいろと便利なんだよね(^^)
辺の比が2:1になる理由
そもそも、なんで辺の長さが\(2:1\)になるの？
っていう疑問が湧いてくるよね。
ここでは、かんたーんに説明しておくから
あ、そうなんだ。ふーん。
って感じで、頭の片隅にでも置いておいてください。
実は、30度の直角三角形って
正三角形を半分にした三角形なんだよね。
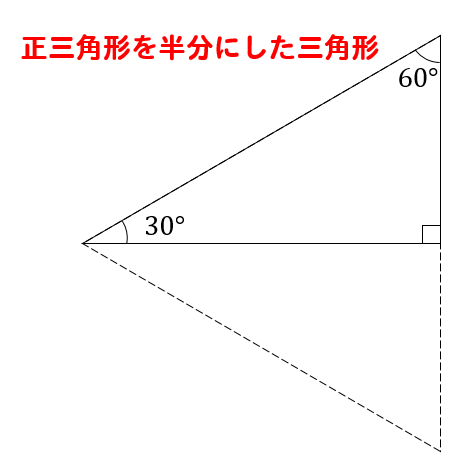
1辺の長さが10㎝の正三角形を考えた場合
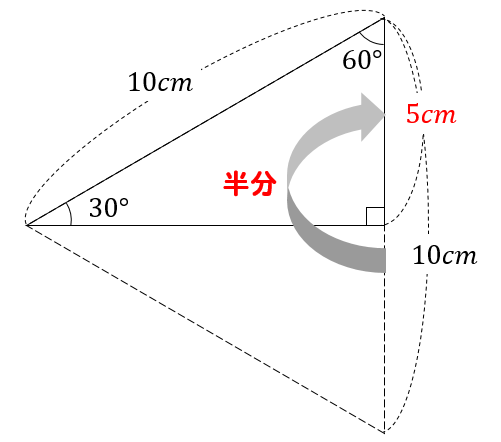
30度の直角三角形の一番短い辺の長さは10cmの半分である5㎝になるってことがわかるよね。
だから、このような辺の関係になるんだね。
30度の直角三角形は、正三角形を半分にした三角形であるってことを理解しておけば、辺の比については理解できるはずです(^^)
辺の比を利用して高さを求める
それでは、問題に戻って
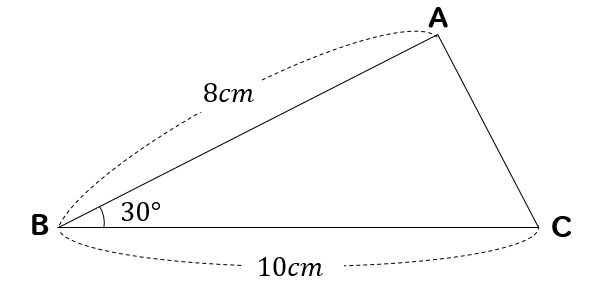
こちらの三角形の面積を求めていきましょう。
このように高さとなる線を引いてやると
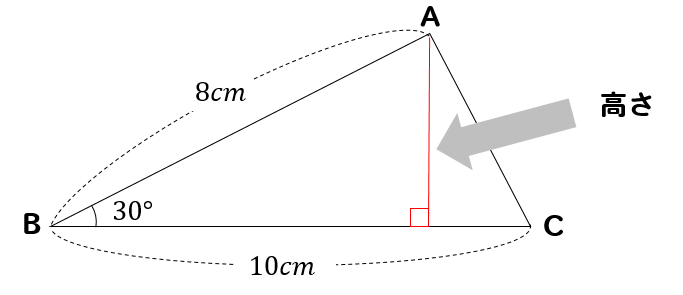
30度の直角三角形を見つけることができますね！
よって、辺の比の特徴を利用すると
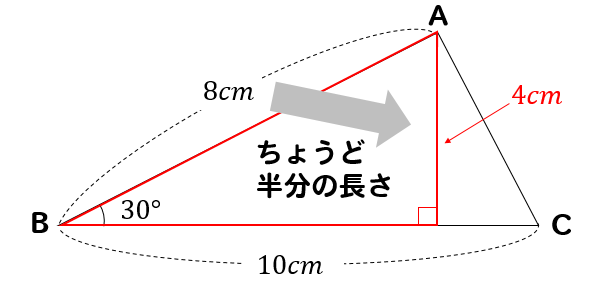
このように高さが4㎝であることがわかります。
高さが分かってしまえば、こっちのもんですね！
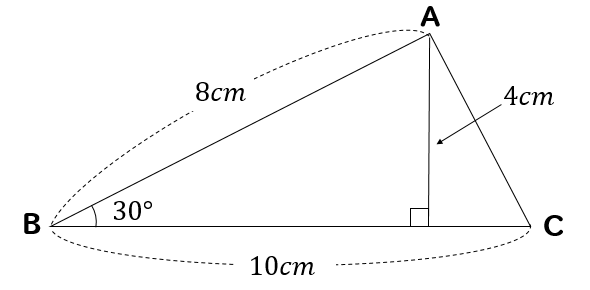
三角形の面積は
$$\LARGE{10\times 4\times \frac{1}{2}}$$
$$\LARGE{=20(cm^2)}$$
となりました。
こんな感じで、辺の比を利用しながら面積を求めるのに必要な長さを求めていきます。
それでは、理解を深めるために練習問題に挑戦してみましょう！
30度面積の練習問題
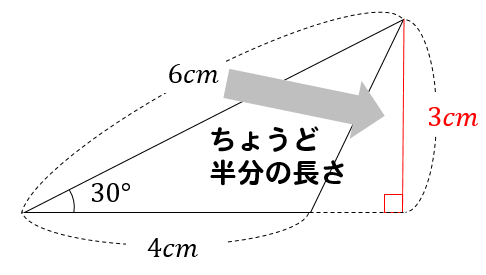
次の三角形の面積を求めなさい。
答え
$$6(cm^2)$$
高さは、このように3㎝となるから
$$\LARGE{4\times 3\times \frac{1}{2}}$$
$$\LARGE{=6(cm^2)}$$
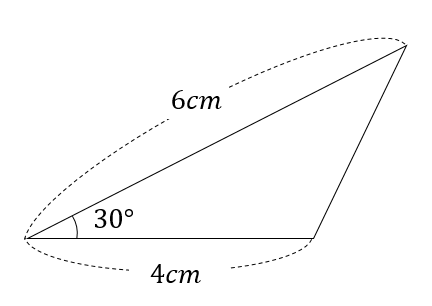
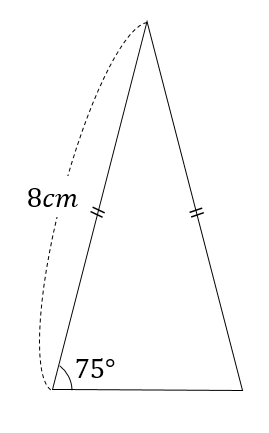
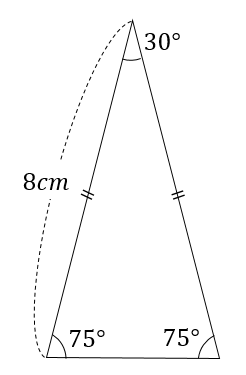
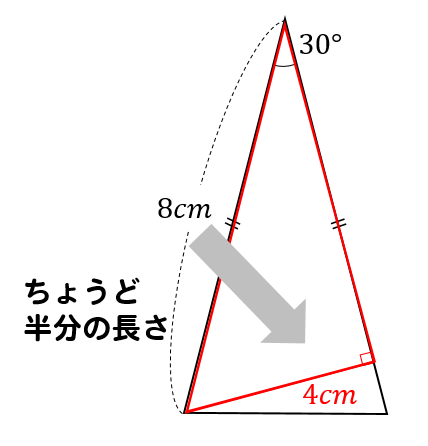
次の三角形の面積を求めなさい。
答え
$$16(cm^2)$$
まずは、二等辺三角形の性質を利用して
30度の角があることを発見しないといけません。
30度の角があることが分かれば、線を引いて直角三角形を作ります。
すると高さは、このように4㎝となるから
$$\LARGE{8\times 4\times \frac{1}{2}}$$
$$\LARGE{=16(cm^2)}$$
まとめ
お疲れ様でした！
30度の直角三角形では
このように一番長い辺と一番短い辺の比を利用することで
問題を解く上で必要な情報を読み取ることができます。
特に算数で扱う問題では、この性質を利用して
三角形の高さを求めさせることが多いです。
30度の角を発見したら、線を引いて直角三角形を作ってやることがポイントです。
しっかりと覚えておきましょう！
それでは、今回はここまで！
たくさん練習して、一人でも解けるようにしておこうね。
ファイトだー(/・ω・)/
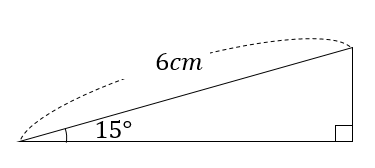
30度三角形をマスターしたら
次は、15度三角形の面積を求める方法もどうぞ！
裏ワザ公式を学べる参考書！？
今回紹介した30度三角形の問題の他に
中学受験では、身につけておきたい公式や裏ワザ解法なるものがたくさんあります。
それらのほとんどは、学校の授業では扱っておらず
塾や家庭教師の先生からこっそりと学ぶこととなります。
つまり
塾に行っている人だけが得をする！？みたいなね。
そんなのズルいよね
塾に行かなくても、中学受験に必要な公式や裏ワザ解法を学べないかなと考えていたところ
ちょうど良い参考書を見つけました！
それがこの参考書です。
紹介されている公式や裏ワザ公式はこんな感じです。
ケーキの法則
センターライン解法
ピックの定理
台形ペケポン！？
魔女のぼうし！？
イナズマ型の角度とは？
などなど
気になる裏ワザ解法が盛りだくさんです。
聞いただけでは、ほんとに算数をやってんのか！？
って思っちゃうような言葉ばかりですけどねｗ
ほんと目からウロコです。
知らない人は損してるーって感じです。
そして
この参考書の良い点は、公式や裏ワザ解法がまとめられているだけでなく
演習がたくさんできるように問題が豊富に用意されていることです。
裏ワザだけ学んでも、どこでどのように活用すればよいのか分からなかったら意味がないもんね。
しっかりと問題演習を通して理解を深めれるようになっています。
もちろん、この記事で紹介した30度問題についても詳しく解説されているので
もっと問題演習したいという人は、この本を利用してみてはいかがでしょうか(^^)
理科バージョンもおススメです！
コメントを残す