今回は、中1で学習する「資料の活用」から
ここで登場する用語や問題などを解説していきます。
定期テストの対策はこれでバッチリだ!
がんばって学習していきましょー
度数分布表とは
次の資料は、ある中学校の1年生が数学の小テストをした結果を表したものです。
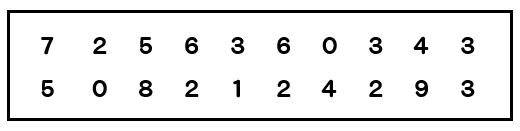
うーん、点数を並べられているだけだと特徴が掴みにくくて、よくわかりません。
そこで、みんなの得点を整理して分かりやすく表にまとめていきます。
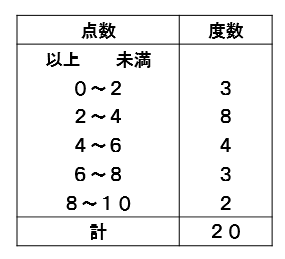
このように、資料をいくつかの区間(階級)に分けて、その区間ごとにどれくらいのデータが入っているか(度数)を示し、資料の散らばり具合などを分かりやすく表にまとめたものを度数分布表といいます。
表にすると、みんながどれくらいの点を取っているのかがわかりやすいよね!
それでは、度数分布表を扱う上で知っておきたい用語をいくつか紹介していくよ
階級とは
資料を整理するための区間のことを階級といいます。

階級の幅
そして、この区間の幅のことを階級の幅といいます。
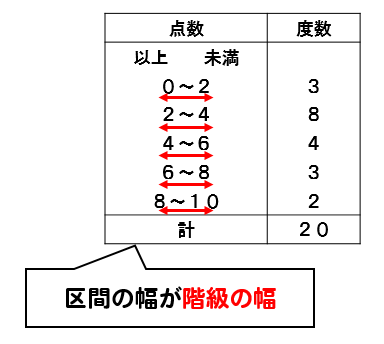
今回の資料であれば、2点ごとに階級を分けているので階級の幅は2点となります。
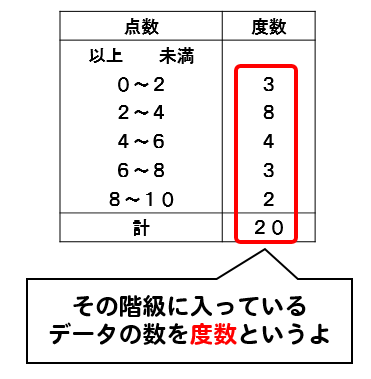
度数とは
それぞれの階級に入っている資料の数のことを度数といいます。
階級値とは
階級の中央の値をその階級の階級値といいます。
例えば
0点以上2点未満の階級の階級値は1点
10点以上13点未満の階級の階級値は11.5点
となります。
階級値の求め方
階級値は、小数になってしまうことも多く計算ミスが起こりやすい値の1つです。
パッと階級の真ん中の数値を計算できないときには、次の計算式に当てはめて考えていきましょう。

この計算式を利用すると
0以上5未満の階級の階級値は
$$\LARGE{\frac{0+5}{2}=5\div2=2.5}$$
13以上17未満の階級の階級値は
$$\LARGE{\frac{13+17}{2}=30\div2=15}$$
このように階級値を求めることができます。
小数が出てくると暗算で計算しにくい場合もあるので、そんなときには上の計算式を利用してみてください。
範囲(レンジ)とは
資料に含まれている最大の値から最小の値をひいた差を範囲(レンジ)といいます。
レンジという言葉を使うことは少ないんだけど
たまに範囲ではなく、あえてレンジという言葉を使う問題もあるので注意してください。
今回の資料であれば
最低点は0点、最高点は9点なので範囲は
$$\LARGE{9-0=9(点)}$$
となります。
ヒストグラムとは
度数分布表を使うことで、資料の散らばり具合などが分かりやすくなりましたが、もっと見た目でわかりやすくするためにグラフにしていきます。
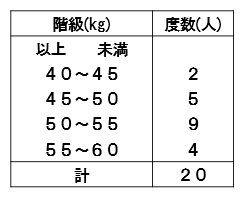
この度数分布表をグラフ化していくと
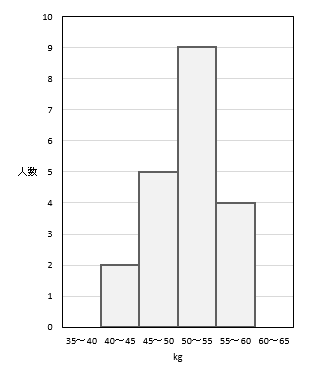
このようになり、これをヒストグラムといいます。
階級の幅を底辺
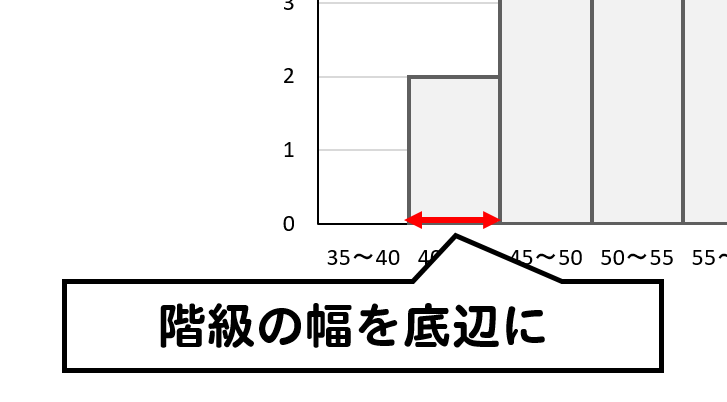
度数を高さとする
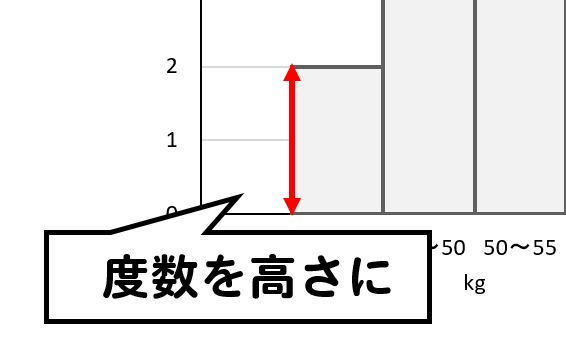
長方形で表したグラフのことです。
こうやって、ヒストグラムを活用することで
誰がどう見ても一発でどこが多い少ないっていうのがわかるよね!
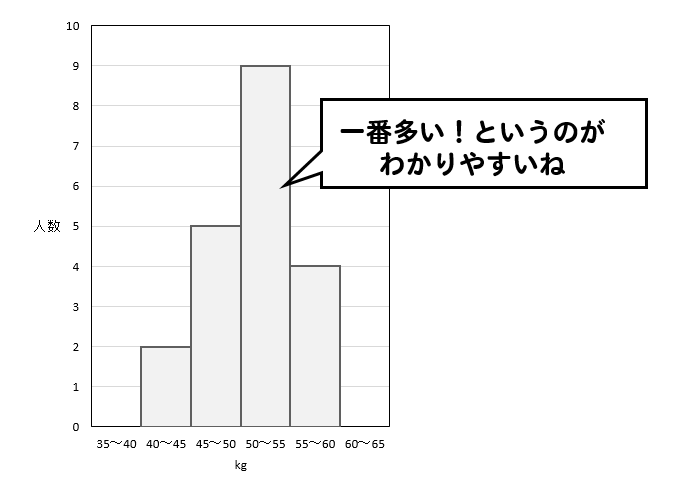
度数折れ線とは
度数折れ線とは、ヒストグラムの各長方形の上の辺の真ん中の点をとって
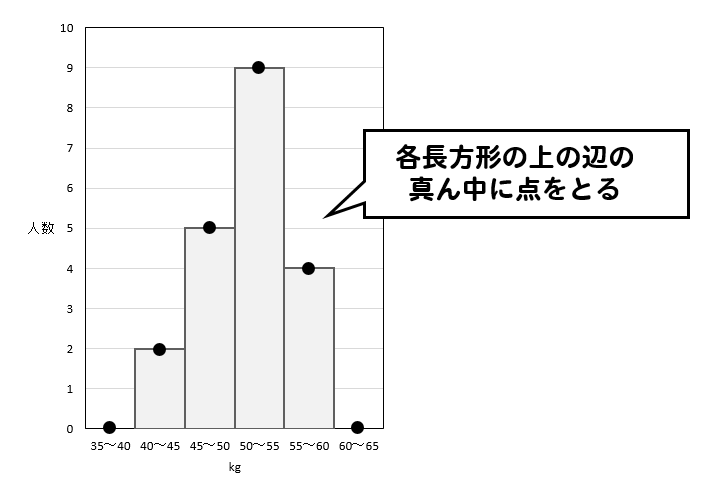
それぞれを順に結ぶことでできる折れ線のことを度数折れ線、または度数分布多角形といいます。
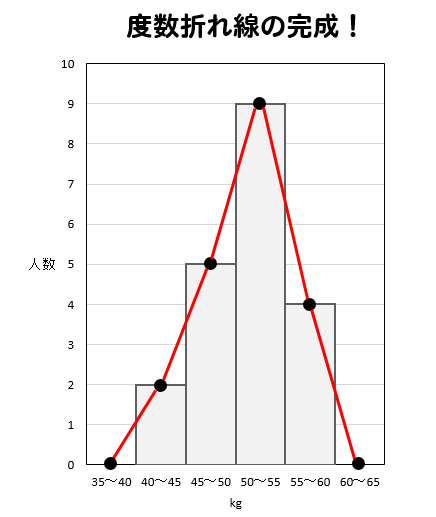
度数が0のところも点を取らないといけないから気をつけてね!
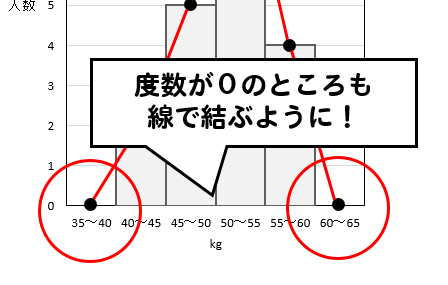
相対度数とは
各階級の度数が、全体の中でどれだけの割合にあたるかを示す値を相対度数といいます。

このような計算をすることで求めることができます。
例えば、このような資料を考える場合
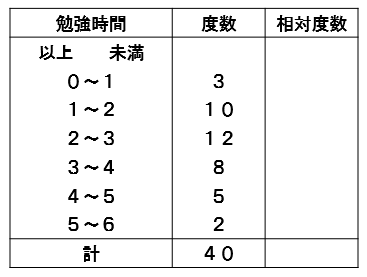
勉強時間が0以上1未満の階級の相対度数は
$$\LARGE{\frac{3}{40}=3\div 40=0.075}$$
と、このように求めることができます。
他の階級も同様に計算すると
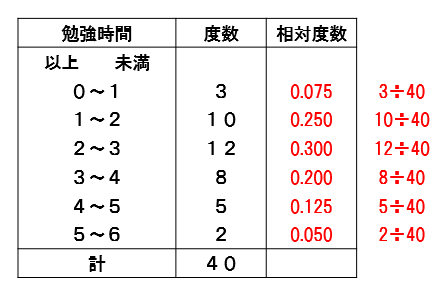
このようになります。
相対度数を表すときに気をつけたいのは
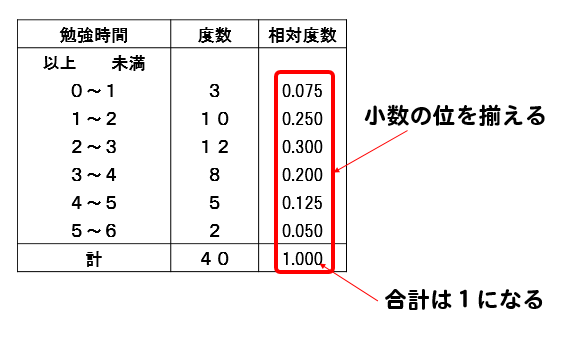
このように、相対度数の小数の位は揃えて表すようにしましょう。
そして、それぞれの階級の相対度数は合計すると1になります。
もしも、計算してみて1にならなければ、どこかがミスしているということになります。
テストのときには必ず確かめとして活用してください。
相対度数を利用する度数の求め方
相対度数を利用することで、その階級の度数を求めることができます。

例えば、このような資料を考える場合
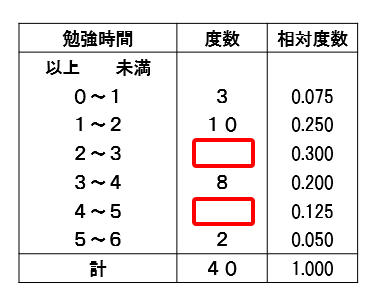
勉強時間が2以上3未満の階級の度数は
$$\LARGE{40\times 0.300=12}$$
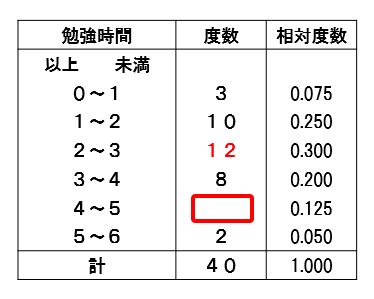
と、求めることができます。
勉強時間が4以上5未満の階級の度数は
$$\LARGE{40\times 0.125=5}$$
相対度数を利用して、このように求めることもできますが
他の階級の度数がすべてわかっている状況なので
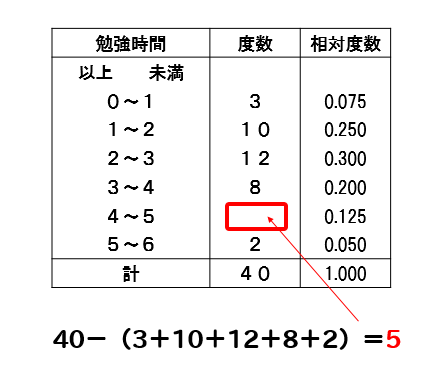
このように計算してやった方が楽ですね!
相対度数については、こちらの記事でも詳しく解説しているので参考にしてみてください(^^)

代表値とは
資料を1つの値で代表させて、資料の特徴を読み取ったり、他の資料と比較したりする場合があります。この代表となる値のことを代表値といいます。
この代表値には、平均値や中央値、最頻値といったものがあります。
平均値の求め方
資料全体の平均の値を平均値といいます。

このように求めることができます。
例えば、このような資料の平均を求める場合には

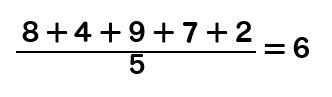
と、求めることができます。
度数分布表から平均値を求める場合には
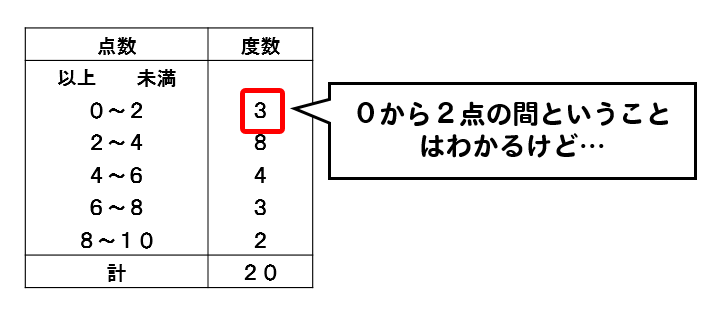
各階級に入っている度数はわかるんだけど、それぞれのデータの値がはっきりとはわからないので資料の値を合計することができません。
こういう場合には、階級値を利用して平均値を求めていきます。
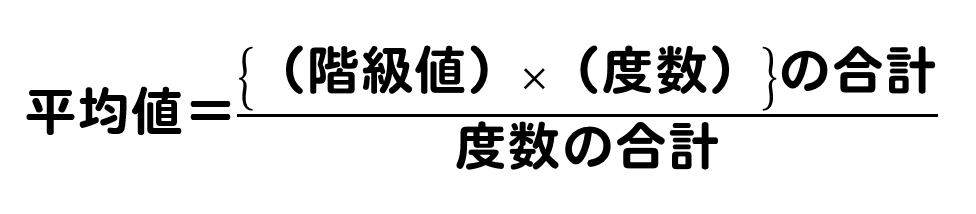
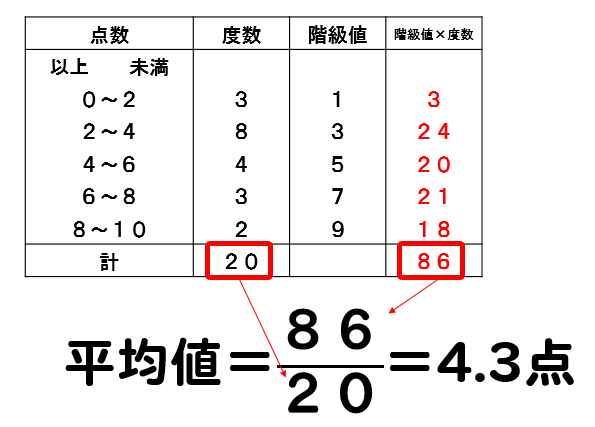
その階級に入っている値をすべて階級値の値だと考えて、計算をしていきます。
中央値(メジアン)の求め方
資料を大きさ順に並べたときの中央の値を中央値またはメジアンといいます。
それぞれの資料の中央値を求めてみましょう。

中央値を求めるためには、資料を大きさ順に並べ替えます。
資料の個数が奇数の場合
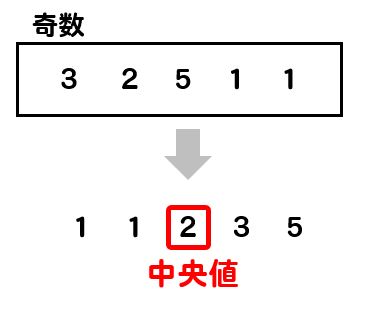
このように真ん中に位置する資料の値が中央値となります。
一方、資料の個数が偶数の場合
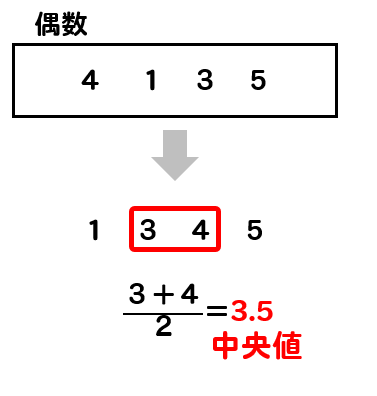
真ん中にある値を1つに決められません。
そのため、真ん中にある2つの資料の値を見て、その平均をとります。
資料の個数によって、中央値の求め方が少し変わってしまうので気をつけてください。
資料が奇数 ⇒ 値が1つ決まる
資料が偶数 ⇒ 真ん中にある2つの値の平均をとる
中央値に関しては、こちらの記事でも詳しく解説しているのでご参考ください(^^)
最頻値(モード)の求め方
資料の値の中で、もっとも多く現れる値のことを最頻値またはモードといいます。
次の資料では

2が一番多く現れる値なので

最頻値は2となります。
度数分布表から最頻値を判断する場合には
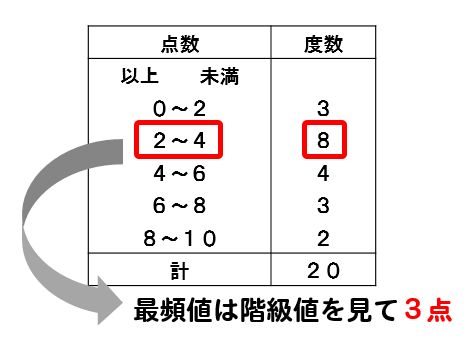
度数の一番大きい階級の階級値を最頻値とします。
近似値とは
真の値に近い値を近似値といいます。
例えば、自分が定規などで測った値であったり、四捨五入して得られた値というのは真の値(正確な数値)とは言えませんよね。ちょっと誤差があったりするはずです。だけど、大きな違いがあるわけではなく真の値に近い数値ということができます。
このように、真の値ではないんだけど、それに近い値のことを近似値といいます。
誤差とは
近似値と真の値との差を誤差といいます。

誤差を考える問題では以下のようなものがあります。
問題
ある数の小数第1位を四捨五入して25になった。このとき、誤差の絶対値は大きくてどれくらいになるか答えなさい。
小数第1位を四捨五入して25になるということは
$$24.5≦(ある数)<25.5$$
ということになります。
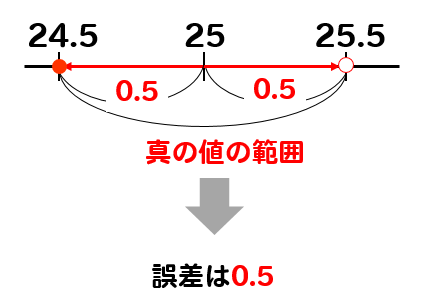
つまり、一番離れている数でも24.5となるので誤差は0.5となります。
有効数字とは
近似値を表す数字のうち、信頼できる数字のことを有効数字といいます。
信頼できる数字ってなに??って思いますよね。
例えば、真の値が16.342㎝の物を定規を使って長さを測定するとします。

すると、大体の定規って1㎜までの単位までしか測定できないので
16.3㎝という測定結果となるはずです。
本来なら16.343㎝なので、測定結果には少し誤差が生じており近似値となります。
つまり、今回の測定結果では

小数第1位までは、正確に測定できており
それ以降の数は正確には測定できなかったということになります。
ということで、有効数字は1、6、3となります。
このように正しく測定できており、信頼できる数のことを有効数字といいます。
そして、有効数字は

の形で表します。
具体例を示しておきますね。
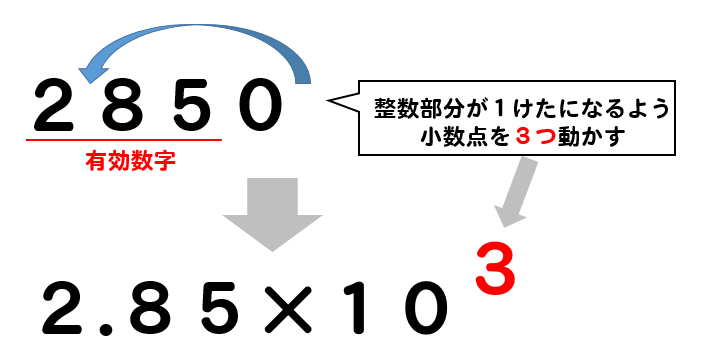
2850gの有効数字が2,8,5のとき
$$\LARGE{2.85\times 10^3(g)}$$
まとめ
お疲れ様でした!
中学で学習する資料の活用の用語をまとめていきました。
覚えなくてはいけない言葉が多い単元なので
しっかりと意味を確認しながら、それぞれの値を正確に求めれるよう練習を重ねていきましょう。
特にテストでは
相対度数、平均値、中央値
といった値を求めさせる問題がよく出題されます。
しっかりと練習して、身につけていきましょう!
ファイトだー(/・ω・)/











めっちゃ分かりやすかったです♥
明日、テストで出るので解き方が理解出来ていなくて困っていました( ˙-˙ )
字だけでなく、表も書いてくれているので最後まで見やすかったです⭐
覚えるのが大変ですね
頑張ります( `ω´ )
ありがとうございます(^^)
そう言っていただけると、頑張って記事を書いてよかったです!
本日がテストですよね、上手くいくことを願っています。
ファイトだ(/・ω・)/
メッサわかりやすい。透視図で数学も必要と思いいろいろ検索。痒いとこに手が届く感じ。うざいってなった所でちょうどお疲れさんです。も良い。
ありがとうございます!
内容が多くなってしまいましたが
記事の中に最後まで盛り込むことができて良かったです(^^)
ありがとうございます
テストの参考になり、良かったです。
テスト勉強お疲れ様です!
お役に立てたようで嬉しい限りです(^^)
いやぁ…このサイトあって助かりました!
お役に立てて嬉しいです(/・ω・)/
とてもわかりやすかったです!
前テストだったんですけど、おかげで100点を取ることができました!
本当にありがとうございました
100点!?
すごいですね!!
少しでもお役に立てたのなら嬉しい限りです(^^)
最近やってなかったんですっかり忘れてました笑笑ありがとうございます!
よい復習になったようで良かったです(^^)
頑張ってください!
詳しく書いてあってわかりやすいです!!
今後も頑張って下さい
ありがとうございます!
がんばって記事を書いていきますね(/・ω・)/
復習できて良かった。
お役に立ててよかったです^^
めちゃわかりやすい!テストあるので助かりました!!!
ありがとうございます!
テストがんばってくださいね^^
疑問が解けました!
中央値のところで、「メジアンいいます」ってなってます!
お恥ずかしい…訂正しておきました!
ご指摘ありがとうございます!!
エラーが起きてます( ; ; )
え、マジですか…どこの部分でしょうか?
ありがとうございます頑張って下さい
はい、がんばります!!
ありがとうございます
こちらこそ!!
このサイトあって、良かったです♪
助かりました!!
お役に立ったようで嬉しいです^^
とてもわかりやすくてためになりました!
おかげでテストはばちっりでした!
お役に立てて良かったです^^
テストばっちり嬉しいな~(‘ω’)ノ
テス勉に使わせてもらいました。
データの利用は苦手だったけどこれなら大丈夫そうです。
ありがとうございます。
テストお疲れ様でした!
お役に立てて良かったです^^
ほんとに助かった!!
データの活用&利用を学校で習って「テスト大丈夫かな?」と心配していたのですが、このサイトをみたら「あっ、これ簡単~」みたいな感じでスラスラと復習プリントが解けたので安心してテストに取り組むことが出来そうです!ありがとうございます!
長文失礼しました!
お役に立てて嬉しいです!
テストが上手くいくことを願ってますよ^^
本当に役に立ちましたありがとうございます!☆*:.。. o(≧▽≦)o .。.:*☆
お役に立てて嬉しいです^^
習ったことの復習とまとめが出来て良かったです!ありがとうございます
受験前で不安たくさんだったけど分かりやすくて理解出来て、少し自信が着きました!ありがとうございます、