【中学数学】放物線と直線の面積を求める公式は？

今回は、中学3年生で学習する二乗に比例する関数の単元から

『放物線と直線の面積』

についての問題を解説していきます。

取り上げる問題はこちら！

下の図は、関数\(y=ax^2\)のグラフ上に2点A、Bがある。点Aの座標は\((-2,2)\)で、点Bの\(x\)座標は4である。次の問いに答えなさい。

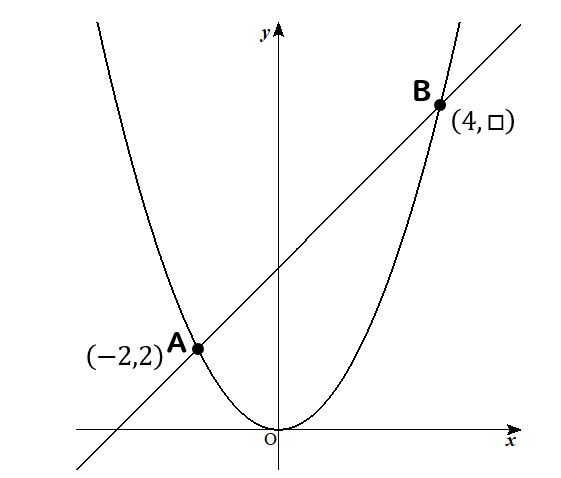
（1）\(a\)の値を求めなさい。

（2）点Bの\(y\)座標を求めなさい。

（3）直線ABの式を求めなさい。

（4）△AOBの面積を求めなさい。

入試にもよく出題される問題だから、しっかりと解けるようになりましょう！

今回の内容はこちらの動画でも解説しています(/・ω・)/

（1）\(a\)の値を求める問題解説

放物線上にある点から、\(x,y\)ともに分かっている座標を見つけます。

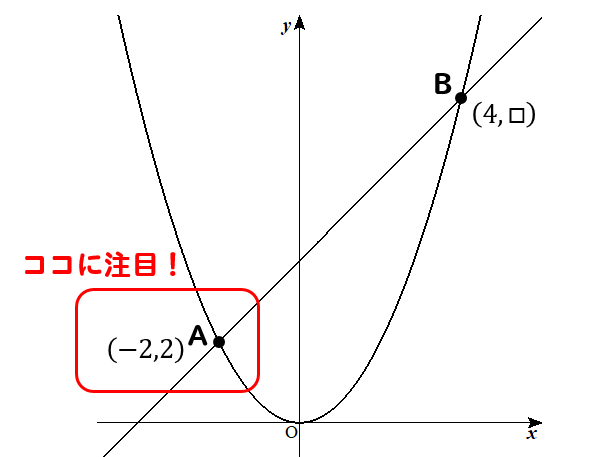
すると点Aの座標から

\(y=ax^2\)の放物線は、\(x=-2\)のとき\(y=2\)になるということが読み取れます。

そこで、\(y=ax^2\)に\(x=-2\)と\(y=2\)を代入してやります。

$$2=a\times (-2)^2$$

$$2=4a$$

$$a=\frac{1}{2}$$

となりました。

放物線の式を完成させる問題では、このように座標を見つけて代入してやればOKですね(^^)

簡単、簡単～♪

（2）座標を求める問題解説

（1）より、放物線の式が\(\displaystyle{y=\frac{1}{2}x^2}\)であることが分かりました。

この式を利用して解いていきましょう。

点Bの\(x\)座標が4であるから、その\(y\)座標を求めたいのであれば

\(\displaystyle{y=\frac{1}{2}x^2}\)に\(x=4\)を代入してやればOK

$$y=\frac{1}{2}\times 4^2$$

$$y=\frac{1}{2}\times 16$$

$$y=8$$

となりました。

今回のように、片方の座標が分かっていてもう一方の座標を知りたい！

というときには、その座標がある関数の式に代入してやればOKですね。

（2）答え

$$8$$

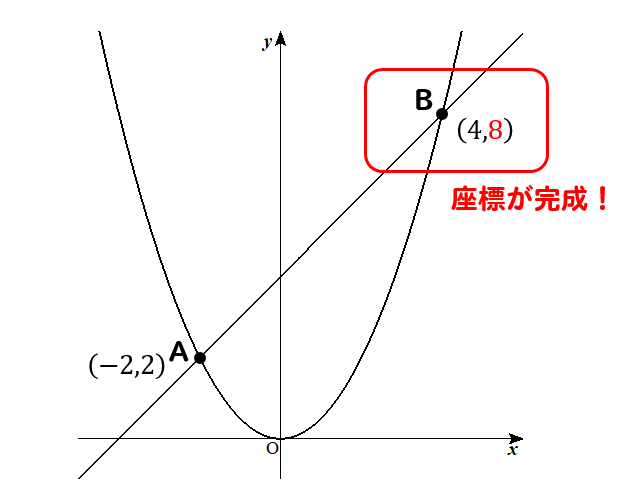
（3）直線の式を求める問題解説

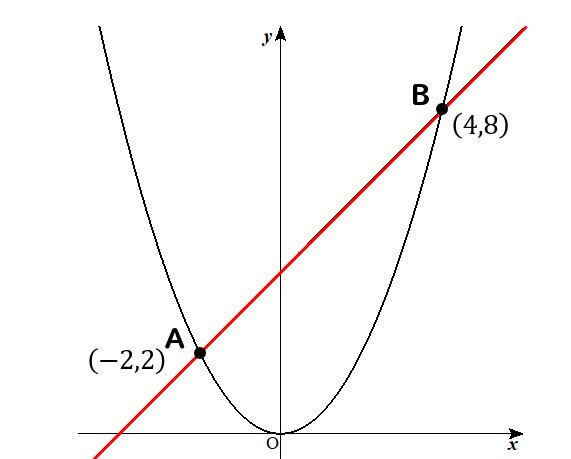
2点\((-2,2)\)、\((4,8)\)を通る直線の式を求めろということですね。

直線の式を求める方法について忘れてしまった方はこちらの記事で復習しておきましょう。

＞【一次関数】式の作り方をパターン別に問題解説！

\(y=ax+b\)の式に\((-2,2)\)、\((4,8)\)をそれぞれ代入して解いていきましょう。

\((-2,2)\)を代入すると

$$2=-2a+b$$

\((4,8)\)を代入すると

$$8=4a+b$$

それぞれの式を連立方程式で解いていきます。

\begin{eqnarray} \left\{ \begin{array}{l} -2a + b = 2 …①\\ 4a + b = 8 …②\end{array} \right. \end{eqnarray}

①－②をしてやると

$$-6a=-6$$

$$a=1$$

これを①に代入すると

$$-2+b=2$$

$$b=4$$

となります。

よって、直線ABの式は\(y=x+4\)となりました。

直線の式を求める場合には、2点の座標を読み取ってそれらを利用すれば簡単に求めれますね。

（4）面積を求める問題解説

さぁ、いよいよ本番！といった感じですね。

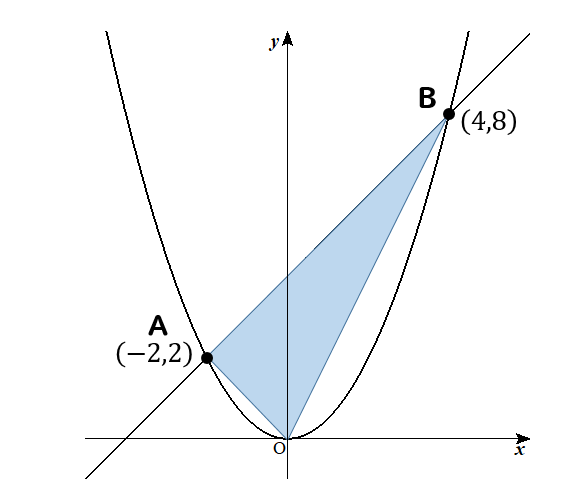
このように斜めになっている三角形の面積を求めるためには

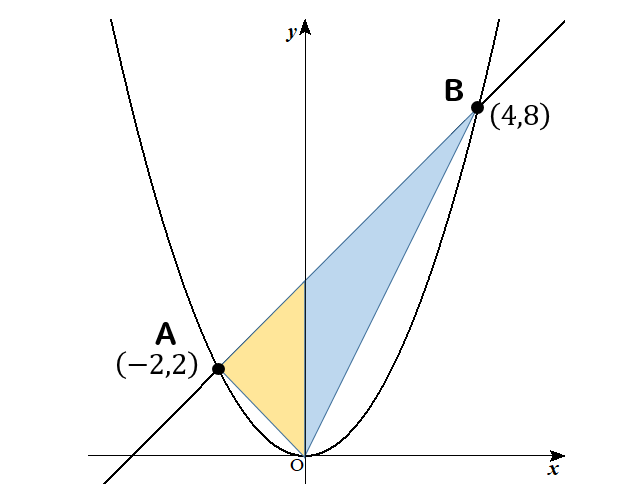
２つの三角形に分けて考えていきます。

そして、それぞれの三角形の底辺と高さを次のように決めて面積を求めていきます。

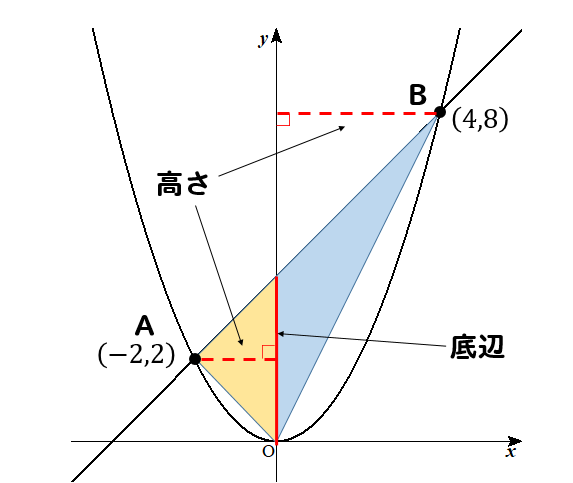
まずは、青の三角形から求めていきましょう。

直線の式が\(y=x+4\)であり、切片が4であることから

底辺の長さが4であることが分かりますね。

そして、高さに当たる部分はヨコの長さだから点Bの\(x\)座標に注目すると、4であることが分かります。以上より

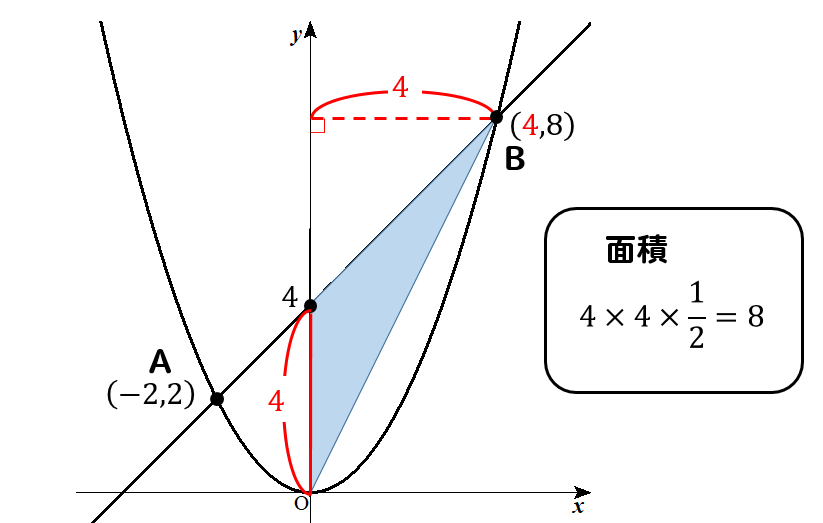
同じように黄色の三角形も面積を求めます。

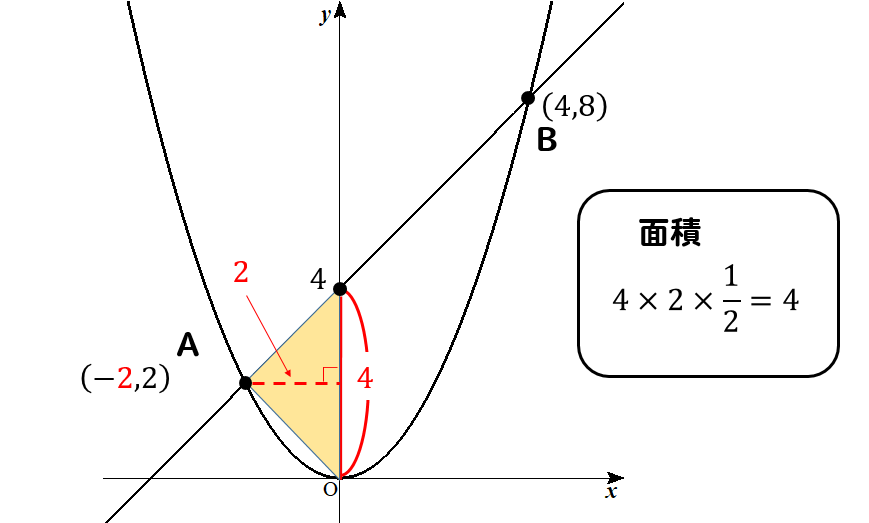
それぞれの面積を合わせたものが△AOBの面積になるから

$$△AOB=4+8=12$$

となりました。

このように2つの三角形に分けて考えてくださいね！

底辺や高さを取るのが難しく感じるかもしれませんが、そこは慣れです。

たくさん問題を解いて、やり方を身につけていきましょう。

放物線と直線の面積公式

2つの三角形に分けて面積を求めるなんて面倒だな…

そう感じているアナタ！

朗報です。

この面積を一発で求めることができる公式があります。

それがコレ！

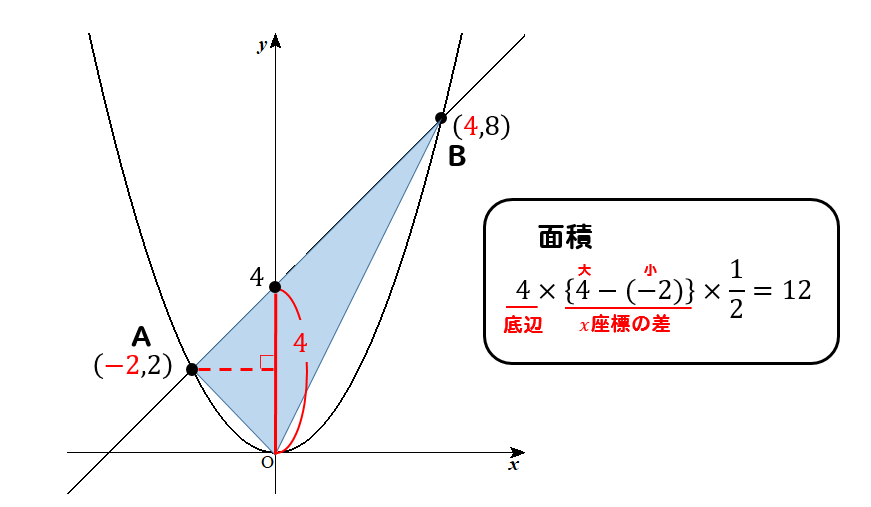
こんな感じで、一発計算をすることができます。

ただし！

やっていることは上で紹介したような三角形を二つに分けて求めているものと同じになります。

なので、こんな公式を覚えるよりかは基本に沿って、2つの三角形に分けて丁寧に解いていく方がおススメです。

座標が分からない応用問題の考え方

放物線\(\displaystyle{y=\frac{1}{2}x^2}\)と直線\(y=x+4\)の交点をそれぞれA、Bとするとき、△AOBの面積を求めなさい。

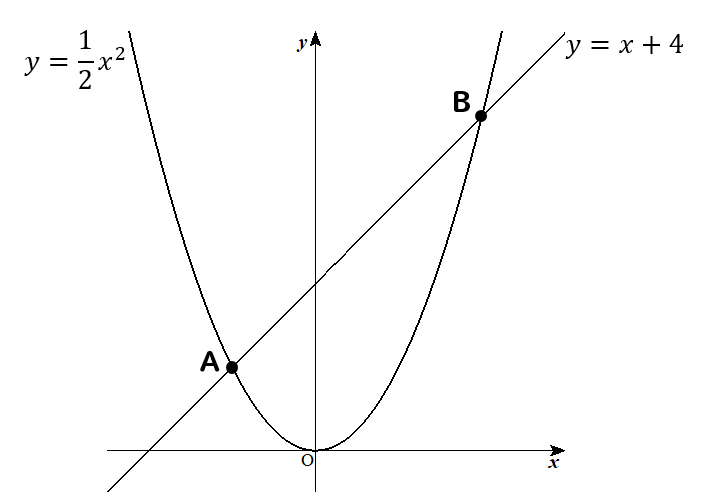
この問題では、ちょっと困ったことがありますよね…

座標が分からん！！

ということです。

2点A、Bの座標が分からんことには面積を求めることができません。

こういう場合には、連立方程式を利用して放物線と直線の交点である点A、Bの座標を求める必要があります。

詳しくはこちらの記事で解説しているので参考にしてくださいな！

＞【放物線と直線】交点の座標の求め方とは？解き方を問題解説！

\begin{eqnarray} \left\{ \begin{array}{l} y=\frac{1}{2}x^2 …①\\ y =x+4  …②\end{array} \right. \end{eqnarray}

②を①に代入すると

$$\frac{1}{2}x^2=x+4$$

$$x^2=2x+8$$

$$x^2-2x-8=0$$

$$(x-4)(x+2)=0$$

$$x=-2,4$$

よって、点A、Bの\(x\)座標はそれぞれ－2と4であることが分かりました。

ここまでくれば、あとは上で紹介したようなやり方で面積を求めることができますね。

交点の座標が分からない場合には、それぞれの関数の式を使って連立方程式で求めてやりましょう。

まとめ

お疲れ様でした！

今回取り上げた問題は、定期テストや入試によく出てきますよー！

しっかりとマスターしておきましょう。

問題の性質上、どうしても一次関数の知識も必要になります。

グラフ苦手だなーって方は一次関数を基礎から見直しておくことも大事になりますね。

一次関数の復習はこちらから！

＞中学2年生の学習記事一覧

ファイトだ(/・ω・)/