今回は高校数学Ⅱで学習する対数の単元から
『logの方程式』
について学習していきましょう。
今回取り上げる問題はこちら!
次の方程式を解け
(1)\(\log_{2}(x-1)=3\)
(2)\(2\log_{3}(x-3)=\log_{3}x+\log_{3}4\)
(3)\(\log_{3}(x-2)+\log_{3}(x-3)=2\log_{9}(x+1)\)
(4)\((\log_{3}x)^2+\log_{3}x^2=15\)
この記事を通して、これらの問題が解けるようにしていきましょう!
対数方程式についてサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
底、真数条件とlogの式変形

\(\log\)を扱う上で気を付けておかなければいけないことがあります。
それが、底と真数条件です。
底とは、\(\log\)のすぐ右下についている小さい数のことですが、ここにくる数は必ず1以外の正の数になります。
そして、底の右にある真数という数は必ず正の数になります。
\(\log\)の方程式を解くためには、これらの条件をしっかりとおさえておく必要があります。
\(\log_{a}M\)において
$$a>0 かつ a\neq1$$
$$M>0$$
そして、\(\log\)の方程式を解くためには次のような式変形も必要になります。
$$\log_{a}MN=\log_{a}M+\log_{a}N$$
$$\log_{a}\frac{M}{N}=\log_{a}M-\log_{a}N$$
$$\log_{a}M^N=N\log_{a}M$$
$$\log_{a}M=\frac{\log_{b}M}{\log_{b}a}$$
しっかりと頭に入れておきましょう。
log方程式の解き方(1)
次の方程式を解け。
$$\log_{2}(x-1)=3$$
手順は以下の通りです。
真数条件を調べる。
真数や底の部分に文字がある場合には、それぞれの条件出しておきます。
今回は真数部分に\((x-1)\)という文字があります。
この\((x-1)\)は必ず正にならないといけないから。
$$x-1>0$$
$$x>1$$
となるはずだ!という真数条件を出しておきます。
両辺を同じ底を持つ\(\log\)の形に変形
真数条件を出したら、方程式を式変形していきます。
両辺が同じ底を持つ\(\log\)の形になるよう変形していきます。
$$\log_{2}(x-1)=3$$
$$\log_{2}(x-1)=\log_{2}2^3$$
真数同士をイコールで取る。
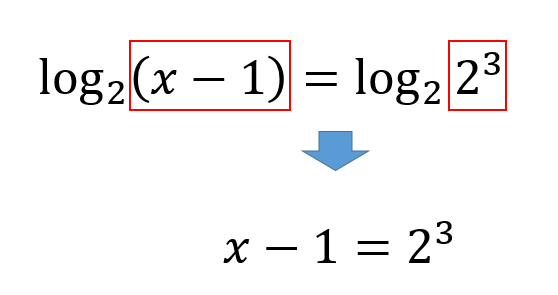
両辺がそれぞれ同じ底を持つ\(\log\)の形にできたら、このように真数同士をとってイコールでつないでやりましょう。
方程式を解く。
あとは、この方程式を解いていくだけです。
$$x-1=2^3$$
$$x-1=8$$
$$x=9$$
真数条件に当てはまるか確かめる。
\(x=9\)と値が求まりましたが、これが真数条件に当てはまるか確かめます。
真数条件は、\(x>1\)でしたね。
そして、答えとして出てきた\(x=9\)は、この条件の中に…
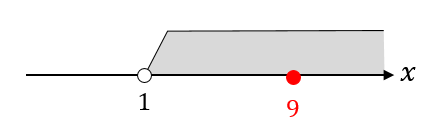
ちゃんと入っているからOKということが分かりますね!
よって、この方程式の解は
$$x=9$$
ということが分かりました!
対数方程式の解き方手順まとめ
- 真数条件を調べる
- \(\log_{□}〇=\log_{□}△\)の形に変形する
- 真数部分をイコールで取って、\(〇=△\)とする
- 方程式を解いて、真数条件に当てはまるか確かめる
方程式の解き方はこんな感じ!
それでは、いろんなパターンの方程式を見ていきましょう。
対数方程式の解き方解説(2)
次の方程式を解け。
$$2\log_{3}(x-3)=\log_{3}x+\log_{3}4$$
まずは真数条件を調べておきましょう。
$$x-3>0 かつ x>0$$
つまり
$$x>3 かつ x>0$$
となるので、それぞれの共通範囲を取ると真数条件は
$$x>3$$
となります。
次に両辺をそれぞれ変形し\(\log_{3}〇=\log_{3}△\)といった形にしていきましょう。
$$2\log_{3}(x-3)=\log_{3}x+\log_{3}4$$
$$\log_{3}(x-3)^2=\log_{3}4x$$
形を揃えることができたので、真数同士をイコールで取りましょう。
$$(x-3)^2=4x$$
$$x^2-6x+9=4x$$
$$x^2-10x+9=0$$
$$(x-9)(x-1)=0$$
$$x=9,1$$
\(x\)の値が求まったので、これらが真数条件に当てはまるかどうかを確かめていきます。
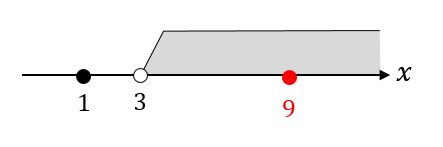
すると、このように1はダメ、9はOKということが分かります。
よって、この方程式の解は
$$x=9$$
ということになります。
対数方程式の解き方解説(3)
次の方程式を解け
$$\log_{3}(x-2)+\log_{3}(x-3)=2\log_{9}(x+1)$$
まずは真数条件を出しておきましょう。
$$x-2>0 かつ x-3>0 かつ x+1>0$$
つまり
$$x>2 かつ x>3 かつ x>-1$$
だから、これらの共通範囲を取ると真数条件は
$$x>3$$
となります。
次に両辺をまとめて\(\log_{□}〇=\log_{□}△\)の形を作っていきます。
しかし、よく見ると…底が揃っていませんね。
まずは、底を揃えることから始めましょう。
底が9になっているものを3に変換します。
$$\log_{3}(x-2)+\log_{3}(x-3)=2\frac{\log_{3}(x+1)}{\log_{3}9}$$
$$\log_{3}(x-2)+\log_{3}(x-3)=2\frac{\log_{3}(x+1)}{2}$$
$$\log_{3}(x-2)+\log_{3}(x-3)=\log_{3}(x+1)$$
これで底が揃いました!
あとは、それぞれまとめていきましょう。
$$\log_{3}(x-2)(x-3)=\log_{3}(x+1)$$
$$(x-2)(x-3)=x+1$$
$$x^2-5x+6=x+1$$
$$x^2-6x+5=0$$
$$(x-5)(x-1)=0$$
$$x=5,1$$
それぞれの値が真数条件に入るか確かめましょう。
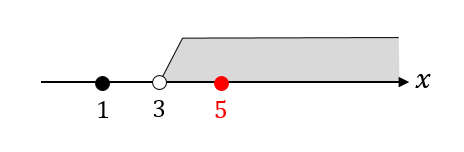
すると、1はダメ、5はOKということが分かりますね。
よって、この方程式の解は
$$x=5$$
となりました。
対数方程式の解き方解説(4)
次の方程式を解け
$$(\log_{3}x)^2+\log_{3}x^2=15$$
まずは真数条件を出しておきましょう。
$$x>0 かつ x^2>0$$
よって、これらをまとめると真数条件は
$$x>0$$
となります。
この方程式においては、\((\log_{3}x)^2\)があることによって\(\log_{□}〇=\log_{□}△\)の形に変形することができませんね…
というわけで
\(\log_{3}x=t\)と置いて、置き換えを利用していきましょう。
すると、方程式は次のように変形し解くことができます。
$$(\log_{3}x)^2+\log_{3}x^2=15$$
$$(\log_{3}x)^2+2\log_{3}x=15$$
$$t^2+2t=15$$
$$t^2+2t-15=0$$
$$(t+5)(t-3)=0$$
$$t=-5, 3$$
ここで\(t\)の置き換えを元に戻し、\(x\)の値を求めていきます。
\(t=-5\)のとき
$$\log_{3}x=-5$$
$$x=3^{-5}$$
$$x=\frac{1}{243}$$
\(t=3\)のとき
$$\log_{3}x=3$$
$$x=3^3$$
$$x=27$$
これらの値は、それぞれ真数条件に入っていますね。
よって、方程式の解は
$$x=\frac{1}{243}, 27$$
となります。
今回の方程式のように\((\log_{3}x)^2\)が出てくれば置き換えのサインですね!
対数方程式 まとめ
お疲れ様でした!
対数方程式の解き方は手順通りやっていければ簡単ですね。
真数条件を出す。
\(\log_{□}〇=\log_{□}△\)の形を作る。
方程式の解が真数条件を満たすか確かめる。
この3ステップで解いていくことができます。
しかし、(4)の問題のように置き換えが必要になるパターンも出てくるので、たくさん問題を解いて解法パターンを身につけていきましょう(/・ω・)/
















コメントを残す