今回は、「年齢算」と呼ばれる問題の解き方について解説していきます。
年齢算とは次のような問題のことだね。
【年齢算の問題】
現在、父は34歳、子どもは4歳です。父の年齢が子どもの年齢の4倍になるのは何年後か求めてみましょう。
中学で学習する方程式を利用すれば簡単に解けたりするんだけど…
ここでは、小学生の方に向けて、どのように考え解いていけば良いのかを解説していきますね!
ポイントは…
年齢の差、比を考える
【年齢算】小学生問題の解き方は?比や線分図を使って考えてみよう!
【年齢算の問題】
現在、父は34歳、子どもは4歳です。父の年齢が子どもの年齢の4倍になるのは何年後か求めてみましょう。
それでは、こちらの問題を考えてみましょう。
父と子どもの年齢差は30歳です。
この年齢差って、何年経っても変わらないものですよね。
だって、父も子どもも毎年同じように歳を重ねていきますから。
このことを頭に入れておいて
問題にあるように、父の年齢が子どもの年齢の4倍になったときの状況を考えてみましょう。
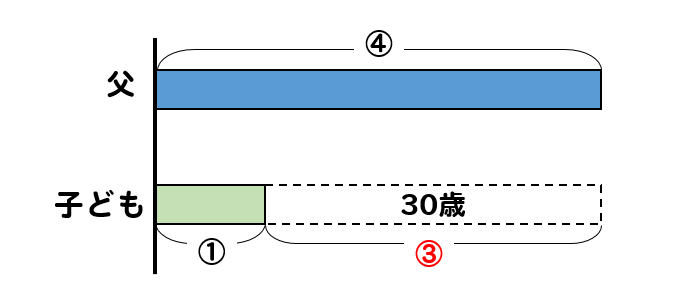
すると、このようなイメージになります。
父は子どもの4倍だから④、子どもは①とすると、年齢差にあたる部分は④-①=③となります。
つまり!
子どもの年齢と年齢差の部分に注目すると
$$(子どもの年齢):(年齢差)=1:3$$
という比の式を作ることができます。
$$(子どもの年齢):30=1:3$$
$$(子どもの年齢)=10歳$$
よって、子どもが10歳になったときに父は子どもの年齢の4倍になることが分かりました。
子どもは現在4歳だから、答えは6年後ということになります。
答え
6年後
これが年齢算の考え方、解き方です。
お互いの年齢差を求める。
年齢差と年齢がどのような比になっているかを考えて解く!
ということです。
練習問題で理解を深めよう!
【年齢算の問題】
現在、父は39歳、子どもは11歳です。父の年齢が子どもの年齢の5倍であったのは何年前か求めてみましょう。
年齢算の例題を解いてみよう①
【年齢算の例題】
父と子どもの現在の年齢の比は10:3です。10年後の2人の年齢の合計が72歳であるとき、父の現在の年齢を求めてみましょう。
現在に比べて10年後
父、子ども2人とも10歳ずつ歳を重ねます。
ということは、現在においての2人の年齢の合計は
$$72-10\times 2=52歳$$
となります。

父の年齢と全体の年齢を比べると
$$(父の年齢):52=10:13$$
$$(父の年齢)=40歳$$
答え
40歳
年齢算の例題を解いてみよう②
【年齢算の例題】
父の年齢は39歳、2人の子どもの年齢は11歳と8歳です。2人の子どもの年齢の和が父の年齢と等しくなったとき、父の年齢は何歳か求めてみましょう。
現時点において、父と2人の子どもの年齢差は
$$39-(11+8)=20歳$$
あります。
1年経つと、父は1歳増えますが2人の子どもの合計は2歳増えます。
このことから、1年経つにつれて父と2人の子どもの年齢差は1歳ずつ縮まっていきます。
つまり、20歳分の差が縮まるまでに
$$20\div 1=20年$$
ということが分かりました。
よって、そのときの父の年齢は
$$39+20=59歳$$
となります。
答え
59歳
年齢算の考え方、解き方まとめ!
お疲れ様でした!
年齢算では、お互いの年齢差を考えること。
問題で指定された〇倍などから、互いの年齢の比を考えること。
これらの考え方を身につけることができれば楽勝ですね(^^)
あとは、いろんな問題を解いて理解を深めていきましょう!

















年齢算の最初の例の問題が2回かいてありますが、一回目の子供の年齢が14歳、二回目の子供の年齢が4歳。正の整数解があるのは二回目のみで、恐らく一回目が誤植だと思います。
↓一回目
【年齢算の問題】
現在、父は34歳、子どもは14歳です。父の年齢が子どもの年齢の4倍になるのは何年後か求めてみましょう。
ご指摘ありがとうございます。
訂正しておきました!
まったく気が付きませんでした(^^;)
難しいけど分かりました
お疲れ様でした^^
ちゃんと理解してもらえたようで嬉しいです!