今回は中1で学習する
『文字式』の単元の中から
マッチ棒の規則性問題について解説していきます。
マッチ棒の問題といえば
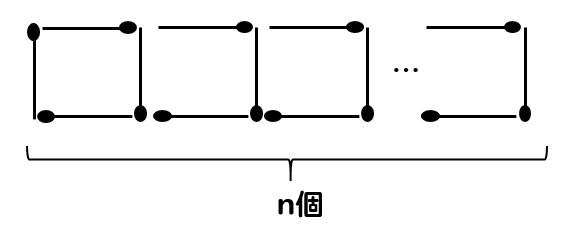
正方形をn番目までつくる場合
マッチ棒は何本必要か?
こんなやつですね。
n番目?

文字が出てくると難しく感じる人も多いようなので
マッチ棒の問題のコツを伝授していきます!
このコツを身につけたら、マッチ棒は楽勝です。
では、いきましょー!
マッチ棒問題のポイント
規則性の問題では
増え方のきまりを見つけることが重要です。
ズバリ!ポイントは
軸と増える本数を見つけること!
例えば、先ほどの正方形の問題では
このように考えてやるといいです。

軸となるマッチ棒が1本あって
正方形が1つ増えるごとにマッチ棒は3本ずつ増えていきます。
つまり、正方形を3個作りたい場合
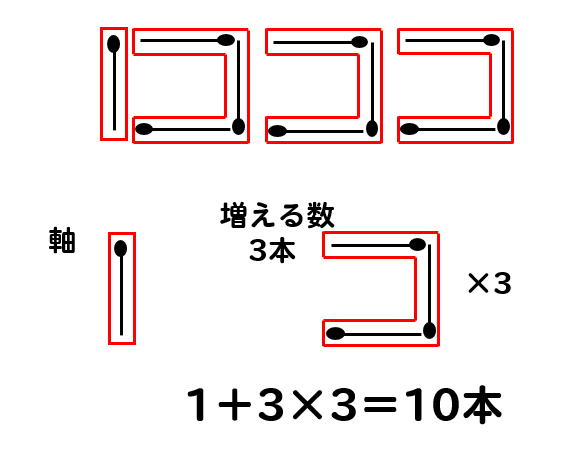
軸が1本あって、それに3本が3回追加されたと考えます。
すると式は
$$1+3×3=10本$$
と計算ができますね。
この考え方を使えば
正方形を100個作る場合といわれても
$$1+3×100=301本$$
と、簡単に計算ができますね。
よって、正方形をn個作るとき
このように文字で聞かれても
$$1+3×n=1+3n本$$
と表してやることができます。
以上のことから、マッチ棒の本数を求めるときのポイントをまとめておきます。
1+(増える数)×(図形の個数)
それでは、このポイントを利用して
いろいろな図形の場合をやってみましょう。
三角形の場合
マッチ棒で三角形を作る場合、マッチ棒の本数はどうなるでしょうか。
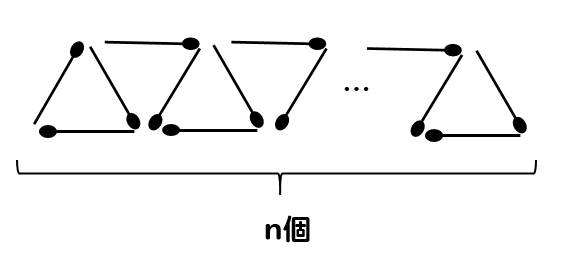
まずは、軸と増える本数を見つけていきましょう。

このように、軸と増える数が分かれば簡単です!
三角形を5個つくるとき、必要なマッチ棒の本数は
$$1+2×5=11本$$
こんな感じで簡単に計算ができますね。
三角形をn個つくるときも同様に
$$1+2×n=1+2n 本$$
と表してやることができます。
六角形の場合
図形の形が変わってもやることは同じです。
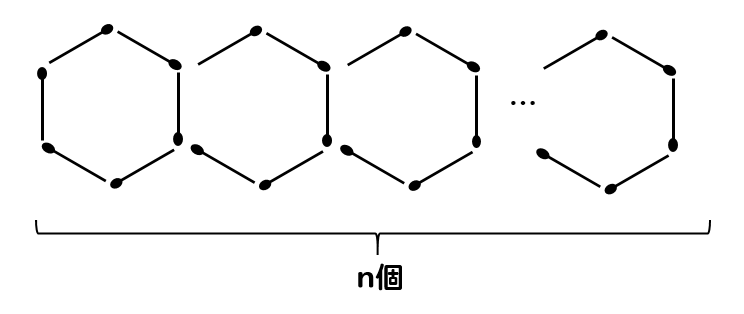
軸と増える数を見つけましょう。

すると、5本ずつマッチ棒が増えていくことがわかるので
六角形を7個つくるとき、必要なマッチ棒の本数は
$$1+5×7=36本$$
六角形をn個つくるとき、必要なマッチ棒の本数は
$$1+5×n=1+5n本$$となります。

ちょっと応用問題
これで図形をn個作ったときのマッチ棒の本数を表すことができるようになりましたね。
すると、次はこんな応用問題が出されることがあります。
マッチ棒を100本使って、以下のように正方形をつくります。
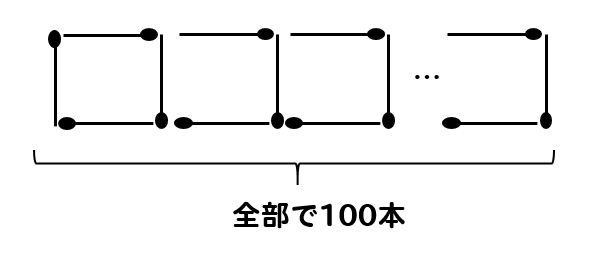
このとき、正方形は全部で何個つくれるか求めなさい。
こういう場合には
正方形がn個作れるとして
このときに必要なマッチ棒の本数を文字を使って表します。
$$1+3×n=1+3n$$
これが100本になるということから
$$1+3n=100$$という方程式を作って計算していきます。
$$1+3n=100$$
$$3n=99$$
$$n=33$$
これで、マッチ棒100本では33個の正方形が作れることがわかりました。
このようにちょっとした応用問題がでてきても
n番目の本数を表すことができれば大丈夫そうですね!
マッチ棒の規則性問題 まとめ
マッチ棒で図形をつくる問題では
軸と増える本数を見つけること!
これがポイントでしたね。
増える本数が分かれば
1+(増える数)×(図形の個数)
この式に当てはめればOKです!
マッチ棒の問題は
見た目は難しそうですが
ポイントさえ覚えておけば楽勝ですね!
ファイトだー!
文字式の文章題を完全マスターしたい方は
>【文字式】数量の表し方、関係を表す式、単位の変換問題などを解説!
こちらのまとめ記事をご参考ください。
マッチ棒の規則性問題を解説!←今回の記事


















コメントを残す