【相似の利用】木の高さを求める方法を問題解説！

今回は、中3で学習する

『相似な図形』の利用問題

木の高さを求める方法について解説していきます。

 

今回の解説には、相似の基本的な性質を利用していきます。

ちょっと不安な方は、上の記事を参考にしてみてくださいね！

 

では、木の高さ求めていきましょー！

木の高さを求める問題とは

相似な図形の単元では、このように木の高さを求める利用問題が出題されます。

 

難しそうに見える問題ですが

実は、相似の基本性質だけ知っておけば解けちゃう

楽勝問題なのです！

難しいと思って、解くの諦めてた！

っていう人は、この記事でしっかりと解けるようになりましょうね(^^)

 

それでは、解法の手順を見ていきましょう。

手順①　相似な三角形を作る

まずは、木の高さをxmとして

図のように三角形を2つ作ってやりましょう。

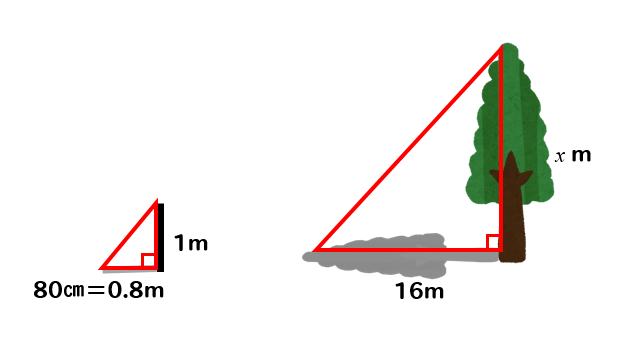
（80㎝は単位を揃えるために、0.8mとします）

するとこの2つの三角形は相似な図形になっているんですね。

 

手順②　対応する辺の長さの比をとる

ここで、相似な図形の基本性質

『対応する辺の長さの比は、すべて等しい』

これを利用します。

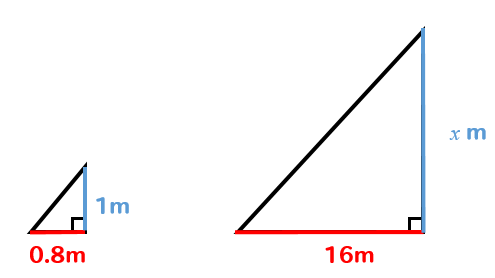
対応する辺の長さの比をとると

$$0.8:16=1:x$$

$$0.8x=16$$

小数が出てきちゃったので、両辺を10倍して計算しやすくします。

$$8x=160$$

$$x=20$$

よって、木の高さは20mと求めることができます。

 

木の高さを求める問題では

1. 相似な三角形をつくる
2. 対応する辺の長さの比から高さを求める

以上！

 

たったの、コレだけです！

とっても簡単ですね(^^)

 

次は、ちょっと応用の問題も見ておきましょう。

 

【応用】見上げる問題とは

木の高さを求める問題で

ちょっとひねってこのような出題のされ方もします。

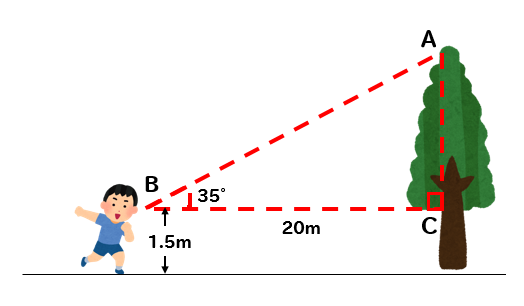
縮図？目の高さ？？

ちょっと何言ってるか分かりにくいですね(^^;

 

手順①　縮図を書く

まずは、問題文にある縮図を書きましょう。

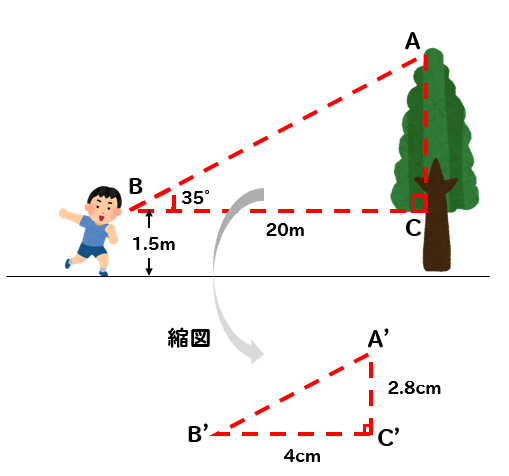
手順②　辺の長さの比をとって、ACの長さを求める

縮図が書けたら、それぞれの三角形の辺の長さの比をとって

ACの長さを求めていきます。

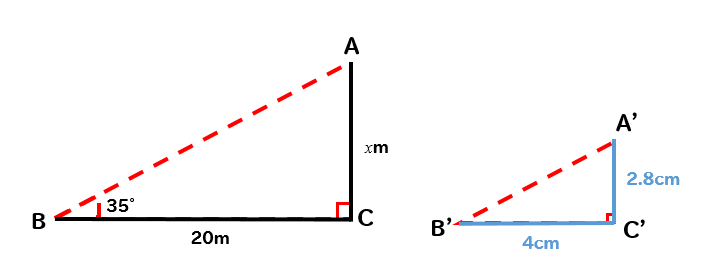
△ABCのBC：ACの比と

△A’B’C’のB’C’：A’C’の比は等しくなるので

$$BC：AC=B’C’：A’C’$$

$$20:x=4:2.8$$

$$4x=56$$

$$x=14$$

$$AC=14cm$$

これでACの長さが求めれましたね。

 

手順③　目の高さを加える

ACの長さを求めることができましたが

これで終わりではありませんよね？

求められているのは、木の高さです。

今、求めることができたのは

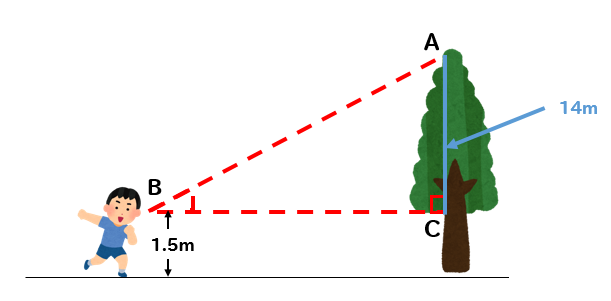
ここの部分です。

 

でも、求めたいのは

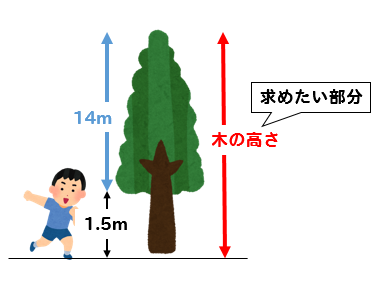
ここの部分。

 

 

だから、ACの長さに目の高さ1.5mを加えてあげて

木の高さは15.5mとなります。

 

 

相似な三角形を作って

辺の長さの比をとるっていう部分では全く同じなのですが

目の高さを加えてあげるっていう部分が少し応用ですね。

 

ん？

目の高さを加えるだけなら

全然応用じゃなくない？

そう思えたあなたは、だいぶ力がついてきている証拠ですね(^^)

木の高さを求める問題 まとめ

木の高さを求めるためには

相似な三角形を作って、辺の長さを比べる

以上！

これだけです。

 

覚えておくのも

『対応する辺の長さの比はすべて等しい』

これだけですね。

 

相似の利用問題ではありますが

難易度は低い楽勝問題なので

絶対に解けるようにしておこうね！

ファイトだー！！