今回の記事では「点と点の距離」を求める方法
その公式の使い方について解説していきます。
点と点の距離とは

こんな感じで、点と点を最短になるよう結んだ線分の長さのことだね!
それではやっていこう(/・ω・)/
点と点の距離を求める公式【1次元】
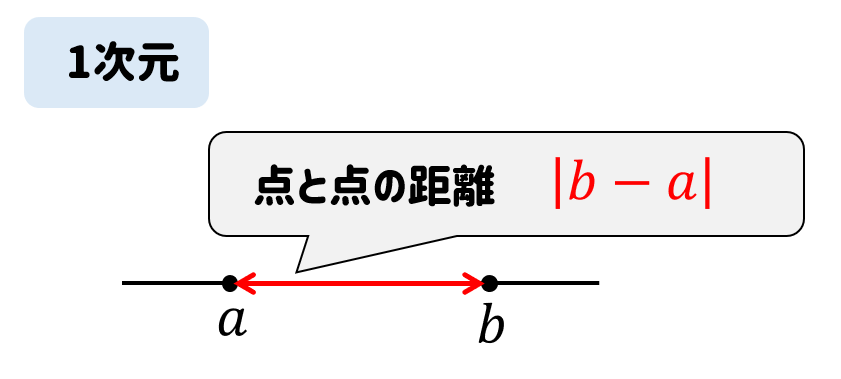
一次元の場合はとっても簡単!
それぞれの差の絶対値を考えればOKです。
もうちょっとシンプルに考えると
(大きい値)ー(小さい値)
と考えておけば良いです、
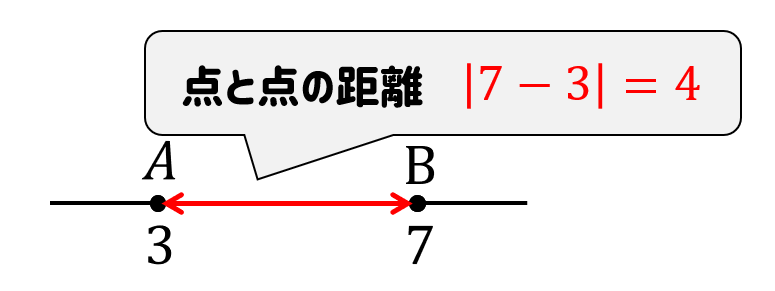
【例題】
2点A\((3)\)、B\((7)\)の距離を求めなさい。

それでは、公式に当てはめて考えてみましょう。
$$AB=|7-3|=|4|=4$$
となります。
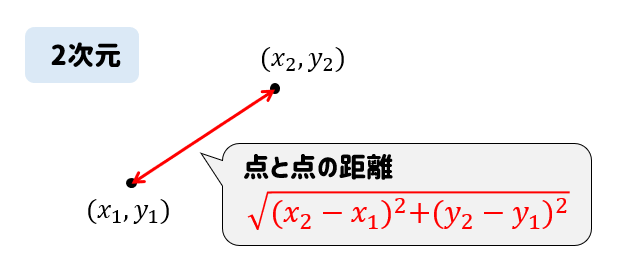
点と点の距離を求める公式【2次元】
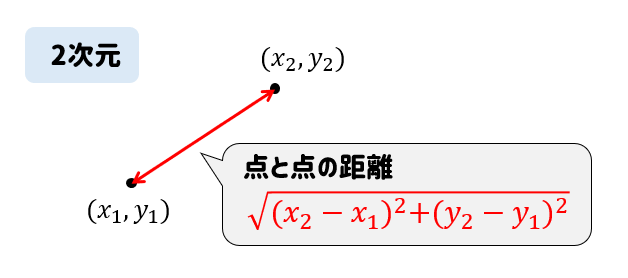
2次元の場合、公式だけ見てしまうと難しそうに感じます。
だけど、実際の計算はとってもシンプルです!
具体例を見ながら計算手順を確認しましょう。
【例題】
2点A\((1,3)\)、B\((4,7)\)の距離を求めなさい。
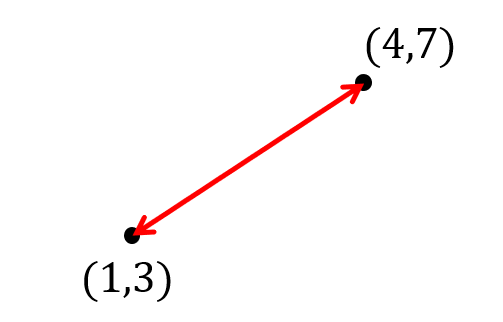
それでは、公式に当てはめて計算していきましょう。
まずは、それぞれの点の\(x\)座標を引いて二乗!
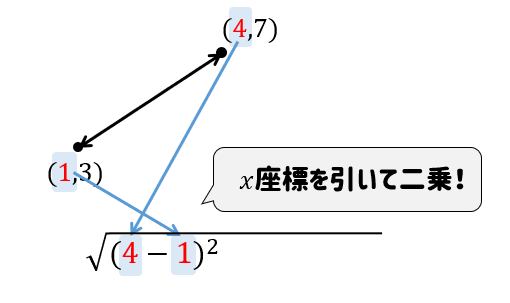
次に、\(y\)座標を引いて二乗!
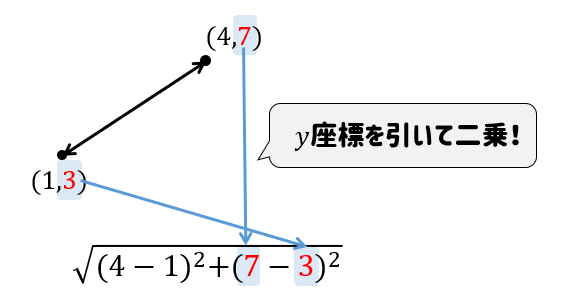
このとき、座標を引く順番はどちらからでもOK
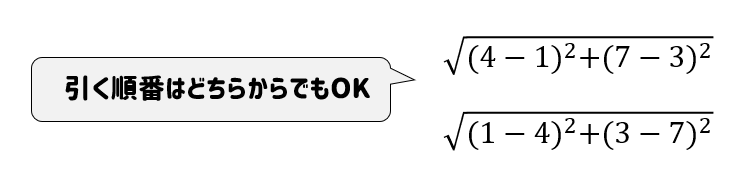
結局、2乗してしまうので同じ値になってしまいます。
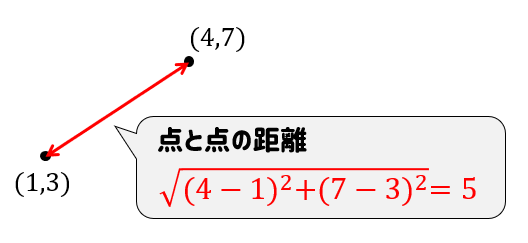
最後に計算をすれば、2点の距離が求まります。
$$\begin{eqnarray} \sqrt{(4-1)^2+(7-3)^2}&=&\sqrt{3^2+4^2}\\[5pt]&=&\sqrt{9+16}\\[5pt]&=&\sqrt{25}&=&5\end{eqnarray}$$
とっても簡単だね(^^)
なぜこのような公式で求めることができるのか疑問に思った方は
こちらの記事内で公式の意味を解説しているので確認してみてください。
三平方の定理が分かれば簡単に理解できますよ(/・ω・)/
点と点の距離を求める公式【3次元】

3次元の場合、座標が3つになるだけで
計算の手順などは2次元の場合と全く同じです。
ちょっと計算の手間がかかるというくらいですね。
では、具体例を見ておきましょう。
【例題】
2点A\((1,2,4)\)、B\((2,1,6)\)の距離を求めなさい。
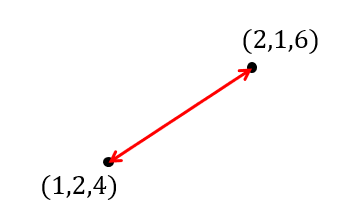
$$\begin{eqnarray} \sqrt{(2-1)^2+(1-2)^2+(6-4)^2}&=&\sqrt{1^2+(-1)^2+2^2}\\[5pt]&=&\sqrt{1+1+4}\\[5pt]&=&\sqrt{6}\end{eqnarray}$$

3次元だからといって、特別な計算をするわけではありませんね。
2次元の公式にひと手間加わっただけです。
空間の中で三平方の定理を使っただけにすぎません(^^)
点と点の距離を求める【練習問題】
それでは、練習問題で理解を深めておきましょう。
【練習問題】
2点A\((3)\)、B\((-5)\)の距離を求めなさい。
【練習問題】
2点A\((-1.2)\)、B\((-3.8)\)の距離を求めなさい。
【練習問題】
2点A\((2,-5)\)、B\((4,-2)\)の距離を求めなさい。
【練習問題】
2点A\((4,-5)\)、B\((3,1)\)の距離を求めなさい。
【練習問題】
2点A\((-2,-1,3)\)、B\((0,3,-1)\)の距離を求めなさい。
まとめ!
お疲れ様でした!
それでは、最後に点と点の距離を求める公式を確認しておきましょう。


点と点の距離を求めることができるようになれば、次は点と直線だ!
>【点と直線の距離】公式の覚え方と使い方をイチから解説するぞ!
















コメントを残す