今回は、高校数学Ⅱで学習する「ω(オメガ)を使った計算」について解説していきます。
ωってなに!?
顔文字に使うやつでしょ??
ってイメージだと思いますが、テストにも出題される大切な問題になるので、しっかりと理解しておきましょう。
今回の記事で解説するのは次のような問題だ!
\(x^3=1\) の虚数解の1つを\(\omega\)とするとき、次の式の値を求めなさい。
(1)\(\omega^6+\omega^3+1\)
(2)\(\omega^{10}+\omega^5+1\)
(3)\(\displaystyle{\omega^4+\frac{1}{\omega^4}}\)
では、これらの計算をやるためのポイントを解説していきます。
こちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
ωの計算のポイント!
ωの計算をやるためにおさえておきたいポイントが2つ!
- \(\omega^3=1\)
- \(\omega^2+\omega+1=0\)
この2つのポイントを使いながらωの計算をやっていきます。
①\(\omega^3=1\) というのは簡単なので覚えやすいですね。
だけど、②\(\omega^2+\omega+1=0\) はちょっとだけ複雑だね(^^;)
でも、ちゃんと意味を理解しておけば簡単に導くことができます。
このように変形することができれば
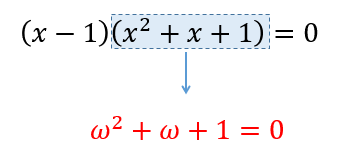
ここの部分だな!ってことで導くことができますね。
もしも、ωの②の式を忘れてしまった場合には、このように式変形して思い出していってください。
では、これらのポイントを使いながらωの計算をやってみましょう。
ωの計算のやり方解説!
ωの問題(1)の解説
\(x^3=1\) の虚数解の1つを\(\omega\)とするとき、次の式の値を求めなさい。
(1)\(\omega^6+\omega^3+1\)
ωの計算は、式の中に\(\omega^3\) を見つけて、1に変えてやるというのがポイントです。
$$\omega^6=\omega^3\times \omega^3=1\times 1=1$$
であることを利用すると次のようになります。
$$\begin{eqnarray}\omega^6+\omega^3+1&=&(\omega^3)^2+\omega^3+1\\[5pt]&=&1^2+1+1\\[5pt]&=&3 \end{eqnarray}$$
答え
$$3$$
ωの問題(2)の解説
\(x^3=1\) の虚数解の1つを\(\omega\)とするとき、次の式の値を求めなさい。
(2)\(\omega^{10}+\omega^5+1\)
まずは、式の中に\(\omega^3\)を見つけて、1に変換しましょう。
$$\begin{eqnarray}\omega^{10}+\omega^5+1&=&(\omega^3)^3\cdot \omega +(\omega^3)\cdot \omega^2+1\\[5pt]&=&1^3\cdot \omega +1\cdot \omega^2+1\\[5pt]&=&\omega +\omega^2+1 \end{eqnarray}$$
これ以上、\(\omega^3\) がないなぁーってところまで変形ができたら
ωのポイント②\(\omega^2+\omega+1=0\) より
$$\begin{eqnarray}&\omega +\omega^2+1=0 \end{eqnarray}$$
ってことが分かりましたね(^^)
まずは、\(\omega^3\) を見つけて、1に変換する。
その後は、ポイント②を使って変形する。
この手順で解いていけばOKです。
答え
$$0$$
ωの問題(3)の解説
\(x^3=1\) の虚数解の1つを\(\omega\)とするとき、次の式の値を求めなさい。
(3)\(\displaystyle{\omega^4+\frac{1}{\omega^4}}\)
分数になっているので、難しそうに見えますが…大丈夫!
やり方はシンプルです♪
今まで通り、\(\omega^3\) を見つけて、1に変換しましょう。
$$\begin{eqnarray}\omega^4+\frac{1}{\omega^4}&=&(\omega^3)\cdot \omega +\frac{1}{\omega^3 \cdot \omega}\\[5pt]&=&\omega +\frac{1}{\omega} \end{eqnarray}$$
ここからの変形が…ん?となってしまいがちなのですが
分数の分母、分子に\(\omega^2\)を掛けることで無理やり\(\omega^3\) の形を作りましょう。
$$\omega +\frac{1}{\omega}=\omega +\frac{\omega^2}{\omega\cdot \omega^2}=\omega +\frac{\omega^2}{\omega^3}$$
すると、\(\omega^2+\omega+1=0\) を変形して \(\omega^2+\omega=-1\) となることを利用して次のように計算を進めていくことができます。
$$\begin{eqnarray}\omega +\frac{\omega^2}{\omega^3}=\omega+\omega^2=-1\end{eqnarray}$$
答え
$$-1$$
ωの計算のやり方まとめ!
お疲れさまでした!
ωの計算をやっていくためには、2つのポイントをおさえておく必要があります。
- \(\omega^3=1\)
- \(\omega^2+\omega+1=0\)
まずは、①のポイントを使って1に変換しましょう。
次に②を使ってさらに変換する!
分数が出てきた場合には、分母と分子にωを掛けて無理やり3乗の形を作るというパターンもあるので頭に入れておきましょう。
以上だ(/・ω・)/
















わかりやすかったです!助かりました!ありがとうございました!