「三角錐の体積・表面積がわからん！」
「とにかく求め方をサクッと知りたい！」
という方に向けて、今回の記事では三角錐の計算について3分で理解できるようにまとめています。
この記事を読みながら手元の宿題やワークを一緒に解き進めていきましょう。
三角錐の体積
次の三角錐の体積を求めなさい。
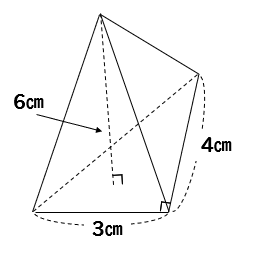
三角錐の体積を求めるときに気をつけたいのは、必ず\(\frac{1}{3}\)を掛けることです。
四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。
また、底面の三角形の面積は、\((底面)\times (高さ)\times \frac{1}{2}\)となることもおさえておきましょう。
すると、計算は次のようになります。
〇 三角錐の体積は、底面積を求めて高さをかける、そして\(\times \frac{1}{3}\)を忘れないように！
三角錐の表面積
三角錐の表面積を問われることは少ないようですが、難しい話ではないのでサクッと解説しておきますね。
まずは三角錐の展開図がどんなものか確認しておきましょう。
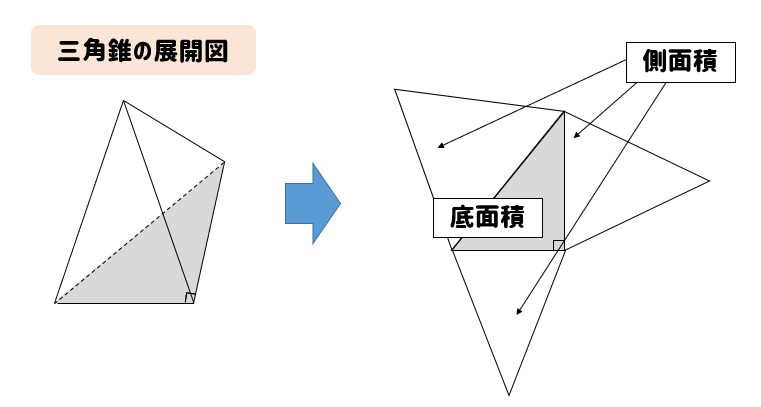
底面の三角形に対して、側面の三角形が3つ分くっついている形になります。
つまり、四角錐の表面積とは次のように求めることができます。
では、実際に問題を解いてみましょう。
次の三角錐の表面積を求めなさい。
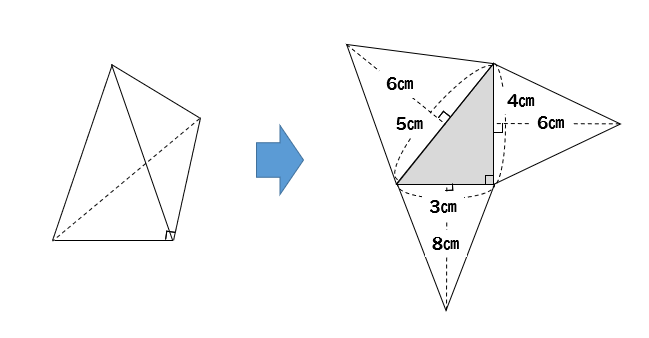
※長さはテキトーに決めましたので、図形的にあり得ない大きさになっているかもしれません(^^;)あくまで計算方法を紹介するための例題です。
展開図のイメージがつくれたら、あとはそれぞれを計算するだけです。
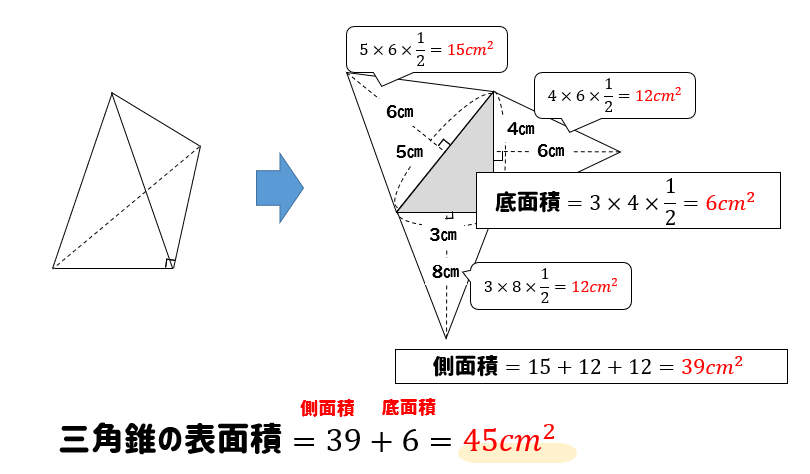
〇 三角錐の表面積は底面と側面（三角形3つ分）をあわせたもの。
〇 展開図を書いて、それぞれを計算して合計していきましょう。
まとめ！
お疲れ様でした！
お手元の宿題、ワークの問題は解けましたか？
反復練習を通して、理解を深めておきましょうね(/・ω・)/
成績を上げて、志望校合格を勝ち取りたい中3生の方！
数スタの無料メルマガ講座で合格を勝ち取りませんか？
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ わからないを解決！質問対応サポート
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
コメントを残す