今回の記事では、高校入試で出題されるような
「規則性の問題」
について、いろんな問題を取り上げて解説していきます。
規則性の問題って、苦手に感じてる人が多いよね(^^;)
そんな嫌われものの規則性と仲良くするためには…
やっぱりたくさん問題を解いて、相手を知ることが大事!
ってなわけで
いくつか問題をピックアップしてみたので挑戦してみましょう!
今回の記事は、こちらの教材の一部を抜粋して作成しています。

こちらの教材を利用することで、
みんなが知らない規則性の公式が学べて、
入試本番ではスラスラ解けるようになりますよ。
とにかく合格したい!
という方は、ぜひこちらの教材をご利用くださいね!
マッチ棒の規則性
【問題】
次の図のように、マッチ棒を使って正方形を左から右へ順につくっていく。
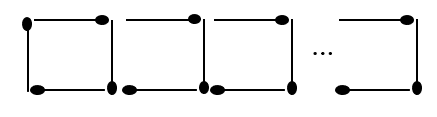
(1)正方形を5個つくるにはマッチ棒が何本必要か。
(2)正方形を\(n\)個つくるのに必要なマッチ棒の本数を\(n\)を使った式で表しなさい。
(3)100本のマッチ棒を使うと、いくつの正方形がつくれるか。
正方形を1つ増やすごとに、マッチ棒が何本ずつ増えていくかに注目しましょう。
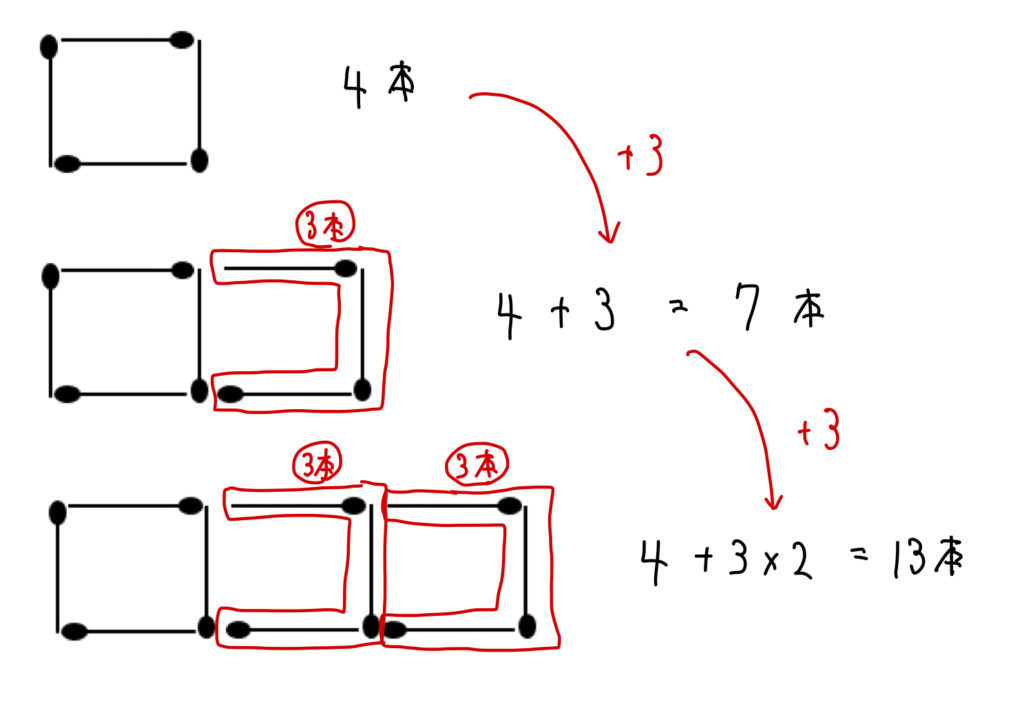
今回であれば、このように3本ずつ増えていることがわかります。
正方形2個であれば、3本。
正方形3個であれば、3本が2回分。
正方形5個であれば、3本が4回分加えられるはずです。
ってことで、正方形を5個つくるときには
$$4+3\times 4=16本\cdots(解)$$
となります。
では、正方形を\(n\)個つくるときには?
という話になるのですが、考え方は同じです。
正方形\(n\)個であれば、3本が\((n-1)\)回分加えられるはずですから
$$4+3(n-1)=(3n+1)本\cdots(解)$$
となります。
最後に、100本のマッチ棒を使ってできる正方形の数を考えます。
これは(2)で求めた\(n\)の式を用いると簡単に解けます。
$$\begin{eqnarray}3n+1&=&100\\[5pt]3n&=&99\\[5pt]n&=&33 \end{eqnarray}$$
よって、33個が答えとなります。
答え
(1)\(16\)本
(2)\((3n+1)\)本
(3)\(33\)個
今回の問題のように、
同じ数だけ増えたり、減ったりする数列を考える場合
次のように、\(n\)の式を表すことができます。
$$(最初の数)+(n-1)\times (増加する数)$$
今回の問題であれば、
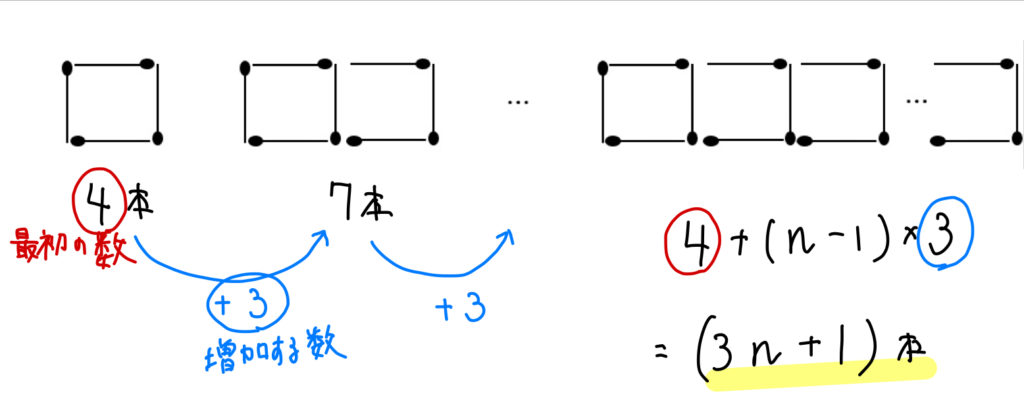
こんな感じで考えることができますね(^^)
これを覚えておくと、規則性の問題では非常に役立ちます。
この公式をもっと詳しく学びたい場合は、
図形が変化していく規則性
【問題】
碁石を使って、次の図のように碁石の数を増やして正方形を2つ合わせた図形をつくっていきます。
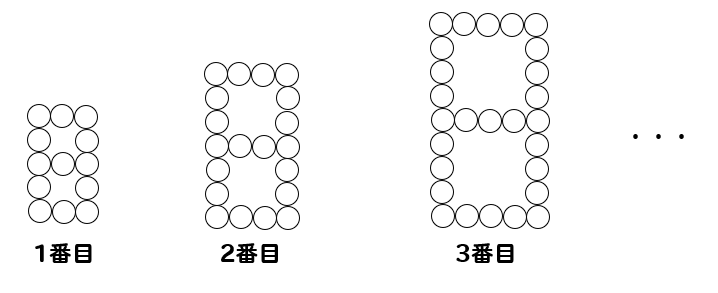
(1)5番目の図形には、碁石が何個必要か。
(2)\(n\)番目の図形には、碁石が何個必要か\(n\)の式で表せ。
今回の問題のように、図形が変化していく場合には
どの部分が増えていっているのかに注目してください。
この問題であれば、
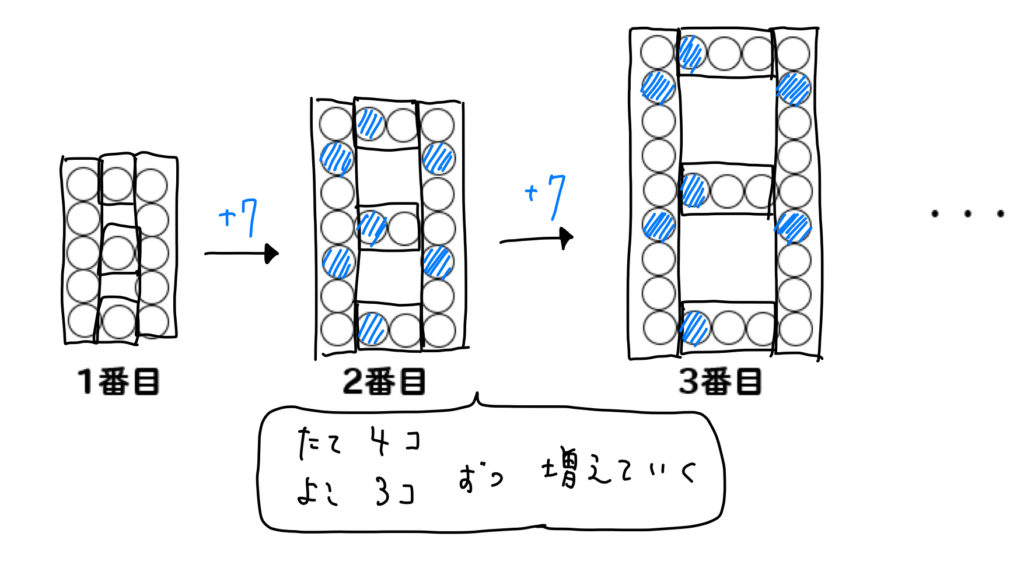
ここの部分に注目できればいいですね!
すると、碁石は7個ずつ増えているってことがわかります。
パッと見では分かりにくいですが
変化する前と後をよく見比べて
どこが増えているのか、その数は何個か?
ということに注目していきましょう。
すると、5番目の碁石の数は、
最初の数が13個で、そこから7個が4回分加わっているはずなので
$$13+7\times 4=41個\cdots (解)$$
となります。
となると、\(n\)番目の碁石の数も同様に、
最初の数が13個で、そこから7個が\((n-1)\)回分加わっているはずなので
$$13+(n-1)\times 7=(7n+6)個\cdots(解)$$
となります。
答え
(1)\(41\)個
(2)\((7n+6)\)個
【問題】
下の図のように、1辺1㎝の正方形を並べて、1番目、2番目、3番目…と図形を作っていく。
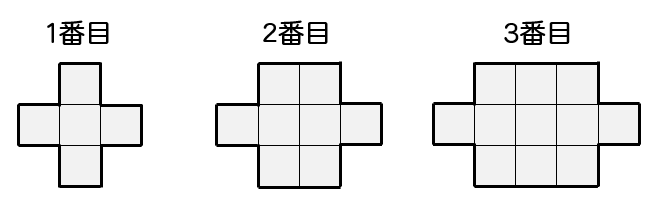
(1)8番目の図形には、何個の正方形が必要か。
(2)図の太線は図形の周の長さを表している。\(n\)番目の図形の周の長さは何㎝になるか、\(n\)を用いて表しなさい。
今回の問題では、
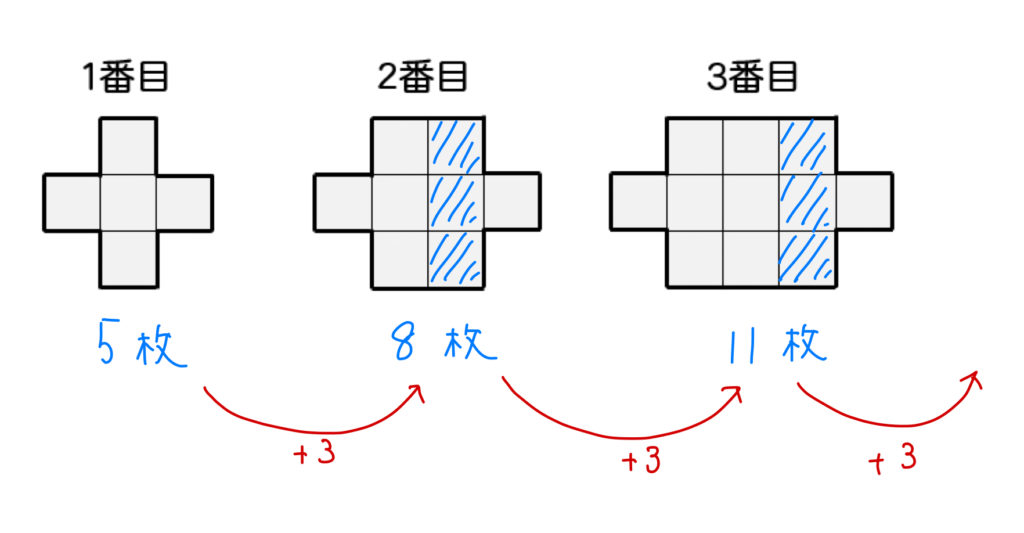
このように正方形が3つずつ増えていることが分かりますね。
ってことは、8番目のときには
$$5+3\times (8-1)=5+21=26個\cdots(解)$$
となります。
次に周の長さですが、前の図形と比較すると
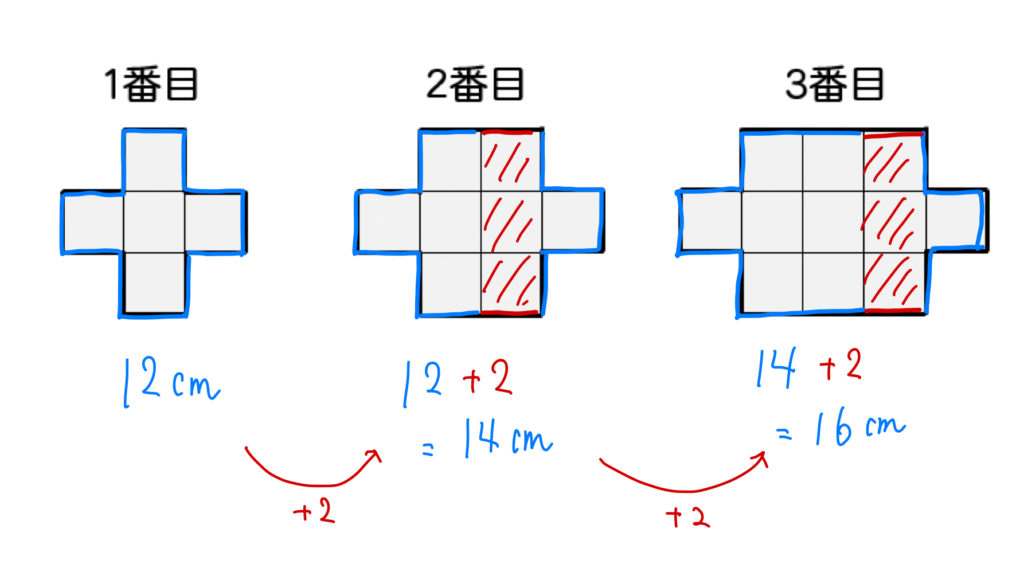
このように赤くなっている部分(2㎝)が増えていっていることが分かりますね。
よって、\(n\)番目のときには
$$12+2\times(n-1)=(2n+10)cm\cdots(解)$$
となります。
答え
(1)\(26\)個
(2)\((2n+10)\)cm
和を考えていく規則性
【問題】
次の図のように碁石を増やしていく。
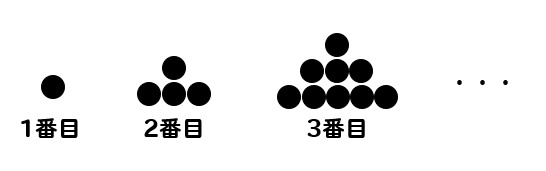
(1)5番目の碁石の個数は全部で何個になるか。
(2)10番目の碁石の個数は全部で何個になるか。
(3)\(n\)番目の碁石の個数を\(n\)を用いて文字で表しなさい。
今回の問題では、次のように考えていくとよいです。
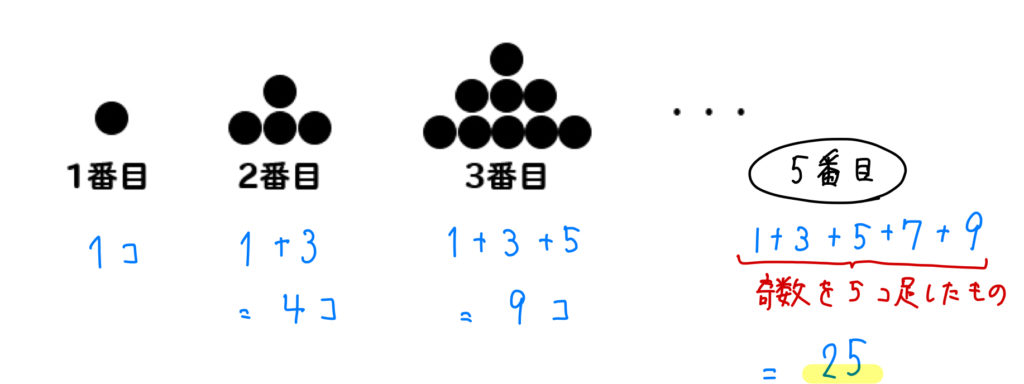
奇数の数だけ増えていくということが読み取れるので、
5番目のところの式は、
$$1+3+5+7+9=25\cdots(解)$$
このように、5番目までの奇数を足した値となります。
まぁ、5番目を求めるくらいであれば
そこまで難しい計算ではないので、頑張って計算していけばよいです。
ですが、10番目を求めなさい。と言われれば
$$1+3+5+\cdots$$
式が長すぎて、計算がめんどいですね(^^;)
なので、等差数列の和を求めるのに
覚えておくとちょっと便利な公式についてご紹介します。
※等差数列とは、同じ数だけ増えたり減ったりする数の並びのこと。
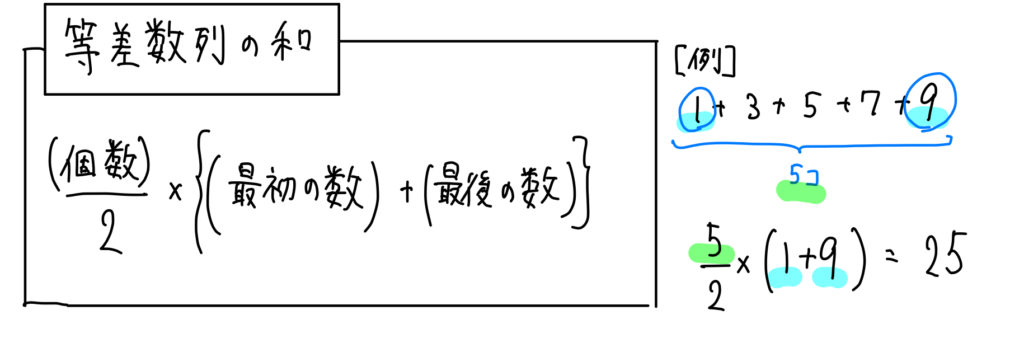
この公式に当てはめて考えると、
数の最初と最後、そして個数だけが分かっていれば
簡単に和を求めることができるようになります。
では、こちらの公式を使って10番目の碁石の個数を求めましょう。
10番目の奇数は、\(2\times 10-1=19\)になることから
\( 1+3+5+\cdots+19 \) の値を求めればよいので、公式に当てはめると
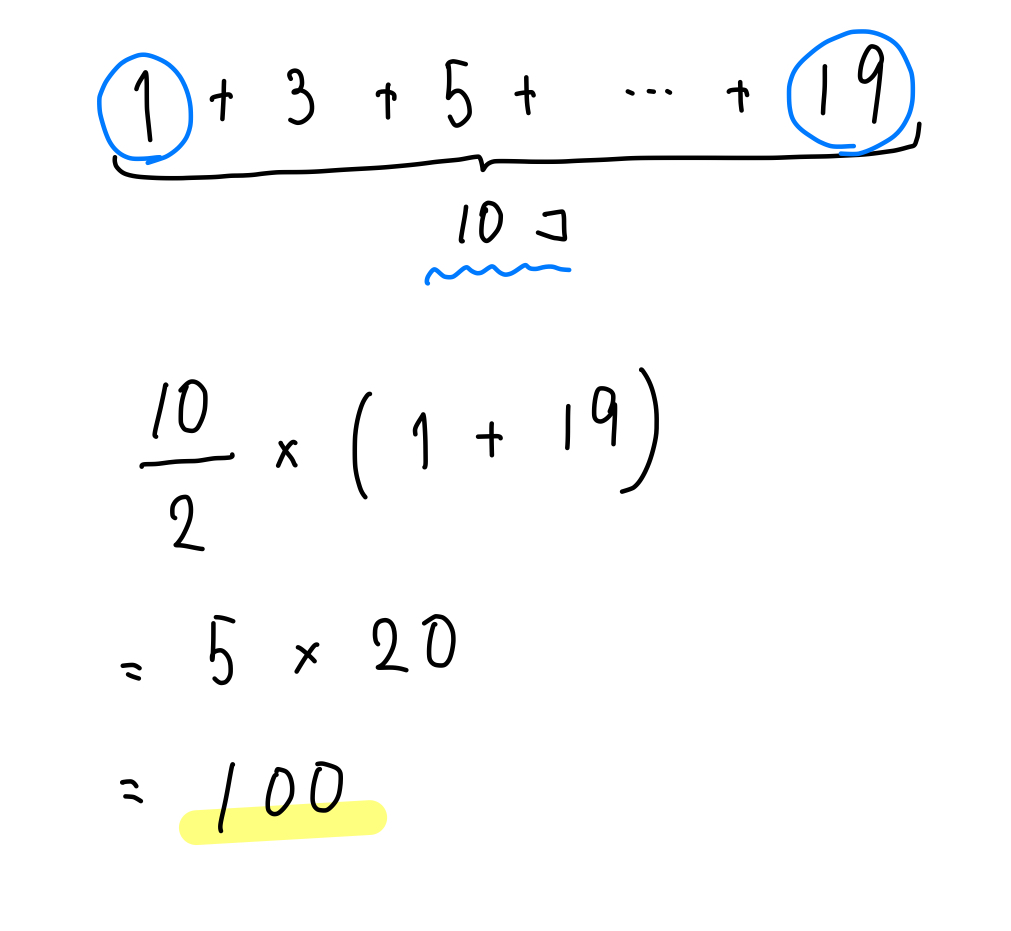
よって、答えは100個…(解) となります。
公式を覚えておくと便利だよね(^^)
では、\(n\)番目のときにはどうなるか考えてみましょう。
\(n\)番目のときは次のような計算で求めることができます。
$$1+3+5+\cdots+(2n-1)$$
これを先ほどの公式に当てはめてみると
$$\begin{eqnarray}\frac{n}{2}\{1+(2n-1)\}&=&\frac{n}{2}\times 2n\\[5pt]&=&n^2 \end{eqnarray}$$
となりました。
答え
(1)\(25\)個
(2)\(100\)個
(3)\(n^2\)個
〇段目の数は?の規則性
下の図のように、ある規則に従って自然数が書いてあるカードを並べる。
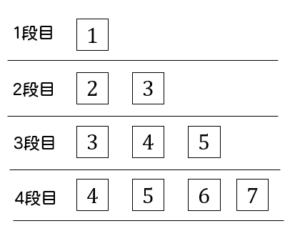
(1)7段目の一番右に置かれた数は何か。
(2)\(n\)段目の一番右に置かれた数を\(n\)を使った式で表せ。
(3)31の数がはじめて出てくるのは何段目か。
7段目の数は、7から始まり7個分だけ数が並べられるはずです。
つまり、7段目は
$$7,8,9,10,11,12,13$$
と書き並べてみると、すぐに答えは分かりますね。
よって、7段目の一番右の数は\(13\)となります。
数えれる場合には、全て書き出してみると良いですが
数が大きくなってきた場合には大変ですよね(^^;)
なので、こういった見方もできるようにしておきましょう。
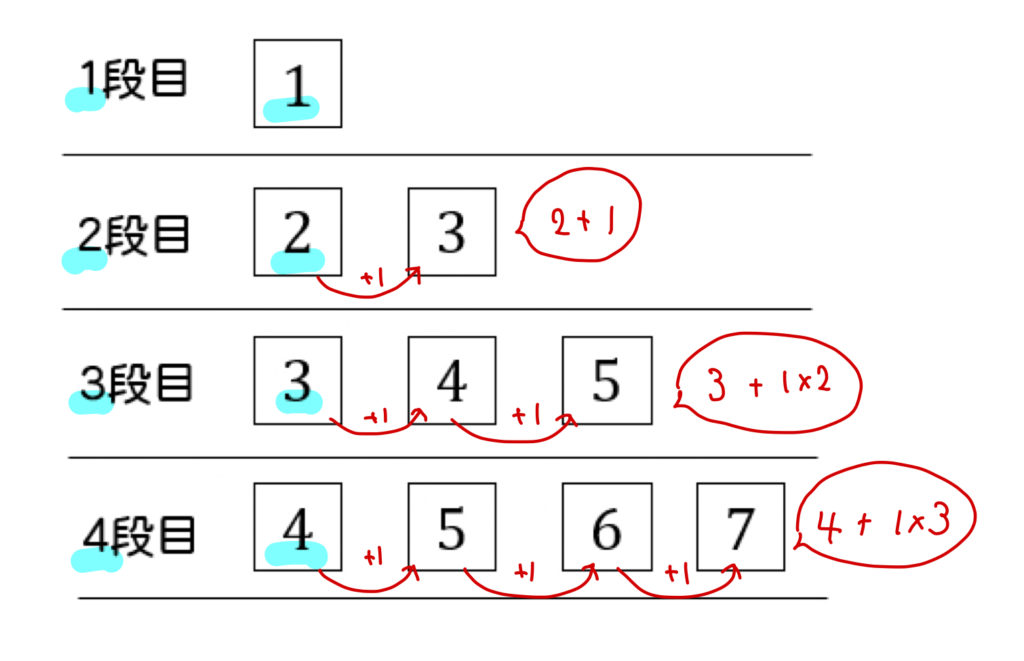
〇段目と同じ数からスタートしていて、
1を\((〇-1)\)回分足した値が一番右の数となっています。
こういった見方ができていれば、
\(n\)段目の場合も簡単にできますね(^^)
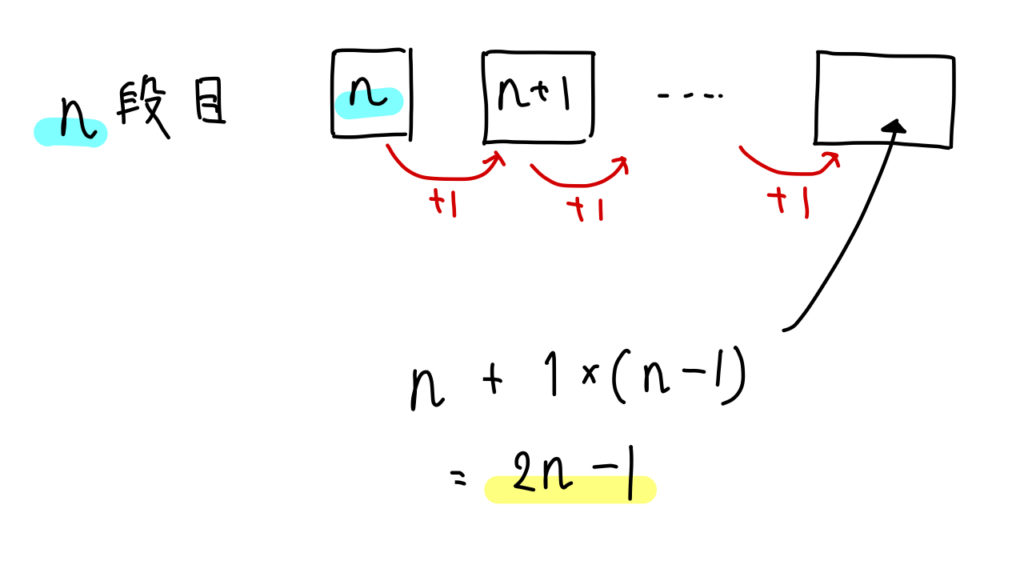
このように考えて、\(n\)段目の一番右の数は、\(2n-1\)と表せました。
では、初めて31が出てくるのが何段目なのかを考えていきましょう。
今回の問題では、初めて出てくる数は、
まずは、一番右に置かれることになります。
なので、先ほど求めた\(n\)段目の一番右の数\(2n-1\)を用いていきます。
$$\begin{eqnarray}2n-1&=&31\\[5pt]2n&=&32\\[5pt]n&=&16\end{eqnarray}$$
よって、31が初めてでてくるのは16段目となりました。
答え
(1)\(13\)
(2)\(2n-1\)
(3)\(16\)段目
まとめ!
お疲れ様でした!
規則性の問題を考えるためには、
等差数列の知識を覚えておくと便利です。
$$n番目=(最初の数)+(n-1)\times (増加する数)$$
$$等差数列の和=\frac{個数}{2}\{(最初の数)+(最後の数)\}$$
この公式を使いこなせるよう
たくさんの問題に挑戦してみてくださいね(^^)
規則性をゼロから+10点するための教材

模試の度に、
「今回は規則性が出ないといいな…」
と願い続けるのはやめにしましょう。
規則性の問題は、
コツをつかんでしまえば、
誰でも簡単に解くことができるようになります。
むしろ、コツを習得した人にとって規則性の問題は、
他のどんな単元よりも簡単に感じるはずですよ。
教材を利用した方は、
どんどん「できる、わかる」を実感していってます(^^)
《利用者さんの声》
分かりやすい言葉で説明されているので、
長い解説を読むのが苦手な我が子にとっては、
とても使いやすいと思います。
レベル別に段階をおって進めるのも良いと思います。
何より、公式をまず覚えさせ問題を解かせるというのは目からウロコでした。
教材の詳細はこちらからどうぞ!

















https://study-line.com/kokonyushi-kisokusei/
〇段目の数は?の規則性
答えの記載 (2)2n+1
2n−1 が正しいとおもます. 誤記でしょうか?
訂正しておきましたm(__)m
ご指摘ありがとうございました!
わかりやすかったです!
お役に立てたようで嬉しいです^^
わかりやすい
ありがとうございます!!
とってもわかりやすかったです。規則性苦手なので助かります。
お疲れ様でした!
規則性はコツを掴んでしまえば楽勝です^^
頑張ってくださいね!
本当にわかりやすかったです!
過去問だけでは不安だったのでうれしいです。
それはよかった!
試験がんばってね!
すごすぎ!
規則性苦手だったのに、めっちゃ分かりやすい!
説明が丁寧で、すごくありがたいです!!
試験で規則性が出てこないことを願うどころか、
出てきて欲しいくらいになりました!笑
お役に立てて良かったです^^
次のテストで規則性がでてきて
満点がとれることを期待してますよ~(‘ω’)ノ
分かりやすかったです。実践してみます。
ありがとうございます^^
ぜひ実践してみてください!
勉強したで簡単だった
とってもわかりやすくて良かった!
スマホで手軽に見れるし、解説も理解しやすい!
受験期でぜんぜんとけなかったけどこの問題解いて、少しできるようになっててよかった!本当にありがとうございます!
お役に立ててよかったです!
これを機に規則性マスターを目指してくださいね(‘ω’)ノ
わかりやすくて良い!基礎から学べたし、解いてて楽しいと思えた!ありがとうございます!
よかったです^^
規則性って解けると楽しいですよね!
自分はずっと連立方程式を使ってでしか解けてなかったので(本質的に解こうとしてなかったので)ちゃんと理解できました!次から実践しようと思います。
どんどん実践していってください^^
規則性のコツがわかってくると問題を解くのが楽しくなりますよ!
神サイトだ
ありがとうございます!!
すごい
規則性やっと理解できました
とてつもなくわかりやすかったです。
分かりやすいね