【数Ⅱ】定積分を含む関数のやり方をていねいにイチから解説！

高校数学Ⅱで学習する積分の単元から

「定積分を含む関数の求め方」

についてイチから解説していきます。

こんなやつですね！

【問題】

次の等式を満たす関数$f(x)$を求めよ。

$$f(x)=4x+2\int_0^2 f(t) dt$$

これは、すごーく質問が多い問題です。

途中で何をやってるのかが分からなくなりやすいんですよね。

なので、解き方の手順をイチからていねいに解説していきますね！

こちらの動画でも解説しています！

動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾

高校メルマガ講座の無料登録はこちら！

Contents

定積分を含む関数のやり方手順
例題に挑戦！
まとめ！

定積分を含む関数のやり方手順

【問題】

次の等式を満たす関数$f(x)$を求めよ。

$$f(x)=4x+2\int_0^2 f(t) dt$$

まず、関数の中に入っている定積部分$\int_0^2 f(t)dt$は、

上端2、下端0ともに定数だから

$\int_0^2 f(t)dt$の部分も定数になることがわかります。

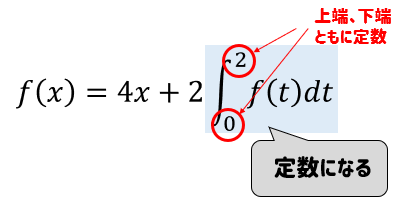
なので、$\int_0^2 f(t)dt=a(定数)$ とおいて考えていきます。

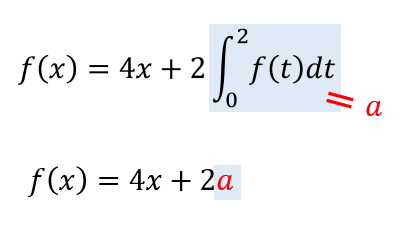
すると、$f(x)$は上のように置き換えることができます。

この$f(x)=4x+2a$を$t$に置き換え、

これを最初に置いた、$\int_0^2 f(t)dt=a$に代入して計算していくと

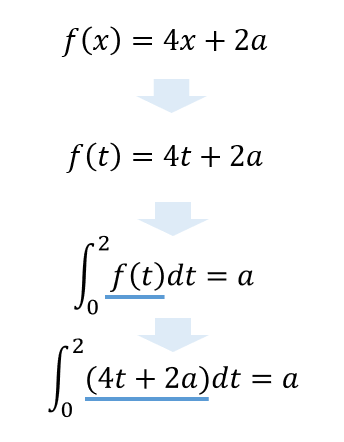
このようになります。

あとはこちらを計算していけば$a$の値が求まります。

$$\begin{eqnarray}\int_0^2 (4t+2a)dt&=&a\\[5pt][2t^2+2at]_0^2&=&a\\[5pt]8+4a&=&a\\[5pt]3a&=&-8\\[5pt]a&=&-\frac{8}{3} \end{eqnarray}$$

$a$の値が求まったので、

$f(x)=4x+2a$に代入すれば完成となります。

$$\begin{eqnarray}f(x)&=&4x+2\times (-\frac{8}{3})\\[5pt]&=&4x-\frac{16}{3}\cdots(解) \end{eqnarray}$$

手順まとめ！

関数の中にある定積分を$a$とする。
$f(x)$を$a$で置き換える。
②の式から$x$を$t$にした式を作る。
③を①の式に代入して、$a$の値を求める。
④を②に代入すれば式の完成！

例題に挑戦！

では、理解を深めるためにいくつか例題を確認しておきましょう。

【問題】

次の等式を満たす関数$f(x)$を求めよ。

$$f(x)=3x^2-4+\int_{-1}^2 xf(t) dt$$

こちらも先ほどと同じように解いていくのですが、

1つ気を付ける点があります。

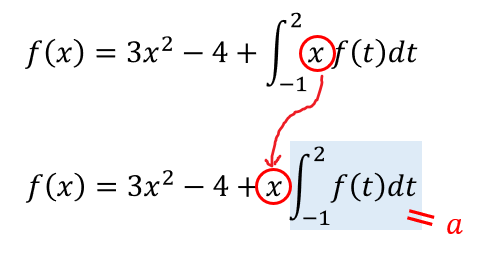
定積分の中に入っている$x$は外に出してから

置き換えをするようにしてください。

ここを乗り越えたら

先ほどとやり方は同じです！

$\int_{-1}^2 f(t)dt=a(定数)$とすると、

$f(x)=3x^2-4+ax$ となります。

よって、$f(t)=3t^2+at-4$ と表せるので

これを $\int_{-1}^2 f(t)dt=a$ に代入すると

$$\begin{eqnarray}\int_{-1}^2 (3t^2+at-4)dt&=&a\\[5pt][t^3+\frac{1}{2}at^2-4t]_{-1}^2&=&a\\[5pt](8+2a-8)-(-1+\frac{1}{2}a+4)&=&a\\[5pt]\frac{3}{2}a-3&=&a\\[5pt]\frac{1}{2}a&=&3\\[5pt]a&=&6 \end{eqnarray}$$

$a=6$ を$f(x)=3x^2-4+ax$に代入したら完成ですね！

$$f(x)=3x^2+6x-4\cdots(解)$$

となります。

【問題】

次の等式を満たす関数$f(x)$を求めよ。

$$f(x)=x\int_0^1 f(t) dt+\int_0^1tf(t)dt+1$$

ふ、2つも定積分が入ってるけど…！？

と、見た目で戸惑ってしまいますね(^^;)

ですが、やることはシンプル！

定積分が2つあるなら、それぞれ違う文字で置いてやればOK。

$\int_0^1 f(t)dt=a$, $\int_0^1 tf(t)dt=b$ とすると

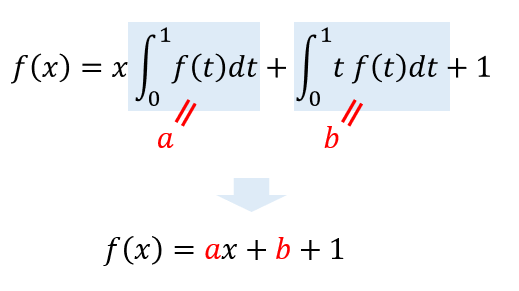
さらに、$f(t)=at+b+1$だから

$\int_0^1 f(t)dt=a$に代入すると

$$\begin{eqnarray}\int_0^1 (at+b+1)dt&=&a\\[5pt][\frac{1}{2}at^2+bt+t]_0^1&=&a\\[5pt]\frac{1}{2}a+b+1&=&a\\[5pt]a+2b+2&=&2a\\[5pt]a-2b&=&2\cdots① \end{eqnarray}$$

$\int_0^1 tf(t)dt=b$に代入すると

$$\begin{eqnarray}\int_0^1 t(at+b+1)dt&=&b\\[5pt][\frac{1}{3}at^3+\frac{1}{2}bt^2+\frac{1}{2}t^2]_0^1&=&b\\[5pt]\frac{1}{3}a+\frac{1}{2}b+\frac{1}{2}&=&b\\[5pt]2a+3b+3&=&6b\\[5pt]2a-3b&=&-3\cdots② \end{eqnarray}$$

このように2本式が作れたら

①②をそれぞれ連立方程式で解いていきましょう。

$$\begin{eqnarray} \left\{ \begin{array}{l} a-2b=2 \\ 2a-3b=-3 \end{array} \right. \end{eqnarray}$$

これを解くと、$a=-12,$ $b=-7$となります。

よって、それぞれの値を$f(x)=ax+b+1$に代入すると

$$f(x)=-12x-6\cdots(解)$$

となります。