比例のグラフから式を求める方法とは？ラクな裏技の考え方とは

今回は比例のグラフから式を求める方法について解説していきます。

 

こちらに書いている内容に目を通しておいてもらえると

今回の記事は理解が早いと思います＾＾

 

比例の式の作り方については、こちらの動画でも解説しています(/・ω・)/

 

比例のグラフから式を求める方法

グラフから式を求める方法には2つのパターンがあります。

まずは一般的なパターンから見ていきましょう。

式に代入するパターン

式に代入するパターンの手順はこうです。

1. グラフが通る座標を読み取る
2. 読み取った座標の値をy=axに代入してaの値を求める。
3. aの値をy=axに代入して完成

 

それでは手順通り、こちらのグラフを式にしてみます。

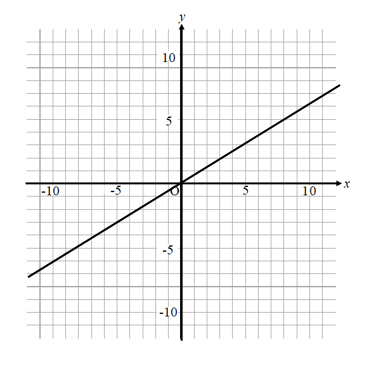
まずは【手順①】 グラフの通る座標を読み取りましょう。

グラフの直線上を見ていって

目盛り上にぴったり重なっているところに点をとっていくと

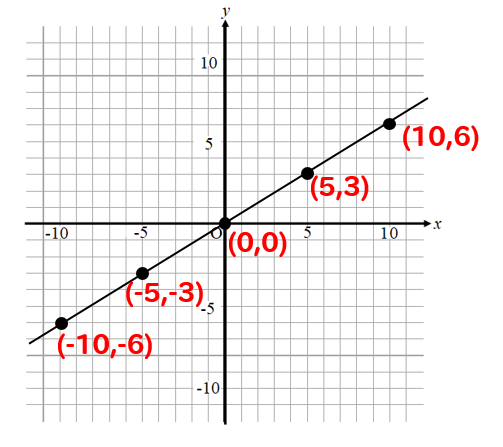
このように座標を読み取ることができます。

これらの中から原点(0,0)以外の点を選びます。

（なるべく数が小さいのを選びましょう）

 

今回は(5,3)という座標を選びます。

これは

『x＝5のときy＝3になる』

ということを表しています。

 

【手順②】 読み取った座標をy=axに代入します。

x＝5のときy＝3を、比例の式であるy＝axに代入してやると

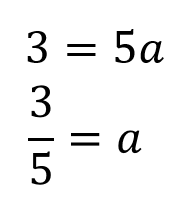
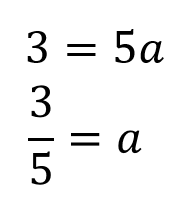
これでaの値(比例定数)が求まりました。

 

最後は【手順③】 aの値をy=axに代入して完成させます。

a=3/5を代入してやると

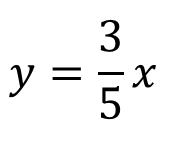
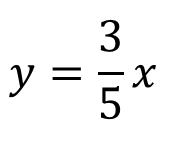
となり、式が完成しました！

 

多くの教科書や参考書に載っているやり方がコレでしょうね。

しっかりと座標を読み取って、式に代入、計算ができれば大丈夫です！

ただし、代入であったり方程式の計算などが必要になる為

文字式の計算や方程式の基礎をしっかりと理解しておく必要があります。

 

 

次はグラフを書くときに利用したあの考え方を使います。

移動を見るパターン

移動を見るパターンの手順はこちらです。

1. グラフが通る座標を見つける
2. どれくらい移動しているかを見て、比例定数aを決める
3. aの値をy=axに代入して完成

 

では、さっきと同じグラフを式にしてみますね。

【手順①】でグラフが通る座標を見つけると

ここまでは、さっきと同じです。

 

【手順②】で、それぞれの座標がどれくらい動いているかを調べます。

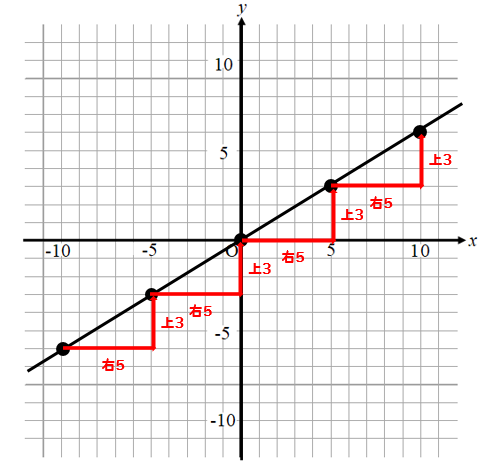
全て右に５、上に３ずつ動いていることが分かりますね。

このように動いている数が確認出来たら、比例定数はこのようになります。

右に動いている数５を分母に

上に動いている数３を分子にとると

比例定数は3/5となりますね。

（下に動いているグラフであれば分子の数をマイナスにしてください）

 

最後は

【手順③】で比例定数をy=axの式に代入してやると

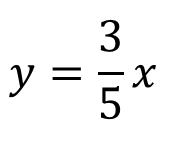
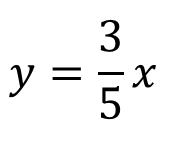
このように式が完成します。

 

ポイントとしては、座標がどれくらい動いているかを見ることで

方程式を解かなくても比例定数を見つけることができるという点ですね。

 

比例定数の作り方は

右に動いている数を分母

上下に動いている数を分子に乗っけるだけです。

 

ちょっと覚えることはありますが、習得してしまえばこっちのほうが楽かもしれませんね！

 

では、この移動を見るパターンを使って

いくつか問題を解いてみましょう。

 

問題演習で確認！

 

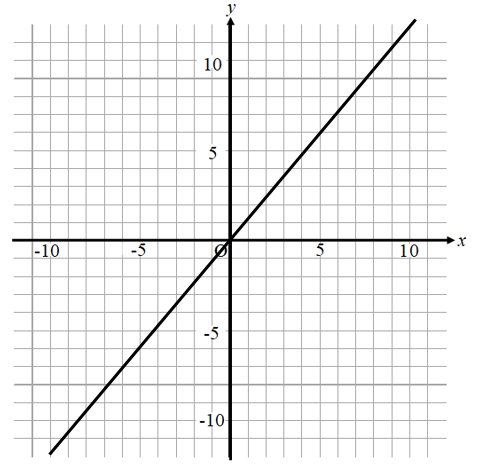
どれくらい動いているか確認してみると

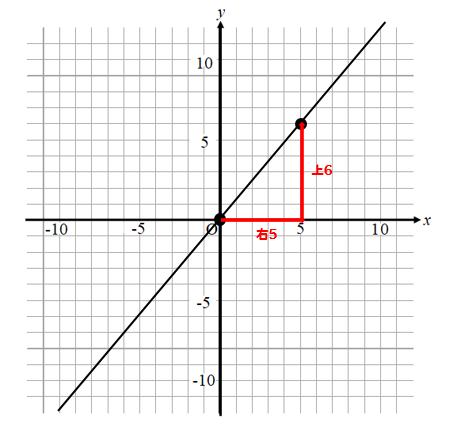
右に５、上に６動いていますね。

よって比例定数は6/5となります。

グラフの式は

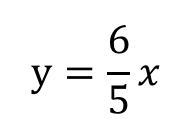
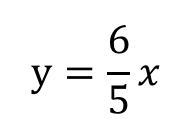
となります。

 

 

 

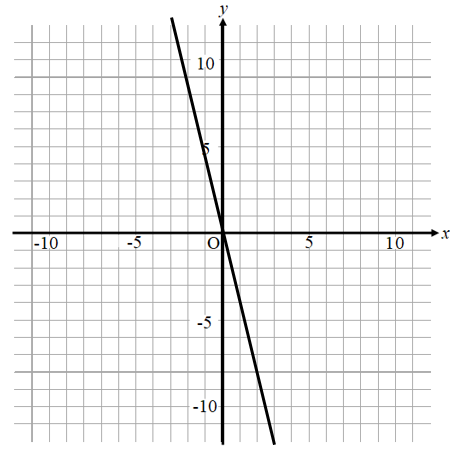
どれくらい動いているか確認してみると

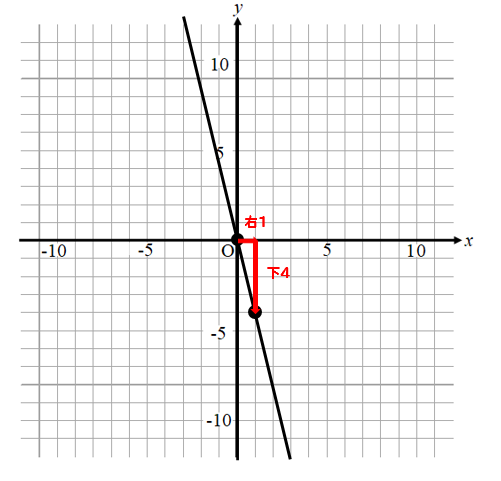
右に１、下に４動いているので

比例定数はー4/1となり、約分ができるのでー4となります。

グラフの式は

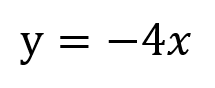
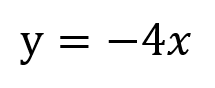
となります。

 

 

移動を見ながら式を作る方法

ご理解いただけましたでしょうか？

 

 

式の作り方は、自分が理解しやすい方を使ってもらえたらOKです。

いろんな問題に挑戦して理解を深めていきましょう！

ファイトだー！！