今回の記事では、次のような反比例の変域に関する問題を解説していきます。
【反比例の変域問題①】
関数\(\displaystyle{y=\frac{18}{x}}\)で、\(x\)の変域を\(2≦x≦6\)とするとき、\(y\)の変域を求めなさい。
【反比例の変域問題②】
\(y\)は\(x\)に反比例し、\(x\)の変域が\(2≦x≦6\)のとき、\(y\)の変域が\(2≦y≦6\)となる。このとき、\(y\)を\(x\)の式で表せ。
変域…何それ!?
不等号…ややこしい!!
っと思って、難しい問題のように思えるんだけど
実は、そんなに難しくない。
むしろラクな問題かもしれません(^^)
というわけで、それぞれの問題について解き方を確認していきましょう。
今回の記事は、こちらの動画でも解説しています(/・ω・)/
【反比例】変域問題の解き方は??問題①の解説!
【反比例の変域問題①】
関数\(\displaystyle{y=\frac{18}{x}}\)で、\(x\)の変域を\(2≦x≦6\)とするとき、\(y\)の変域を求めなさい。
変域の問題っていうと、難しく聞こえちゃうので別の言い方にしておきましょう。
変域とは、範囲のことです!
\(x\)の変域、つまりヨコの範囲を決めると
\(y\)の変域、つまりタテの範囲がどうなるか?
ということを聞いてるってことですね。
まずは、ざっくりでいいので\(\displaystyle{y=\frac{18}{x}}\)のグラフを書きます。
だいたいの形があっていればいいので、点をとって正確に書く必要はありません。
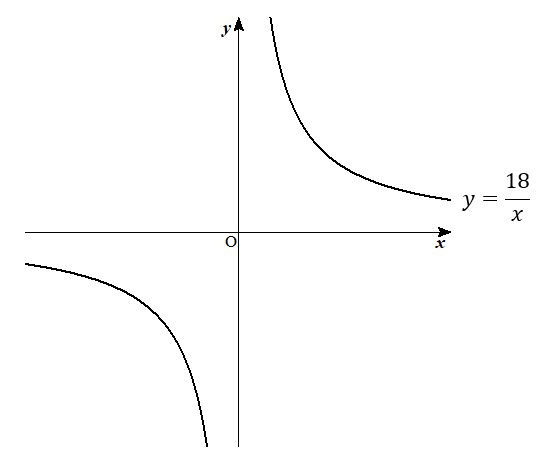
そして、このグラフの\(x\)座標が2から6になっている部分に印をつけて切り取ります。
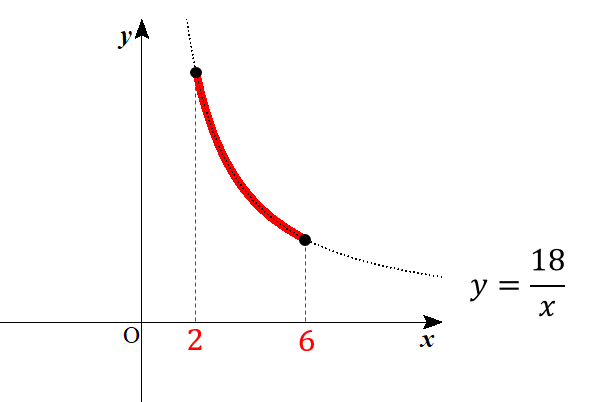
すると、切り取られた部分のタテの範囲を見てみると
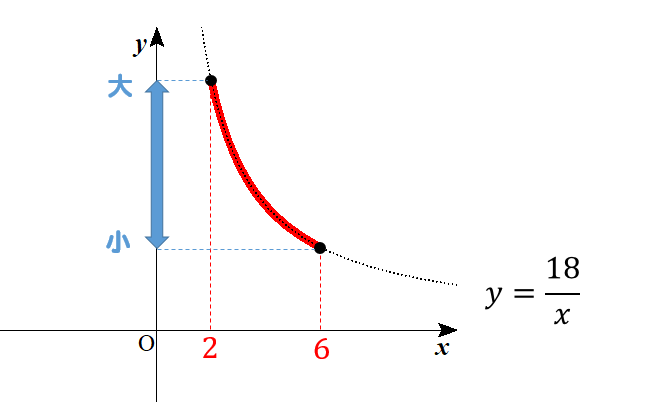
このようになっていますね。
\(x=2\)のところが一番大きくて、\(x=6\)のところが一番小さい。
それぞれの\(y\)座標がどうなっているかは、反比例の式に代入すれば求めれます。
\(x=2\)のとき
$$y=\frac{18}{2}=9$$
\(x=6\)のとき
$$y=\frac{18}{6}=3$$
よって、このようになります。
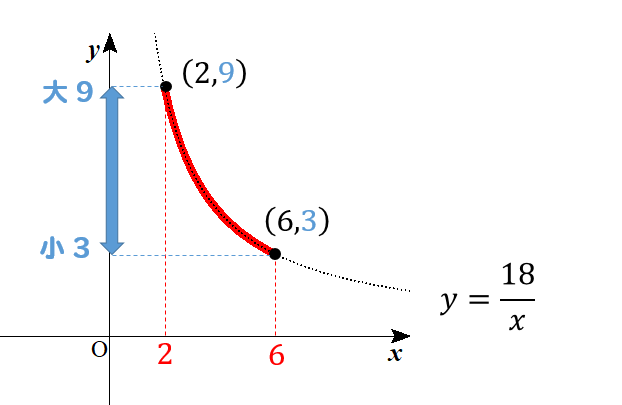
よって、タテの範囲は3から9だということが分かるので
\(y\)の変域は、\(3≦y≦9\) となります。
答え
$$3≦y≦9$$
簡単にグラフを書いて、ヨコの範囲を切り取る。
そして、そのときの座標を読み取ってタテの範囲を求める。
簡単ですね(^^)
慣れてくればグラフは書かなくても、頭の中で理解できるようになってきます。
それは、ひたすら練習を繰り返せば身についてくるので、がんばって反復練習していきましょう!

【反比例】変域問題の解き方は??問題②の解説!
【反比例の変域問題②】
\(y\)は\(x\)に反比例し、\(x\)の変域が\(2≦x≦6\)のとき、\(y\)の変域が\(2≦y≦6\)となる。このとき、\(y\)を\(x\)の式で表せ。
この問題は、範囲をヒントに式を作れというものですね。
まずは、\(x\)と\(y\)の変域から反比例のグラフがどのような形になるのかを読み取ります。
反比例のグラフには、次のような2種類の形があります。
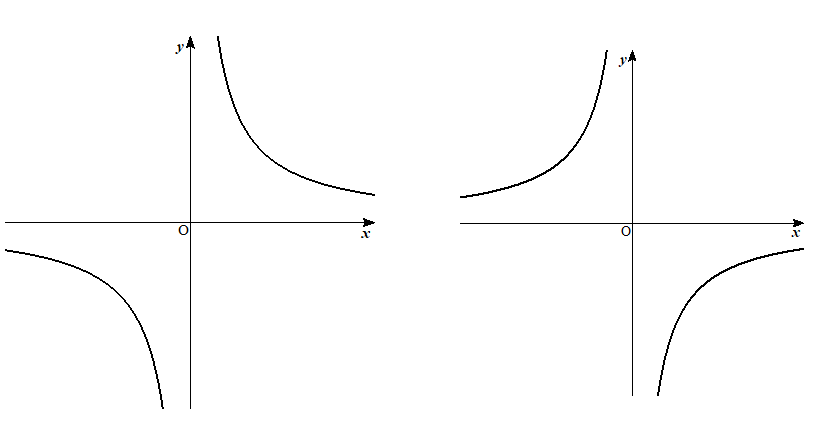
\(x\)の変域が\(2≦x≦6\)のとき、\(y\)の変域が\(2≦y≦6\)となる。
ということから、グラフのヨコを2から6で切り取ると、タテは2から6である正の部分になるから
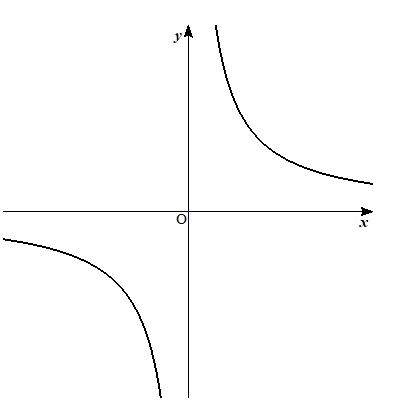
こちらの形であるということが判断できます。
なので、このグラフを利用して変域を書き込みます。
すると、次のように反比例のグラフが通る座標を読み取ることができます。
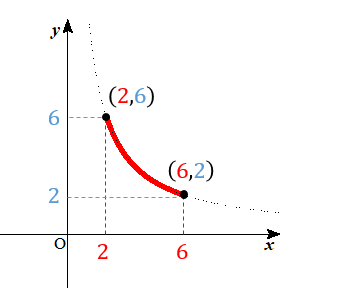
反比例のグラフは、\((2,6)\)、\((6,2)\)を通ることが分かります。
どちらの座標を使ってもいいので、反比例の式\(\displaystyle{y=\frac{a}{x}}\)に代入して比例定数を求めると
$$6=\frac{a}{2}$$
$$12=a$$
よって、反比例の式は
$$\color{red}{y=\frac{12}{x}}$$
となりました。
答え
$$y=\frac{12}{x}$$
今回の問題のように、変域から式を求めたい場合
まずは、グラフがどのような形になるのかを考えることが大事!
グラフの形が決まったら、それを使って座標を読み取ることができます。
座標が分かれば式を作るのは楽勝ですね(^^)
【反比例】変域問題の解き方は??まとめ!
お疲れ様でした!
どちらの問題においても、複雑な計算は一切ありませんでした。
ポイントは、変域を範囲としてとらえ、グラフを切り取るイメージを持つことができるかどうかですね。
変域の問題が苦手だという人は、変域の意味を理解せず何となく解法を覚えてしまっている場合が多いです。
そうではなく、変域とは範囲だ!
ということを理解しておけば、すっごく単純な問題だったりするよね(^^)
問題の解き方が分かったら、あとはたっくさん練習して理解を深めていきましょう。
ファイトだ(/・ω・)/
反比例の変域問題の解き方は??←今回の記事


















すごい