今回は反比例の式の作る(aを求める)方法について解説していくよ!
反比例の式をつくる
というワードだけ聞いてしまうと
すっごい難しい問題のように感じるんだけど
実際には5秒もあれば解けちゃうようなラッキー問題なんだよね
絶対にやり方を覚えて、得点アップにつなげてください!
反比例の式の作り方について、こちらの動画でも解説しています(/・ω・)/
反比例の式の作り方はたったコレだけ!
xの値とyの値を掛けて
上に乗っけるだけで終了!!
例えば
yはxに反比例し、x=2のときy=3である。
こときの、yをxの式で表しなさい。
xの2とyの3を掛けて
比例定数は6
あとは、反比例の式であるy=a/xのxの上に乗っけてやれば
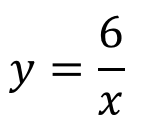
完成です!!
すっごく楽ですね。
掛けてxの上に乗っけるだけ!
なぜxの値とyの値を掛けると比例定数であるaを求めることができるのかと言えば、反比例の性質を覚えておけば理解できますね。
反比例というのは、xの値とyの値を掛けると常に同じ値になる関係であり、その値のことを比例定数と呼ぶんでしたね。
反比例の性質忘れちゃった人はこちらも読んでおきましょう^^
今回の式は正確に表すとこのような変形で求められています。
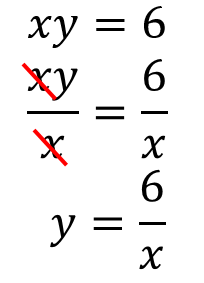
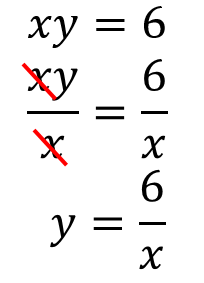
まぁ、途中の変形は面倒なので
比例定数が求まれば、上に乗っけると覚えておけば大丈夫です!
xの値とyの値を掛けると比例定数が求まる。
グラフから式を作る場合も簡単!
グラフから式を作る場合も簡単です!
グラフが通っている座標を、どこでもいいので読み取りましょう。
あとで計算が楽になるよう、なるべく小さな数が出てくる座標が良いです。
このグラフの場合
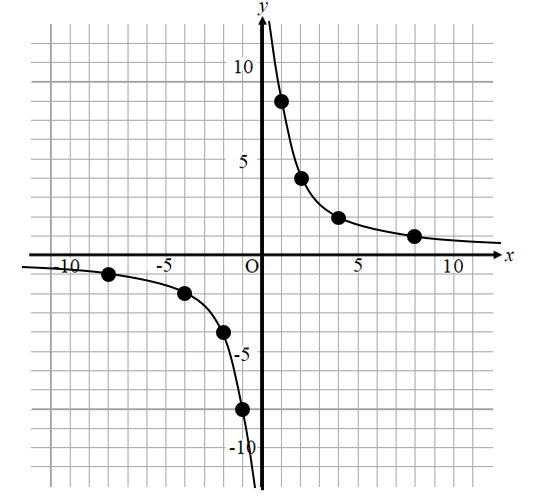

(-8,-1)(-4,-2)(-2,-4)(-1,-8)
(1,8)(2,4)(4,2)(8,1)
という座標が読み取れますね。
今回は(1,8)を使うことにします。
(1,8)はx=1、y=8ということを表しています。
比例定数はxの値とyの値を掛ければ良いのだから
1×8=8(比例定数)
※どの座標を使って計算しても同じ値になります。
比例定数が求まれば
xの上に乗っけてあげて


となります。
簡単ですね♪
では練習問題をやってみて完全習得していきましょう。


練習問題で理解を深める!
問題
yはxに反比例し、対応するx、yの値が次のとき、yをxの式で表しなさい。
(1)x=-3のときy=4である
(2)x=-4のときy=-5である。
(3)x=3のときy=5/3である。
では、解説をサクッといきますね。
とにかくxとyの値を掛けて上に乗っけるだけです!
では(1)の解説
xの値とyの値を掛けると
-3×4=-12
よって


次は(2)の解説!
xの値とyの値を掛けると
-4×(-5)=20
よって
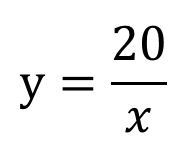
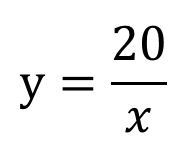
簡単じゃい!
次(3)の解説!
おっと分数…ちょっと怯んでしまいそうですが
これもやり方は一緒!
xの値とyの値を掛けると
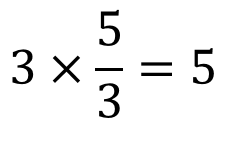
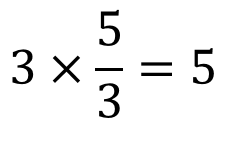
よって
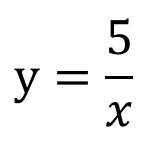
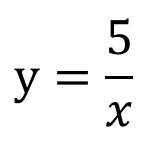
分数が出てきても余裕でしたね!
おそらく分数は約分で消えてしまう問題しか出てきませんので、あまり難しく考えないでくださいね^^
次はグラフから読み取る練習問題
どうぞっ!
問題
次のグラフを式にしなさい。
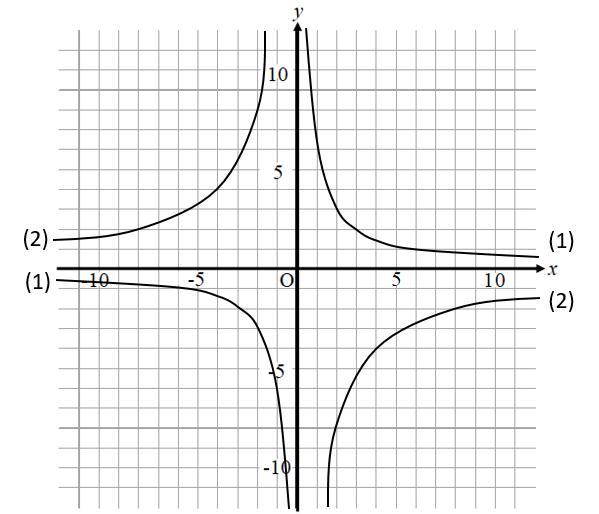

それでは(1)の解説
グラフから座用を読み取りましょう。
なるべく原点近くの座標を見つけると
(1,6)という点が見つかりますね!
というわけでxの値とyの値を掛けてやると
1×6=6
比例定数が求まったので
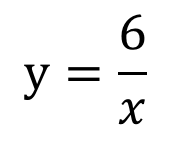
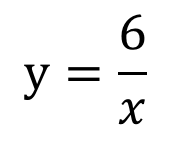
ですね!
ラスト(2)の解説!
こちらもさっきと同様
原点に近い座標を読み取ります。
すると(2,-8)という点が見つかりました。
xとyの値を掛けてやって
2×(-8)=-16
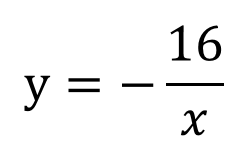
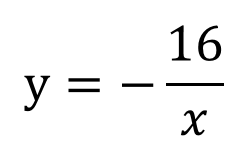
となりました!
練習問題終わり!
これくらいの問題が理解できれば、反比例の式を作るのは余裕だと思います。
正直簡単だなーって思われたかとも多いと思いますが
これと同等の問題が入試に出題されることもあります。
ちゃんとやり方を覚えていればラッキー問題ですよね♪
絶対に覚えておきましょう!
以上、反比例の式の作り方(aを求める)方法についての解説でした。
比例の式の作り方に関してはこちらをどうぞ!
反比例の式を作る簡単な方法を解説!←今回の記事




















わかりやすい!
ありがとうありがとうございます、
嬉しいコメントありがとうございます(^^)
少しでもお役に立てたのであれば幸いです!