反比例のときって
変化の割合は一定だっけ？
そもそも変化の割合の求め方ってどうだっけ？
今回の記事では、反比例の変化の割合について解説していきます。
今回の記事は、こちらの動画でも解説しています(/・ω・)/
変化の割合の求め方とは？
変化の割合の求め方は
こうでしたね！
この求め方は
比例だろうが反比例だろうが一次関数や二次関数においても
どんな関数でも求め方は同じです。
反比例の変化の割合を求める
それでは、実際に反比例の変化の割合を求めてみます。
問題
関数\(y=\frac{8}{x}\)について、\(x\)が次のように増加するときの変化の割合を求めなさい。
（1）2から4
（2）－8から－4
それでは(1)から解説していきます。
変化の割合を求めるためには
x、yそれぞれの増加量を求める必要があります。
そのため、対応表を書いて増加量を調べていきます。
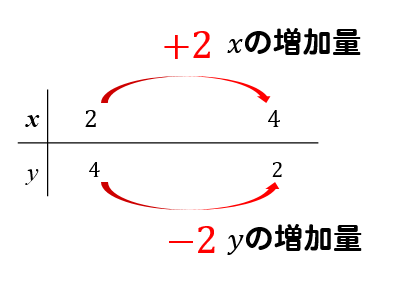
対応表から
xの増加量は＋2
yの増加量はー2
つまり、変化の割合は\(\frac{-2}{2}=-1\)となります。
では（2）も同様に求めてみましょう。
対応表を作って増加量を調べると
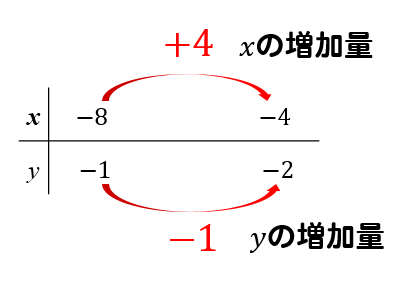
xの増加量は＋4
yの増加量は－1
つまり、変化の割合は\(-\frac{1}{4}\)となります。
xが2から4まで増加するときの変化の割合は－1
xが－8から－4まで増加するときの変化の割合は\(-\frac{1}{4}\)
ということがわかりました。
ここからわかることは
xの値によって、変化の割合は異なる。
反比例のとき
変化の割合は一定ではない！
ということですね。
これで、結論は出たわけなんですが
応用力を高めたいあなたは
もう少し踏み込んで考えてみましょう。
そもそも、変化の割合ってどんなもの？
変化の割合をグラフでイメージしてみる
変化の割合というのは
指定した範囲で、グラフがどのくらいの変化をしているか？
を表わす数です。
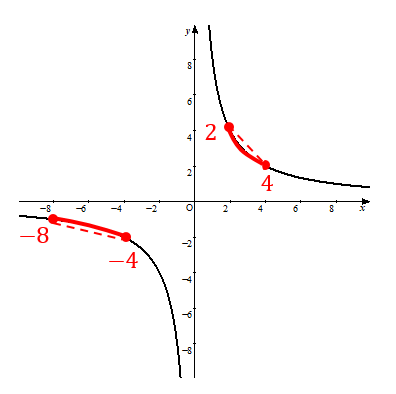
つまり、さっきの反比例のグラフで見てみると
－8から－4の部分では少し緩やかに下がっているのに対して
2から4の部分ではちょっと急に下がっていますよね。
反比例のグラフでは
緩やかに変化している場所もあれば
急激に変化している場所もある
ということで変化は一定ではないので
変化の割合も一定ではないということになります。
それに対して
比例、一次関数のグラフは直線なので
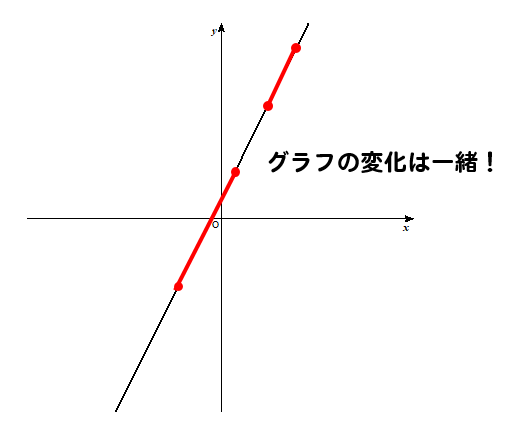
どこの部分を見ても
変化は一定です。
ということで変化の割合は一定ということになります。
あ、2乗に比例するグラフは
もちろん変化の割合は一定ではないからね！
だって、放物線って
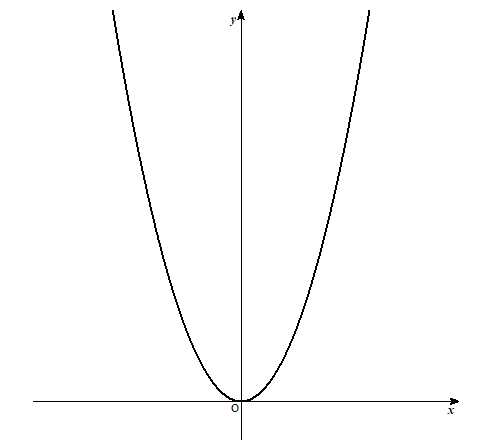
ぐねってるもんね。
原点付近では変化少ないけど
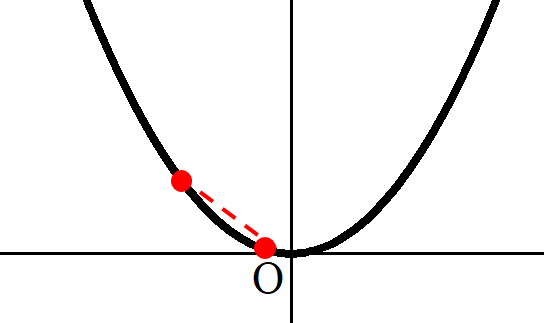
原点から離れていくと、めっちゃ変化してる！！！
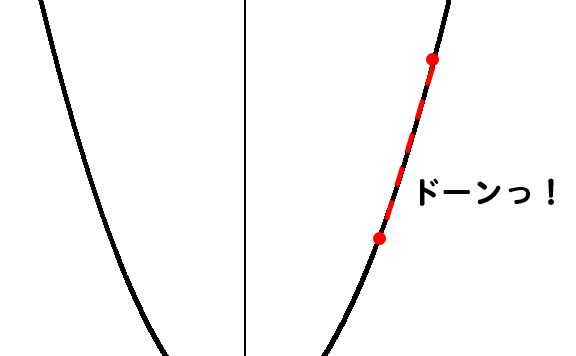
というわけで
変化の割合っていうのは
グラフがどれくらい変化しているかを表している
っていうことをしっかりとイメージしてもらえると
変化の割合は一定？一定ではない？
という疑問を解決することができるはずです(^^)
変化の割合が一定
- 比例（直線）
- 一次関数（直線）
変化の割合が一定ではない
- 反比例（双曲線）
- 2乗に比例する関数（放物線）
数スタのオリジナル教材を販売中！
数スタのオリジナル教材を作成しました。
第1弾は高校入試対策、規則性の教材です。
苦手にしている人が多い単元ですが、
コツを掴むと簡単に解けるようになります。
⇒ 【高校入試】規則性の問題をゼロから＋10点する教材
