【反比例の公式】中学数学で覚えておきたい公式は？

反比例の単元では、覚えておきたい公式はそんなに多くありません。

覚えておきたいものとしては、以下の３つ！

それぞれの項目において、どんな公式があったかを確認していきましょう。

反比例の公式【特徴】

まず、反比例とは何か？について確認しておきましょう。

反比例とは

のことをいいます。

具体例を挙げてみます。

このときの\(x\)と\(y\)の関係を表で表すと

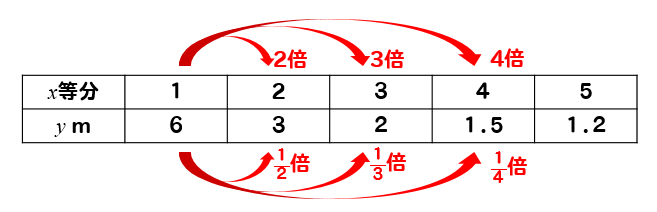
このように、\(x\)を2倍、3倍…すると

\(y\)の方は、\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍…となっていることがわかるよね。

このような関係になっているとき、\(y\)は\(x\)に反比例するというよ。

更に、先ほどの表をもう少し深堀してみると…

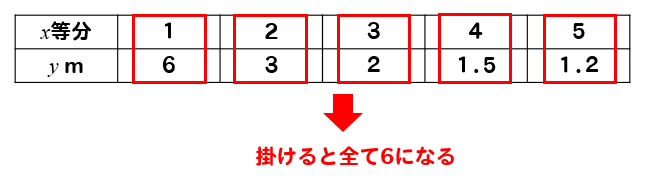
このように、上下の値を掛けるとすべて同じ値になっていることが分かるよね。

これもまた反比例の特徴です。

反比例の関係にあるとき、\(x\)と\(y\)の値は掛け算すると常に同じ値になります。

これを公式っぽく表したものが次の式です。

反比例は、\(x\)と\(y\)の値を掛けると同じ値になり、そのときに出てくる値のことを比例定数といいます。

反比例定数ではないからね！

間違えないよう、覚えておきましょう。

反比例の公式【式の作り方】

次は、反比例の式を作るときに覚えておきたい公式を確認していきましょう。

関数の式を表すときには、\(y=\cdots\)  という形で表すのが一般的です。

そこで、先ほど確認した反比例の公式 \(xy=a\) を思い出してください。

この式を、\(y=\cdots\) となるよう変形すると次のようになります。

$$\begin{eqnarray}xy &=& a \\ y &=& a\div x\\ y&=&\frac{a}{x} \end{eqnarray}$$

これを反比例の式を作るための公式として利用していきます。

使い方は、とってもシンプル！

代入するだけです。

では、具体例を見てみましょう。

\(y=\frac{a}{x}\) に \(x=2\) と \(y=4\) を代入すると

$$\begin{eqnarray} 4&=&\frac{a}{2} \\ 4\times 2 &=& a\\ a &=& 8\end{eqnarray}$$

よって、反比例の式は

$$y=\frac{8}{x}$$

となります。

反比例の公式【グラフ】

反比例のグラフを書く上で、特別な公式はありません。

頑張って書く！

というのが反比例の特徴です。

詳しくはこちらの記事で解説していますが

＞反比例のグラフの書き方を基礎からていねいにやってみよう！

点を１つずつ書いて、なめらかな線で結ぶだけ！

覚えておきたい点としては

グラフが双曲線になるということ。

たまーに、グラフの名前を問われることもあるので覚えておきたいところです。

また、グラフから式を求めろ！という問題もあります。

これまた楽勝です。

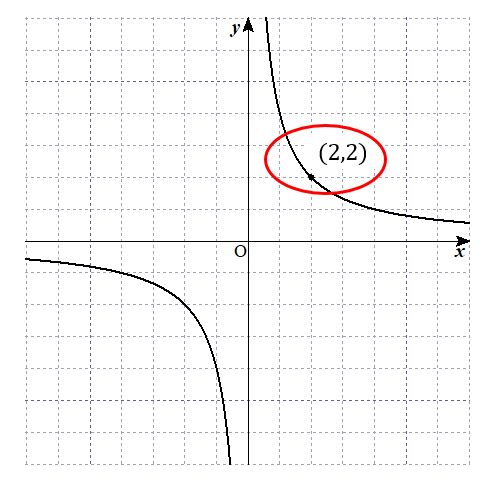
グラフ上から、ぴったりと座標がともに整数になっているところを読み取ります。

上のグラフであれば、例として \((2,2)\) というのが読み取れますね。

この座標は、\(x=2\) のとき \(y=2\) だということを表しています。

なので、先ほど確認した式の作り方を利用すれば解くことができます。

\(y=\frac{a}{x}\) に \(x=2\) と \(y=2\) を代入すると

$$\begin{eqnarray} 2&=&\frac{a}{2} \\ 2\times 2 &=& a\\ a &=& 4\end{eqnarray}$$

よって、反比例の式は

$$y=\frac{4}{x}$$

となります。

グラフから式を求める方法についてはこちらの記事でも解説しています。

＞反比例のグラフの書き方と読み取り方を解説！

反比例の公式【歯車】

反比例の利用問題では、歯車を扱うことがあります。

例えば、次のような問題です。

これはちょっと知識を持っていないと難しい問題ですね…

覚えておきたい公式としてはこれ！

この公式を覚えておけば、簡単に解くことができます。

$$（Aの歯数）\times （Aの回転数）=（Bの歯数）\times （Bの回転数）$$

$$45\times 8=x\times y$$

$$360=xy$$

$$y=\frac{360}{x}$$

このように求めることができます。

反比例の公式【まとめ】

以上！中学数学で学ぶ反比例の公式についてでした。

利用問題においては、他にもあるといえばあるのですが

公式としてまとめておくほどのものではないので割愛させていただきました。

反比例の単元では、公式といえるようなものは多くありません。

覚えておきたいのは今回紹介した

これくらいですね。

これらを覚えておけば、大体の問題は解けると思います(^^)

あとは、たくさん問題を解いて理解を深めていきましょう！