高校数学Ⅰで学習する集合の単元から
「集合の要素の決定」
についての問題をいくつか例題をあげながら解説していきます。
要素の決定についてはこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
【例題①】集合の要素の決定
【問題】ニューアクションβより
\(a,b\)を自然数とする。次の2つの集合A,Bに対して次の問いに答えよ。
\(A=\{1, 3a+1, 2b\}\)
\(B=\{a+1, b-1, 2a+2b, 5a+b\}\)
(1)\(A\subset B\) となるような、\(a,b\)の値を求めよ。
(2)\(A\cap B=\{4, 10\}\) となるような、\(a,b\)の値を求めよ。
\(a,b\)はそれぞれ自然数(正の整数)であることから、
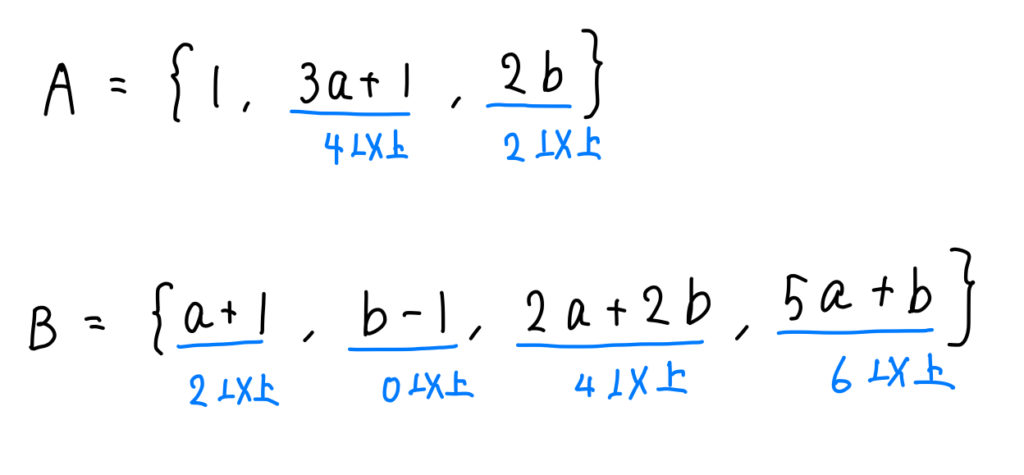
このように、A,Bの要素の範囲が分かりますね。
このことを踏まえた上で各問を考えていきましょう。
(1)
\(A\subset B\) となるというのは、
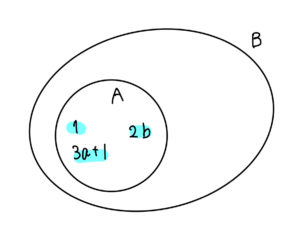
このようにAの要素がすべて、Bの集合に含まれているということを指します。
ということは、Aの要素である1はBに含まれることになります。
では、Bの要素のうちどれが1になるのでしょうか。
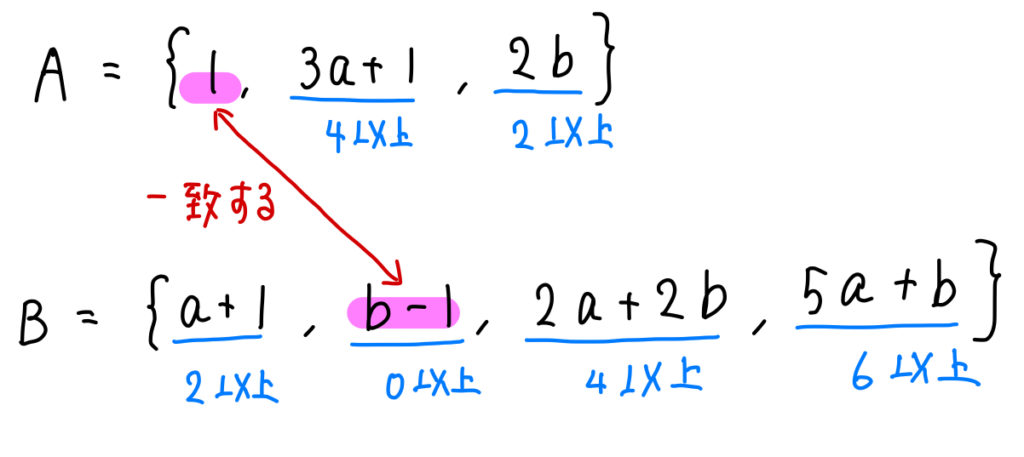
それは問題を解く前に考えた範囲から明らかになります。
\(a+1\)は2以上、\(2a+2b\)は4以上、\(5a+b\)は6以上。
なので、1になることができるのは \(b-1\) しかありません。
よって、\(b-1=1 ⇒ b=2\) となります。
では、\(b=2\) ということから
\(A=\{1, 3a+1, 4\}\), \(B=\{a+1,1,2a+4,5a+2\}\)
になるので、ここから\(a\)の値を求めていきましょう。
ここで明らかになったAの要素4、これもBに含まれることになります。
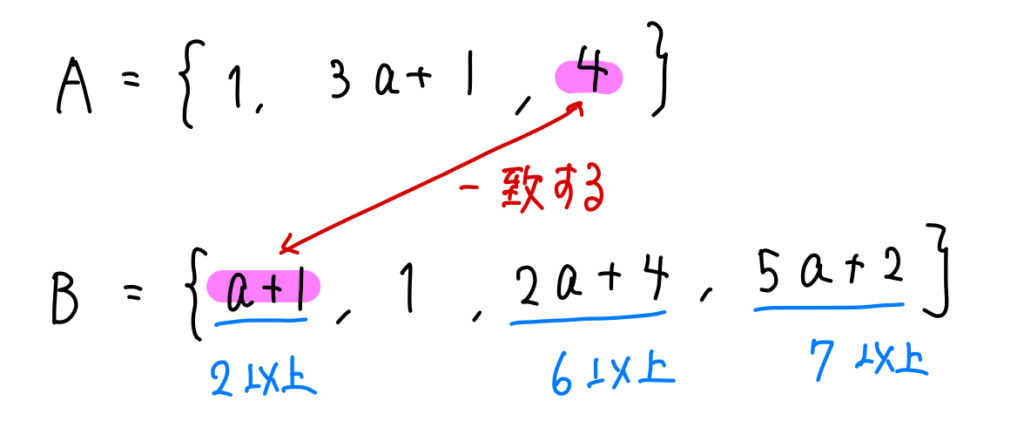
すると、Bの要素の中で4と一致するのは \(a+1\) であることが分かります。
よって、\(a+1=4 ⇒ a=3\) となります。
ここまでで、\(a=3,b=2\) であることが分かりましたが、
これが問題の条件を満たしているかどうかを確かめてみましょう。
\(a=3,b=2\)のとき、
\(A=\{1, 4, 10\}\), \(B=\{1, 4, 10, 17\}\) となり、
\(A\subset B\) が成り立っていることが確かめられますね!
よって、
$$\color{red}{(1) a=3,b=2 \cdots(解)}$$
(2)
\(A\cap B=\{4, 10\}\) となるというのは、
AとBの共通している要素が4、10であるということです。
このことから、

Aには4と10という要素が含まれており、
\(3a+1,2b\) のどちらかが4と10になるということが読み取れます。
ここで、\(3a+1=4, 2b=10\)のとき、\(3a+1=10, 2b=4\)のときで場合分けして話を進めていきます。
\(3a+1=4, 2b=10\)のとき、\(a=1,b=5\) となります。
このとき、AとBの要素を見ると
\(A=\{1, 4, 10\}\), \(B=\{2, 4, 10, 12\}\) であるから、
\(A\cap B=\{4, 10\}\) を満たしていることが分かります。
\(3a+1=10, 2b=4\)のとき、\(a=3,b=2\) となります。
このとき、AとBの要素を見ると
\(A=\{1, 4, 10\}\), \(B=\{1, 4, 10, 17\}\) であるから、
\(A\cap B=\{1, 4, 10\}\) となってしまい、
1が余分に含まれているため、問題の条件を満たさなくなってしまいます。
なので、\(a=3,b=2\)は不適ということになりますね。
以上のことより
$$\color{red}{(2) a=1,b=5 \cdots(解)}$$
【例題②】集合の要素の決定
【問題】
\(A=\{3,a,2a+1\}\) , \(B=\{5,6,3a-3\}\) ,\(A\cap B=\{3,5\}\) のとき、定数\(a\)の値と和集合\(A\cup B\)を求めよ。
\(A\cap B=\{3,5\}\)ということから、
Bの要素である \(3a-3\) は\(3\)であることが確定します。
\(3a-3=3 ⇒ \color{red}{ a=2 \cdots(解)}\)
よって、AとBの集合は次のように表せます。
\(A=\{2, 3, 5\}\), \(B=\{3, 5, 6\}\)
以上より、和集合は
$$\color{red}{A\cup B=\{2,3,5,6\}\cdots(解)}$$
となります。
【例題③】集合の要素の決定
【問題】
実数\(a\)に対して、2つの集合
\(A=\{a-1,4,a^2-5a+6\}\)、\(B=\{1,a^2-4,a^2-7a+12,4\}\)
とする。\(A\cap B=\{0,4\}\)であるとき、\(a\)の値を求めよ。
\(A\cap B=\{0,4\}\)ということから、
Aの要素である、\(a-1\),\(a^2-5a+6\) のどちらかが0になることが分かります。
このとき、Bの要素に注目してもいいんだけど、
Aの要素の方が次数が低いこともあって利用しやすいです。
では、\(a-1=0\),\(a^2-5a+6=0\) のときで場合分けをしながら話を進めていきましょう。
\(a-1=0\) のとき、\(a=1\)であり、
\(A=\{0, 2, 4\}\), \(B=\{-3, 1, 4,6\}\) となります。
このとき、\(A\cap B=\{4\}\) となってしまい、条件を満たしません。
よって、\(a=1\) は不適。
\(a^2-5a+6=0\) のとき、\(a=2,3\)となります。
まず、\(a=2\) のとき
\(A=\{0, 1, 4\}\), \(B=\{0, 1, 2,4\}\) となります。
このとき、\(A\cap B=\{0,1,4\}\) となってしまい、条件を満たしません。
よって、\(a=2\) は不適。
次に、\(a=3\) のとき
\(A=\{0, 2, 4\}\), \(B=\{0, 1,4,5\}\) となります。
このとき、\(A\cap B=\{0,4\}\) となるから条件を満たしています。
よって、\(a=3\) はOKとなります。
以上のことをまとめると、
$$\color{red}{a=3\cdots(解)}$$
まとめ!
お疲れ様でした!
質問が多い問題をピックアップして紹介してみました。
与えられた条件から、
要素の値を絞り込んでいくっていうのがポイントですね。
あとは、値が求まった後に
ちゃんと集合の要素を書き出してみて、
条件を満たしているかどうかをチェックすること。
これも大事な過程になるのでお忘れなく(/・ω・)/















コメントを残す