今回は中3で学習する
『相似な図形』の単元から
図形の体積比について解説していくよ!
円錐の図形を

このように、2つに分けたとき
体積比はそれぞれどうなるのかな?
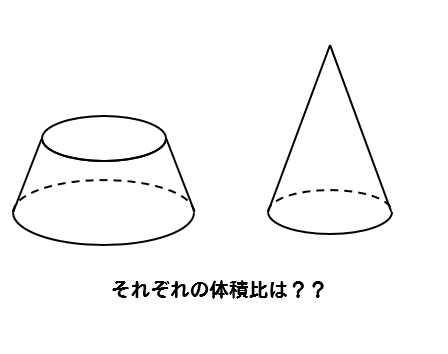
ということについて問題を使って解説をしていきます。
相似な立体の体積比は
まず、体積比の問題を考えるときに
知っておきたいことがコレ!
相似な立体の体積比は
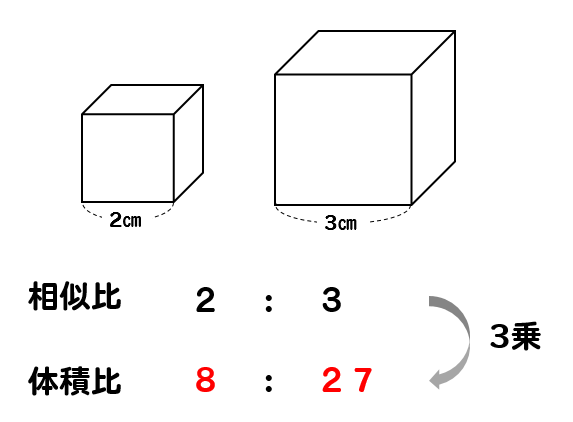
相似比を3乗することで求めてやることができます。
つまり
相似比がわかれば
体積比はすーぐに求めることができるということですね!
それでは、さっきの円錐の問題を考えてみましょう。
円錐問題の考え方
円錐を2つに分けた図形の体積比を考えるのですが

そもそも相似になっていません…
では、どのように考えていけば良いのかというと
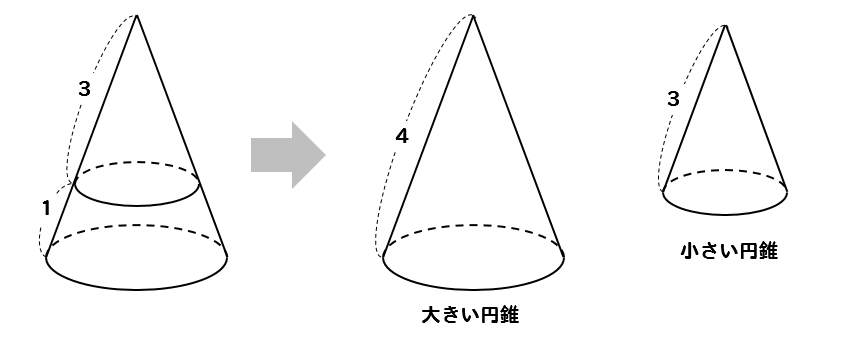
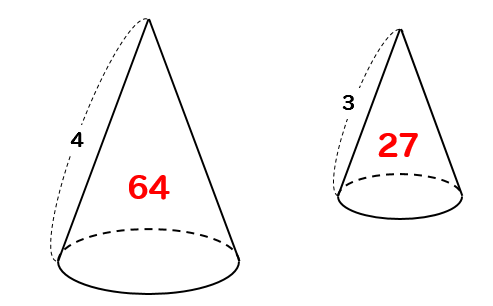
一旦、このように小さな円錐と大きな円錐を考えてやります。
大きい方の円錐は③と①を合わせた辺になっているから④になるっていうのはOKだね。
そうすると2つの立体は相似になっているので
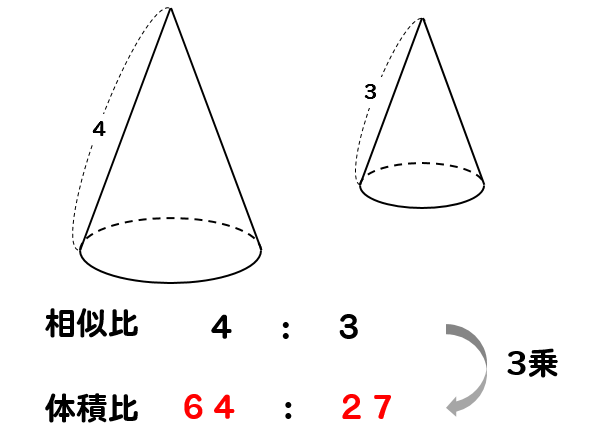
相似比が\(4:3\)になることから
それぞれを3乗した値を考えて
体積比は\(64:27\)となります。
ここから
円錐の土台部分となる立体の体積はどうなっているのかを考えていきます。
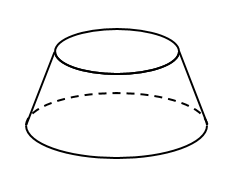
この土台部分の立体は
大きな円錐から小さな円錐を取り除いた部分と考えることができるよね。
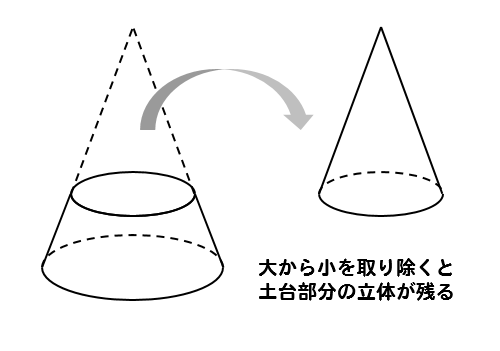
だから、土台部分の体積は

先ほど求めた大きい円錐と小さい円錐の体積比の数を用いて
$$64-27=37$$
と求めてやることができます。
よって、問題で聞かれていた

小さい円錐と土台部分の体積比は?
という問いの答えは
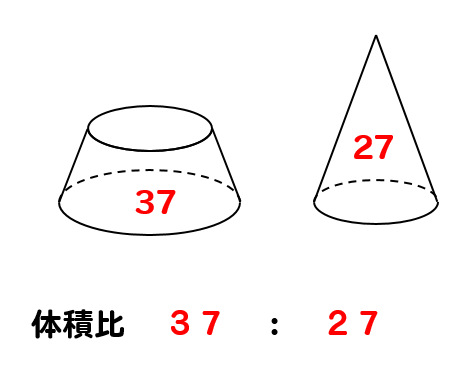
このように\(37:27\)と求めてやることができました。
円錐を切り取って体積比を考えるような問題では
比較する立体が相似でなくても
このように相似な立体を見つけて、不要な部分を取り除いたりしながら考えると答えを求めることができます。
それでは、他にも円錐の体積に関する問題に挑戦して
理解を深めていきましょう!

演習問題に挑戦しよう!
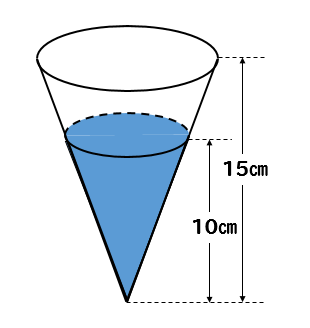
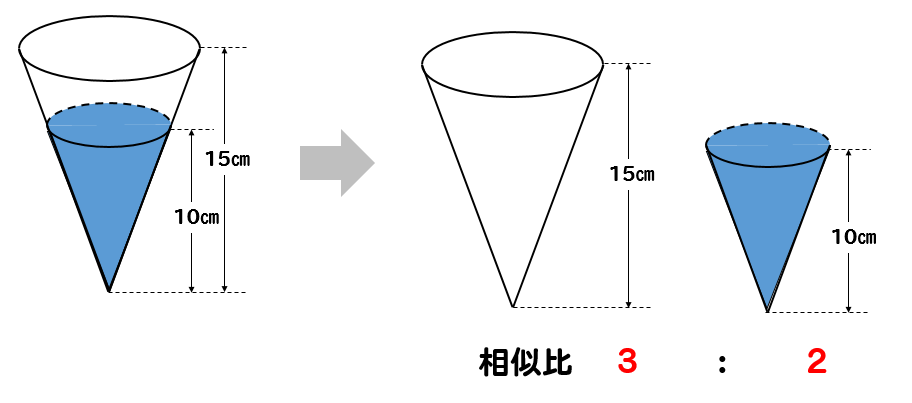
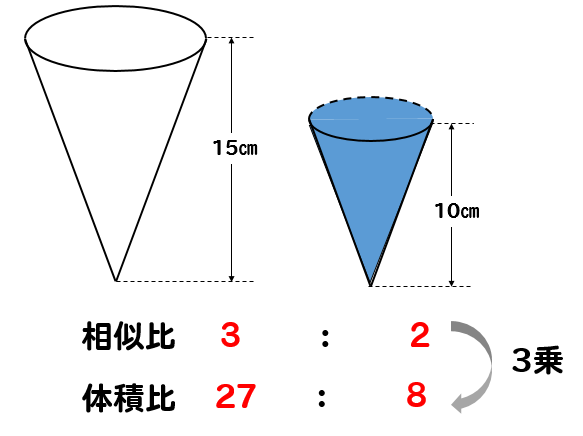
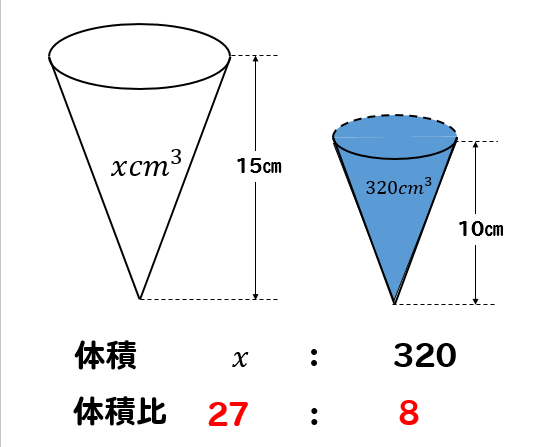
下の図のような円錐形の容器に320cm³の水を入れ、水面と容器の上の面が平行になるようにして深さを測ると、10㎝になった。水はあと何cm³入るか求めなさい。
円錐の体積比 まとめ
お疲れ様でした!
円錐の体積比を考える問題では
まず、相似になっている立体を見つけるようにしましょう!

そうすれば、相似比から体積比を求めることができます。
あとは問題によって

このように立体を取り除いたりしながら
求めたい部分の体積比を求めていけばOKです。
ちょっと難しそうに見える問題ですが
一度解いてしまえば考え方は簡単な問題です(^^)
しっかりと練習して、必ず解けるようにしておこうね!
ファイトだー(/・ω・)/
円錐の体積比を解説!←今回の記事


















ありがとうございます!
分かりやすかったです!