今回は、中3で学習する
『相似な図形』の基本にあたる
相似な図形の性質について解説していきます！
- 相似ってなに？
- 相似だとどんなことが分かるの？
- どんな問題が出るの？
という視点で、話を進めていきますね。
では、いきましょー！
Contents
相似ってなに？
拡大、縮小の関係にある図形のことを相似(そうじ)といいます。
こっちの掃除(そうじ)じゃないからね
相似！
拡大、縮小の関係にあるというのはどういうことかというと
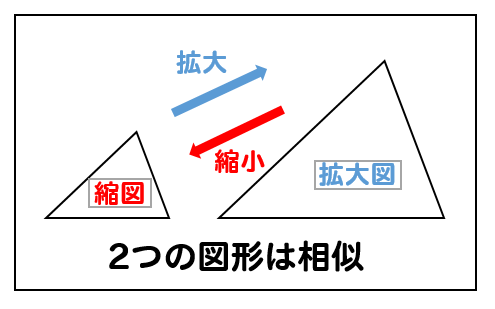
一方の図形を
形を変えずに大きく(拡大)
形を変えずに小さく(縮小)した図形を
『2つの図形は相似である』といいます。
ちなみに、拡大された図形のことを拡大図
縮小された図形のことを縮図(しゅくず)ということも覚えておきましょう。
縮小図とは言わないから気を付けてね！縮図です。
そして
2つの図形は相似だよー
って伝えたいときには
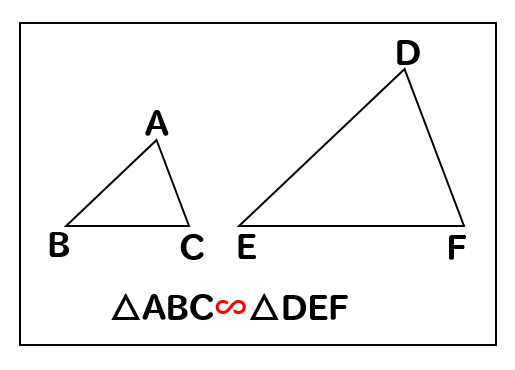
このように記号を使って表します。
相似な図形の性質
相似な図形というのは
拡大、縮小の関係にある図形のことだと分かりましたね。
それでは、拡大縮小という特徴を押さえつつ
相似である図形には、どんな性質があるのか見ていきましょう！
対応する辺の長さの比は、すべて等しい
相似な図形では、対応する辺の長さの比が全て等しくなります。
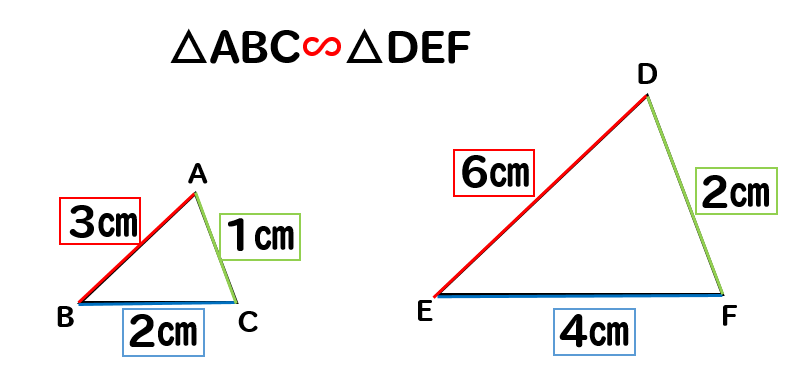
『対応する辺』というのは
同じ色を付けたところどうし
ABとDE、BCとEF、CAとFD
のように同じ部分の辺のことを言います。
そして、相似な図形の場合
この対応する辺どうしの長さを比で比べてみると
AB：DE＝3：6＝1：2
BC：EF＝2：4＝1：2
CA：FD＝1：2
すべて同じ！！
そして
対応する辺の長さの比のことを
2つの図形の相似比といいます。
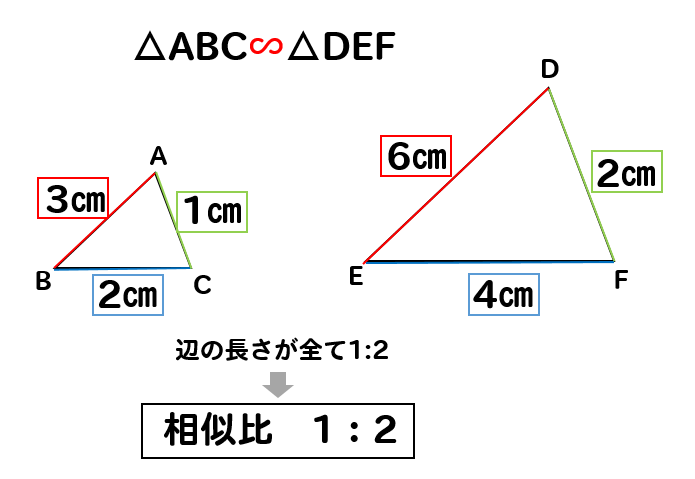
『対応する辺の長さの比がすべて等しい』
この性質を知っておくと
こんなことができるようになります。
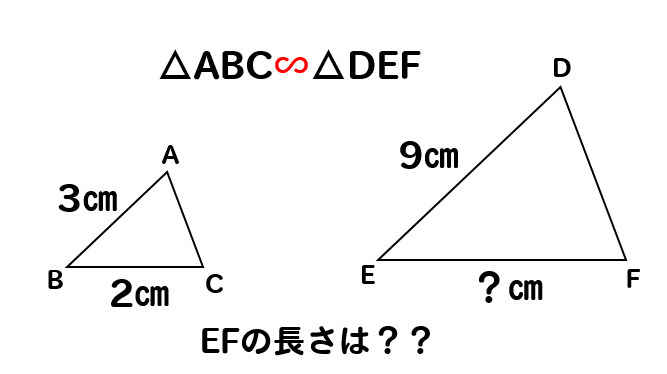
辺の長さを求めることができる！！
ABとDEの長さを比べると
この図形の相似比は1：3になると分かりますね。
ということは
BCとEFの長さも1：3になる！
このように比を使って、長さを求めることができます。
相似の単元では
比の計算がたくさん出てくるので
計算方法もしっかりと復習しておいてくださいね。
対応する角の大きさは、それぞれ等しい
相似な図形では、対応する角の大きさはそれぞれ等しくなります。
これは単純です。
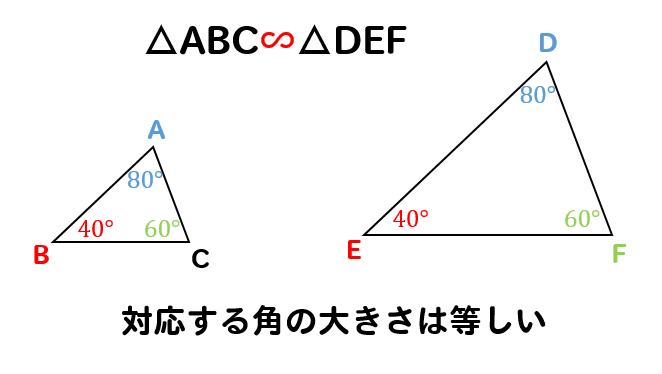
拡大しても、縮小しても
このように対応する部分の
角の大きさは変わりません！
拡大、縮小というのは
形を変えず、図形の大きさを変えることでしたね。
形を変えない ⇒ 角の大きさは変わらない
大きさを変える ⇒ 辺の長さが変わる
という認識を持っておいてください。
- 対応する辺の長さの比は、すべて等しい。
- 対応する角の大きさは、それぞれ等しい。
対応する辺の長さの比を相似比といいます。
基本性質を使った問題
それでは、相似な図形の基本性質を使った問題に取り組んでみましょう。
下の図で、2つの三角形は相似である。このとき、次の問いに答えなさい。
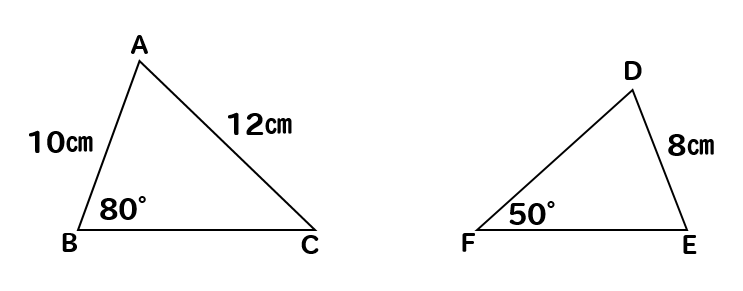
（1）2つの三角形が相似であることを、記号を使って表しなさい。
（2）2つの三角形の相似比を求めなさい。
（3）∠Aの大きさを求めなさい。
（4）辺DFの長さを求めなさい。
それでは、順に解説していきます。
（1）の解説！
（1）2つの三角形が相似であることを、記号を使って表しなさい。
相似の記号∽を使って表していきます。
ちょっと気を付けて欲しいのは
必ず対応する順番になるよう各頂点のアルファベットを書くようにしてください。
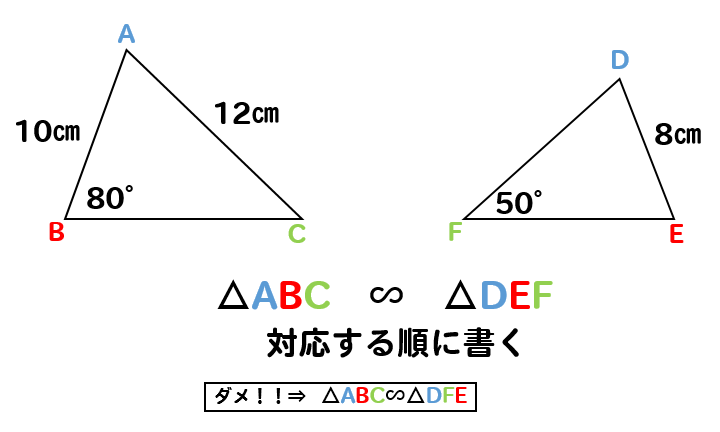
よって、答えは△ABC∽△DEFとなります。
いじわるなことに、図形の向きが変わってたりするので
必ず、どこが対応する点なのかをハッキリさせるようにしてください。
（2）の解説！
（2）2つの三角形の相似比を求めなさい。
対応する辺の中で
長さが分かっているものどうしを比べます。
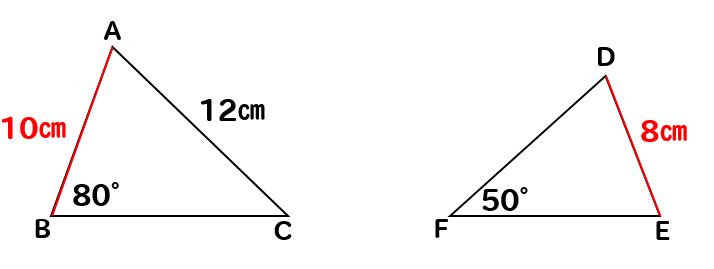
ABとDEの長さを比でとってやると
AB：DE＝10：8＝5：4
よって、相似比は5：4となります。
（3）の解説！
（3）∠Aの大きさを求めなさい。
『対応する角の大きさは等しくなる』
という性質を使って∠Aの大きさを求めていきます。
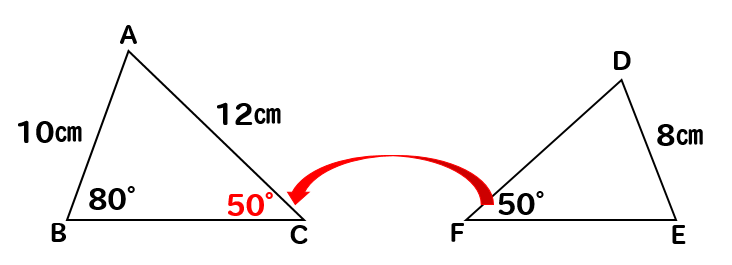
まず、∠Fに対応する∠Cの大きさが50°と分かります。
すると、次は三角形の内角の和に注目して
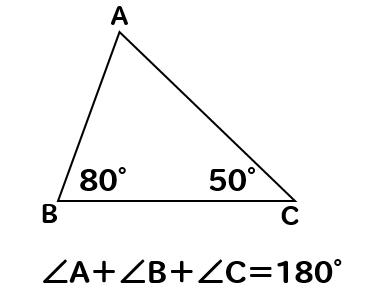
∠A＝180－(80＋50)＝180－130＝50°
よって∠Aの大きさは50°となります。
（4）の解説！
（4）辺DFの長さを求めなさい。
相似比を使って、辺DFの長さを求めていきます。
（2）より相似比が5：4だと分かりましたね。
これより、AC：DFの辺の比も5：4だということになります。
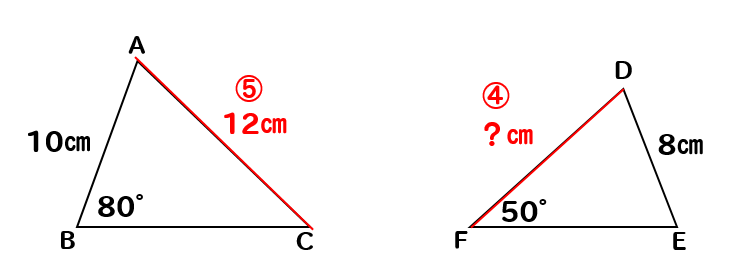
辺DFの長さをxとして、比例式を作ると
よって、辺DFの長さは48/5㎝となりました。
相似の基本性質 まとめ
それでは、最後に簡単なまとめをしておきましょう。
相似な図形とは
拡大、縮小の関係にある図形のことでしたね。
記号を使って、このように表すことができます。
相似な図形の性質とは
- 対応する辺の長さの比は、すべて等しい。
対応する辺の長さの比を相似比といいます。
- 対応する角の大きさは、それぞれ等しい。
以上、相似な図形の基本性質についてでした。
次は
『2つの図形が相似であるかを調べるためにはどうしたらいいの？』
というテーマでお話をしていきます。
相似の単元は入試でも必須だからね！
気合入れてがんばっていきましょう。
ファイトだー！！
相似の基本性質を解説！←今回の記事
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！
数スタのオンラインショップ開設！
⇒ 数スタ STORE
中3受験生向けの演習課題を無料配布中！