今回は中３で学習する相似な図形の単元から
台形と面積比についての問題を解説していくよ！
台形の面積比問題で良く出題されるのが
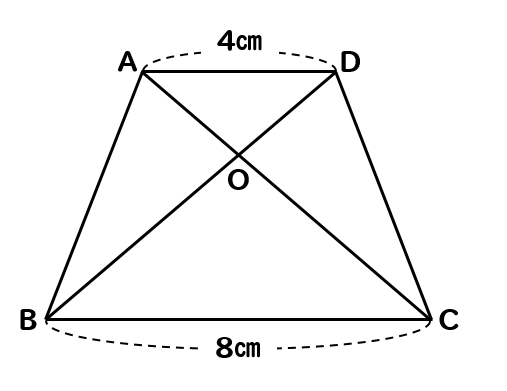こんな形の図形だね。
それでは、この記事を通して
台形の面積比問題をマスターしていこう！
まず知っておきたい面積比のこと
面積比の問題を考えていく上で
とっても大切な面積比の知識を身につけておきましょう。
- 相似な図形において、面積比は相似比の2乗になる
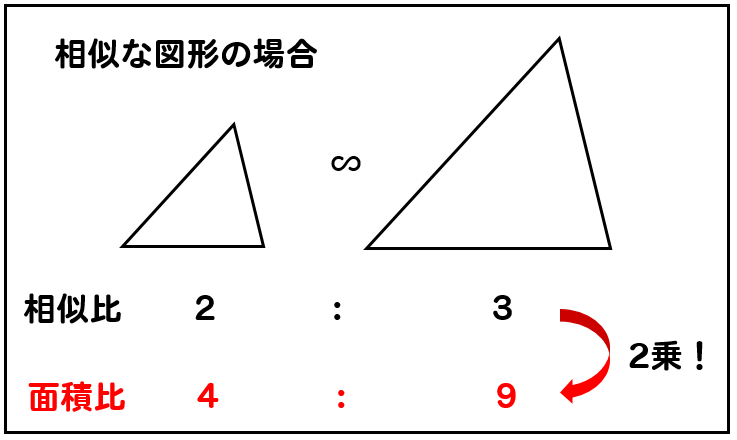
比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。
つまり、台形の中から相似な図形を見つけていくことがポイントになってくるね。
- 相似な図形において、面積比は相似比の2乗になる
比べる三角形が相似でなくても、高さが等しければ
底辺の長さの比が、そのまま面積比となります。
問題を解いていく上で
これら2つの特徴を利用していくことになるから
しっかりと覚えておいてくださいね！
台形の面積比問題を解説！
問題
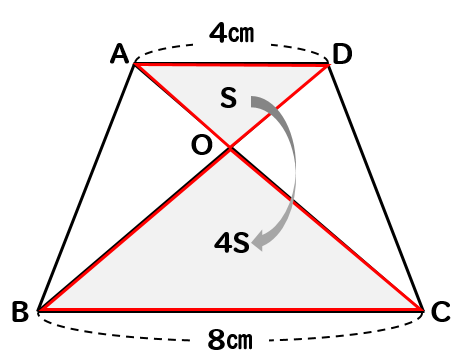
図のような、AD//BCの台形があります。このとき、台形ABCDの面積は△OADの面積の何倍になるか求めなさい。
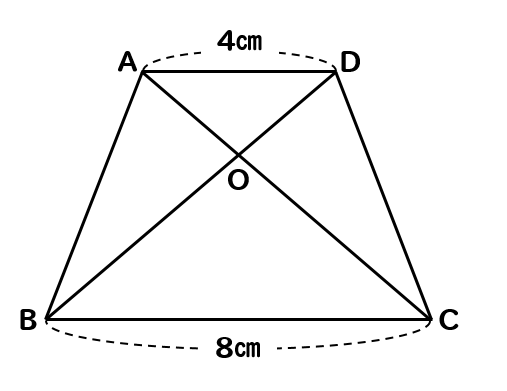
相似な三角形から面積比を考える
まずは基準となっている△OADの面積をSとして考えていきます。
この台形の中から相似な三角形を探していくと
対頂角や錯角が等しくなることから
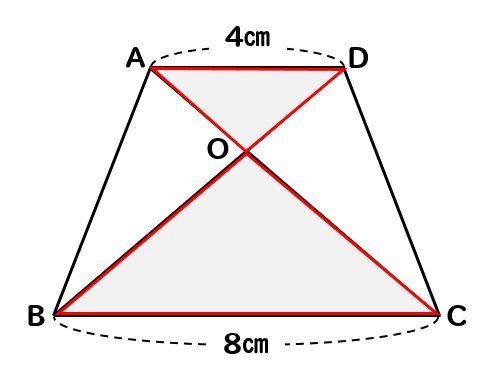
△OADと△OCBが相似になることがわかります。
そして、相似比から面積比を考えていくと
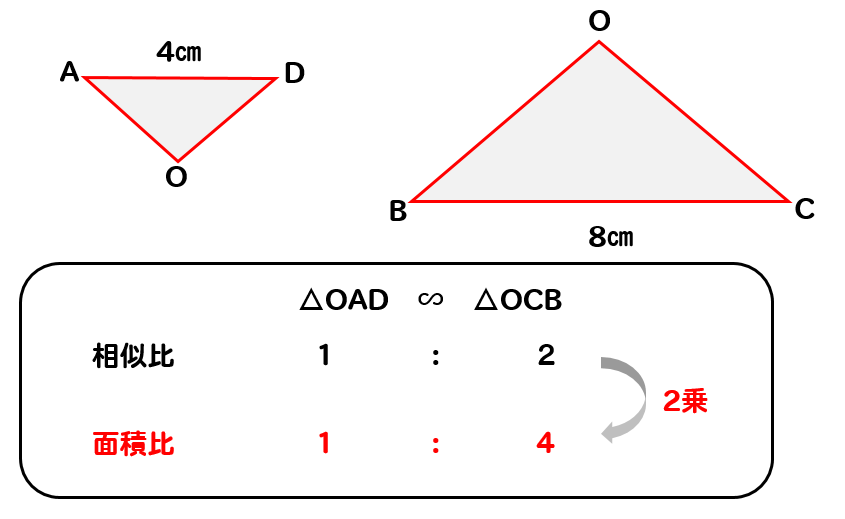
2つの三角形の面積比は１：４であることがわかります。
よって
△OCBの面積は
$$1:4=S:△OCB$$
$$△OCB=4S$$
と表すことができます。
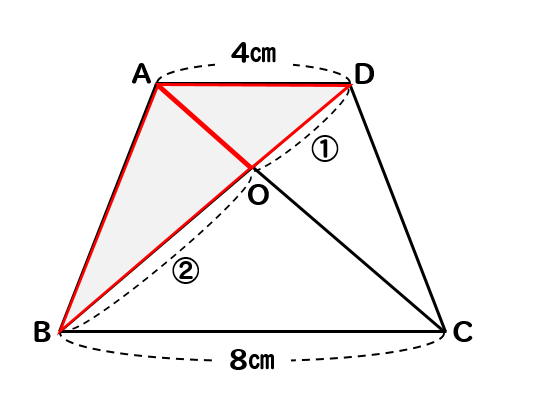
高さの等しい三角形から底辺を見比べて面積比を考える
次に、△OADと△OABに注目していきましょう。
△OAD∽△OCBより
相似比を利用して
$$DO:BO=4:8=1:2$$
ということが読み取れます。
2つの三角形は高さが等しいので
底辺の比がそのまま面積比になります。
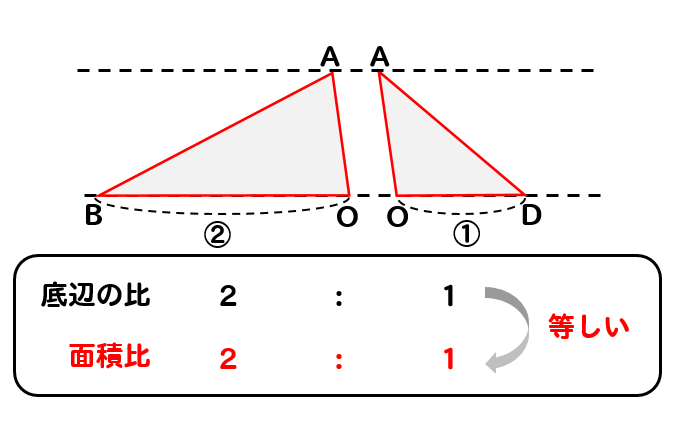
よって
△OABの面積は
$$1:２=S:△OAB$$
$$△OAB=2S$$
と表すことができます。
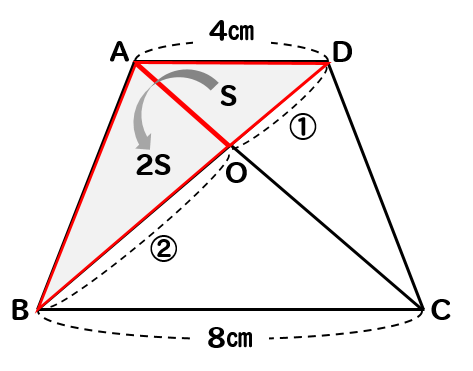
これと同様に
△ODCも2Sと表すことができます。
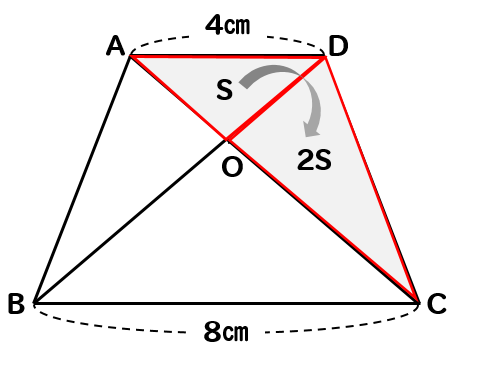
全体を求める
それぞれの三角形をSを使って表すことができました。
それらをまとめると
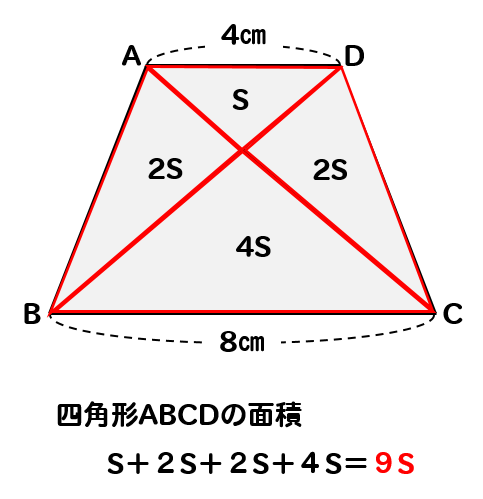
台形の面積は9Sと表すことができました。
よって
$$△OAD=S$$
$$台形ABCD=9S$$
となるので、台形ABCDの面積は△OADの9倍であることが求められました。
台形の面積比ポイント
- 相似な図形から面積比を求める
- 相似比を利用して、底辺の比を比べて面積比を求める
- それぞれを組み合わせて全体を考える
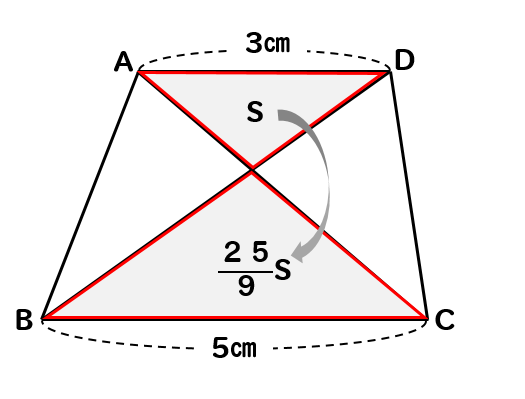
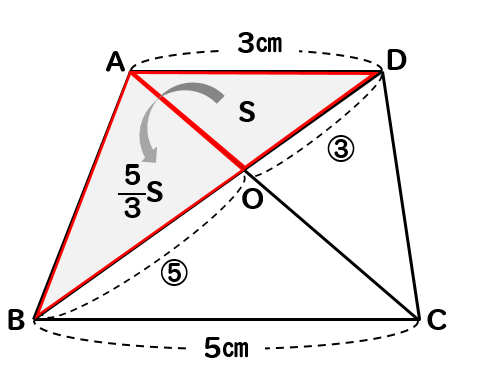
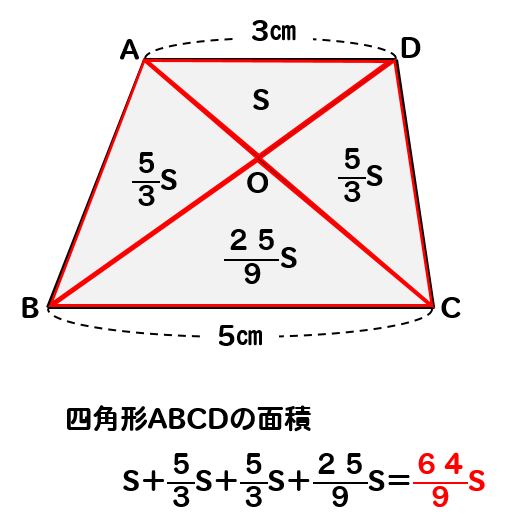
練習問題に挑戦！
それでは練習問題に挑戦して、理解を深めていきましょう。
こちらの問題は計算が、ちょっと複雑になっているので頑張ってね！
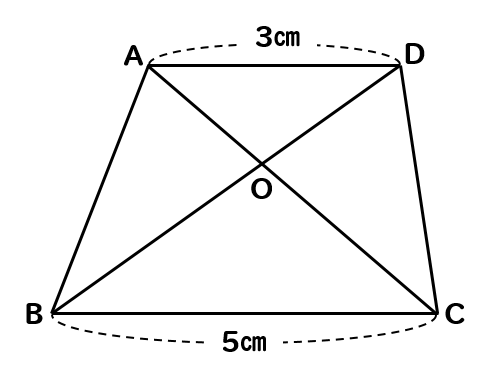
問題
図のような、AD//BCの台形があります。このとき、台形ABCDの面積は△OADの面積の何倍になるか求めなさい。
答え
$$\frac{64}{9}倍$$
まずは△OADの面積をSとして
△OADと△OCBが相似になっていることに注目して面積比を求めていきましょう。
相似比が\(3:5\)だから、面積比は\(9:25\)になりますね。
よって
$$9:25=S:△OCB$$
$$9\times △OCB=25S$$
$$△OCB=\frac{25}{9}S$$
次に、相似比を利用して\(OD:OB=3:5\)ということがわかります。
よって
$$3:5=S:△OAB$$
$$3\times △OAB=5S$$
$$△OAB=\frac{5}{3}S$$
△OCDも同様に求めれるので、まとめて全体を考えると
台形の面積は\(\displaystyle \frac{64}{9}S\)となります。
よって、台形ABCDの面積は△OADの\(\displaystyle \frac{64}{9}\)倍であることが求まりました。
[スタセミ中3バナー]
まとめ
お疲れ様でした！
台形の面積比問題では
相似な三角形や高さの等しい三角形に注目しながら面積比を考えていきます。
だから、これらの特徴はぜーったいに覚えておこうね！
平行四辺形の面積比問題についてはこちらをどうぞ！
面積比！台形の面積比問題を解説！←今回の記事
コメントを残す